【深度学习基础】4. Recurrent Neural Networks
如今深度学习如火如荼,各种工具和平台都已经非常完善。各大训练平台比如 TensorFlow 让我们可以更多的聚焦在网络定义部分,而不需要纠结求导和 Layer 的内部组成。本系列我们来回顾一下深度学习的各个基础环节,包括线性回归,BP 算法的推导,卷积核和 Pooling,循环神经网络,LSTM 的 Memory Block 组成等,全文五篇,前三篇是斯坦福深度学习 wiki 整理,第四第五两篇是 Alex Graves 的论文读书笔记,图片来自网络和论文,有版权问题请联系我们。
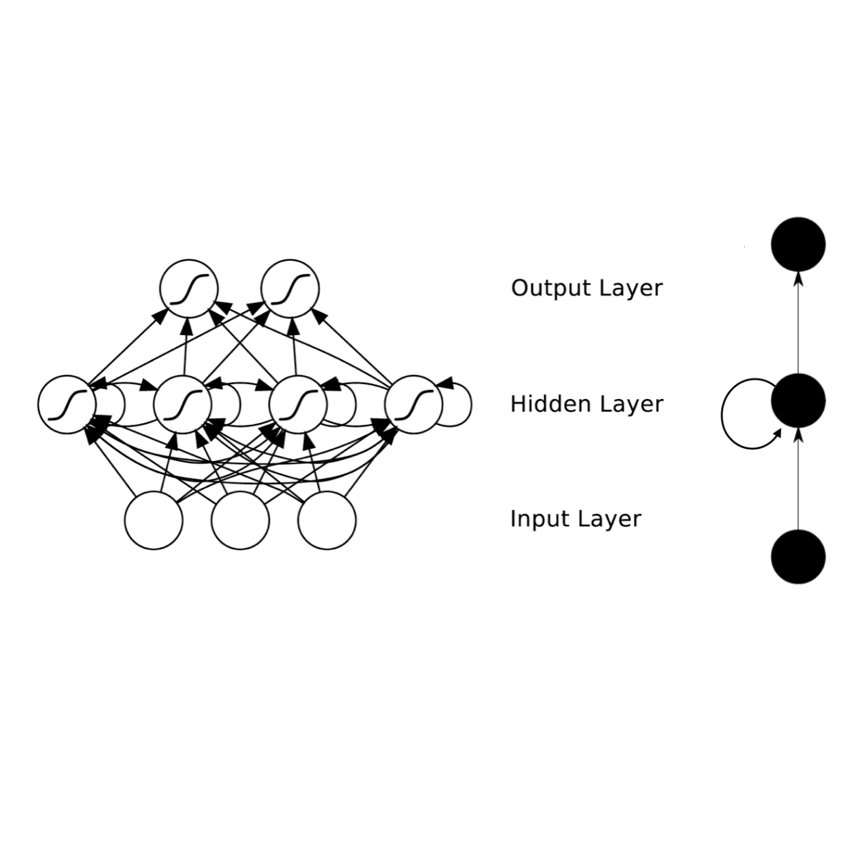
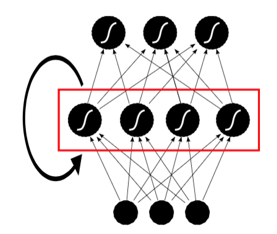
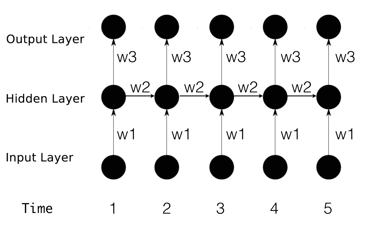
之前已经了解了 ANN,ANN 的网络连接是无环的。如果我们放宽条件,允许节点之间连接形成环,就是 recurrent neural networks(RNNs)。RNN 有许多种实现,我们这里主要关注一种比较简单的,只在隐藏层内自连接的形式,如下图所示:
之前所有类型的多层感知机都是从一个固定维度的 Input 到 output 的映射,而 RNN 可以对整个输入序列的历史进行建模。理论上,如果 RNN 的隐藏节点足够多,他对序列到序列的映射建模是可以做到任意精度的。RNN 通过将序列数据之前的输入“记忆”在网络内,从而达到提高输出精度的效果。
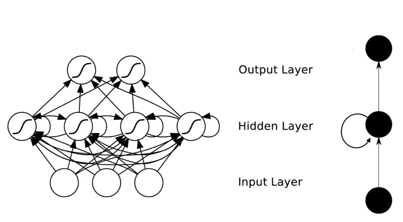
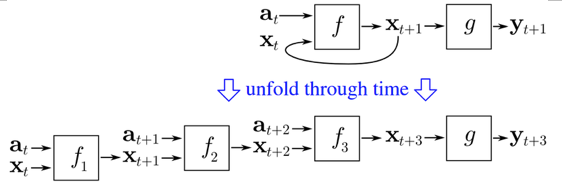
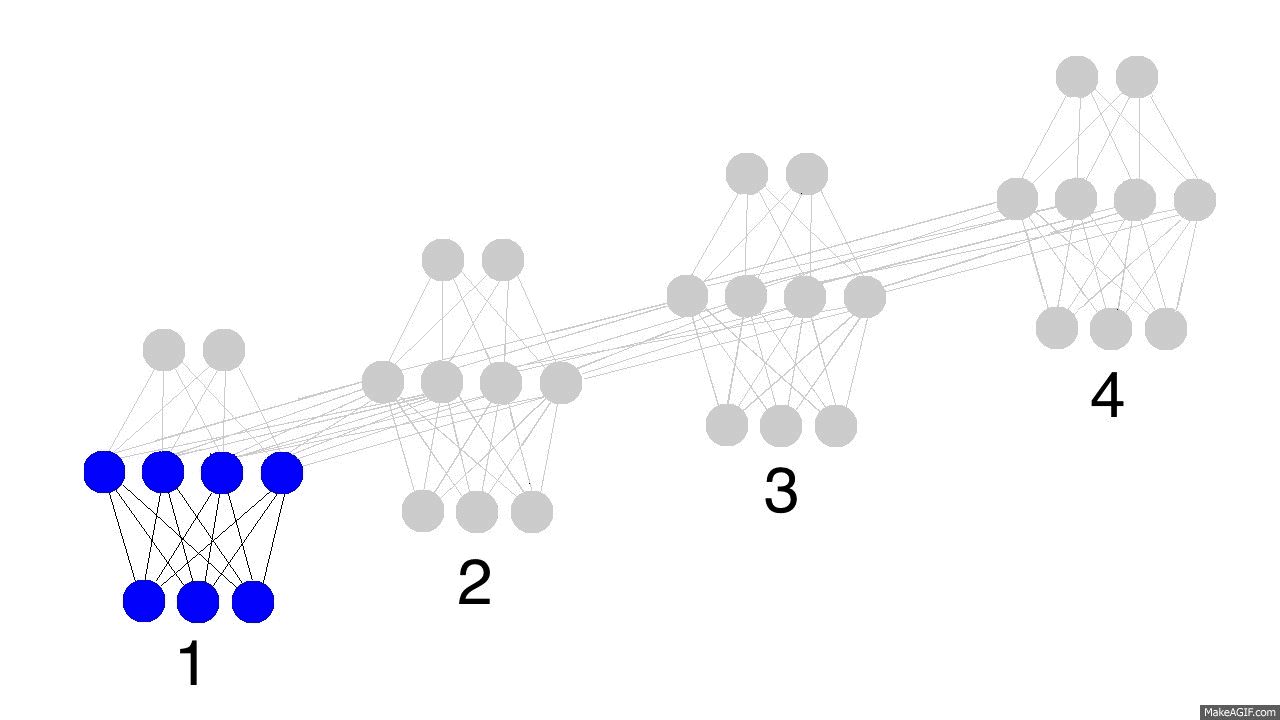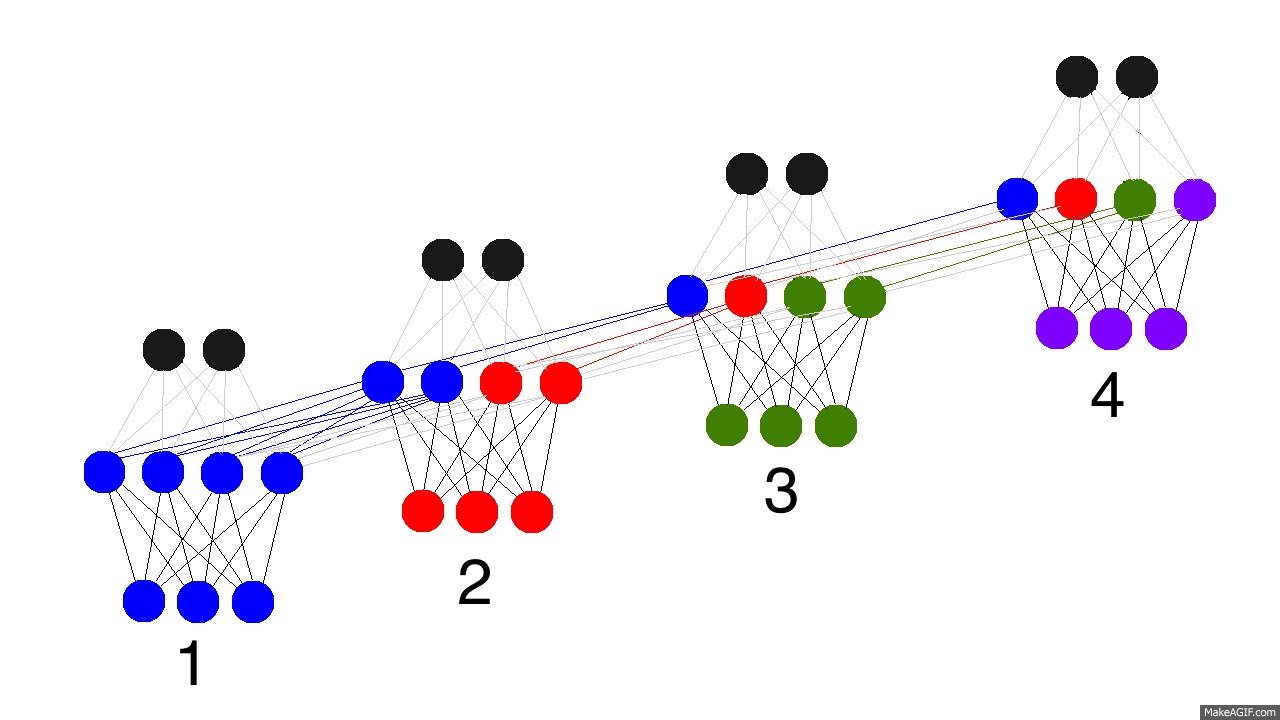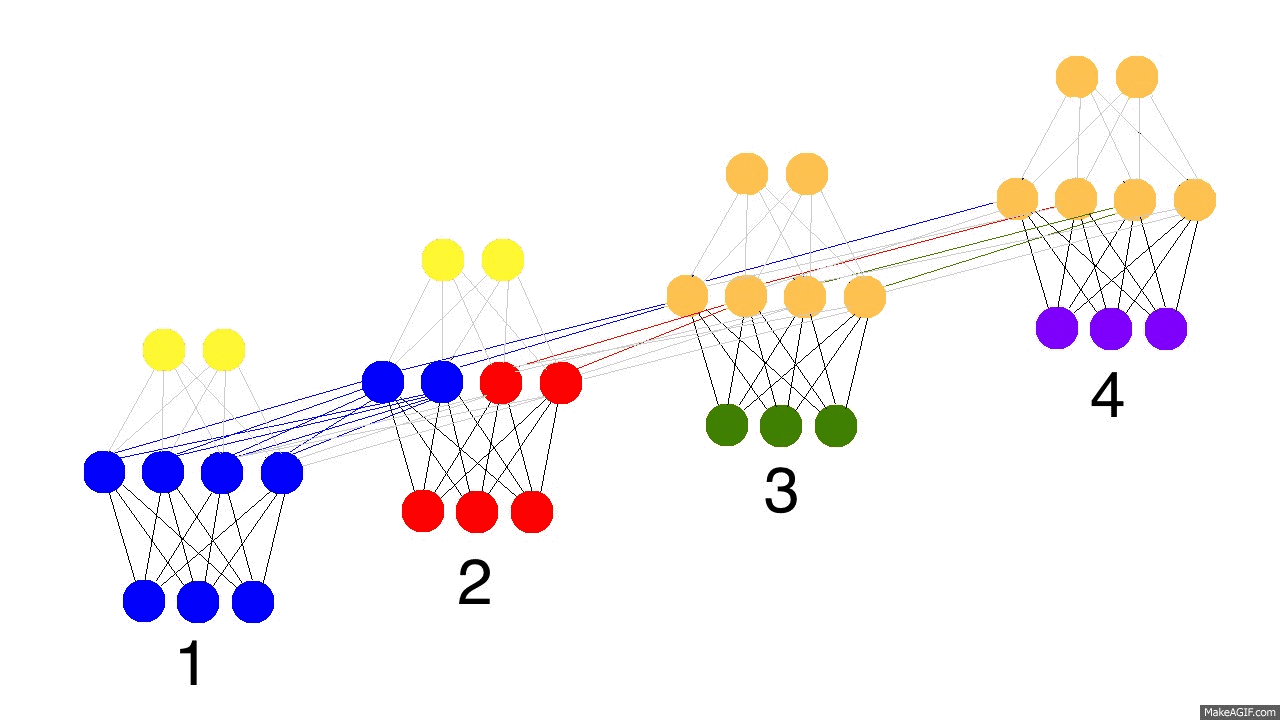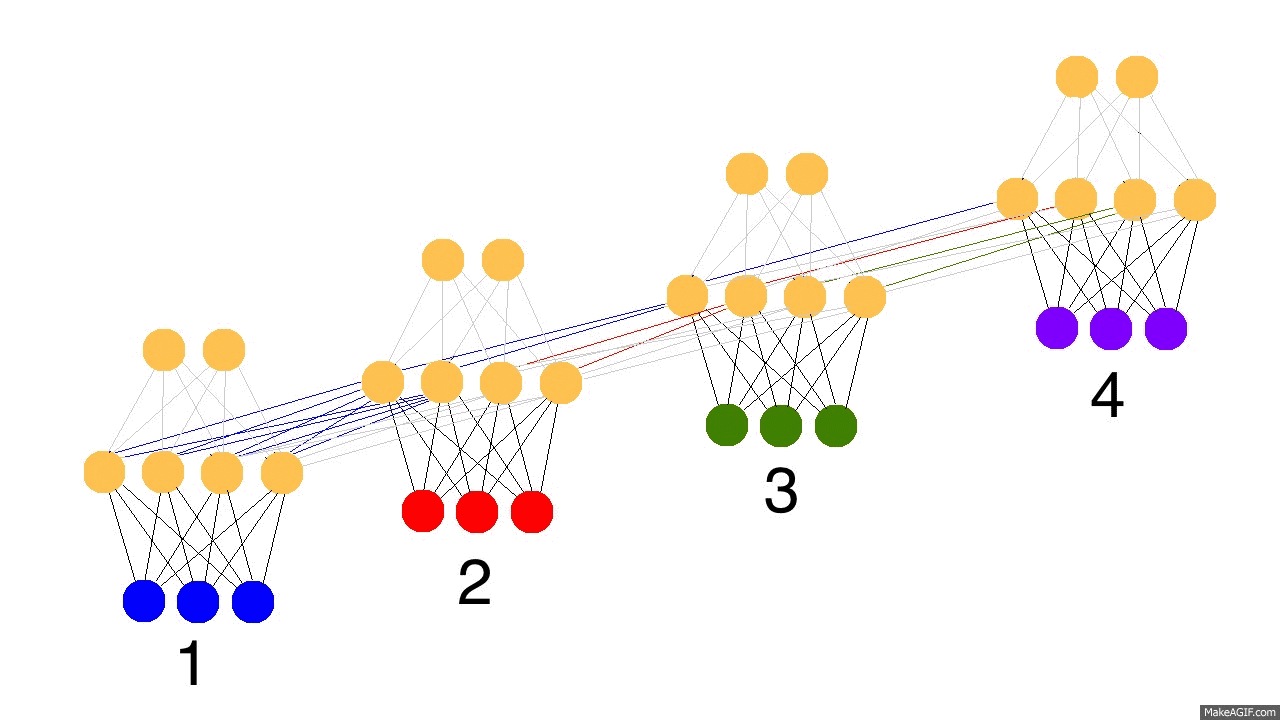
很多时候大家看到的 RNN 网络结构都很迷糊。有上面那个图样子的,还有这样的:
还有的是这样的:
实际上第一个图把递归过程画到图里面了,这样就把图画的过于复杂;上面这个图把递归过程按序列的时间顺序(timestep)展开了,也就是 unfold 的表达,但是由于无法跟网络结构对应起来,看起来不够清晰。
引用 wikipedia 上面一个图,这个图把输入(以文本序列为例,就是一个个的词)用 a 表示(下文用 x 表示),隐藏层的输出用 x 表示(下文用 b 表示),最后输出用 y 表示。t 表示的是时间关系,还是以文本为例,t+1 就是 t 的下一个词,但是这个图中 f 也带了下标,不容易看明白。
结合上面三个图,各理解一部分最后综合就好理解了。
RNN 的网络结构上跟 DNN 类似(第一个图去掉 hidden unit 之间的那些连接),但是每个 timestep hidden unit 的输入分两部分(第三个图):一部分是前一层的输出作为本层 unit 的输入,另外一部分是相同 hidden layer 所有的 unit 在上一个 timestep 的输出,这两部分通过不同的权重加权求和,一起作为本时刻的输入。
另外需要理解的是,RNN 并没用若干个 model 用于处理不同的 timestep 数据,而是只有一个 model ,第二个图中一个黑圈代表一个 hidden layer ,不同层的权重 Wi 在所有 timestep 使用的是一份相同的参数,这也就是从 time 1 到5 ,input to hidden 一直是 W1,hidden to hidden 一直是 W2,hidden to output 一直是 W3 。
这里贴一个动画图来辅助理解RNN,不同timestep共用一个NN模型,上一时刻hidden layer的输出,与下一时刻的输入合并作为新的输入。图上面还演示了反馈的过程,这个后面再详细讲述。
RNN 的前馈过程与普通的神经网络是一样的,但是有一点需要注意:隐藏层节点的输入,除了有普通的数据输入部分,还有上一时刻(timestep)隐藏层的输出部分。假设输入序列 X 长度为 T(还是以一个句子举例,有 T 个词),输入到一个 RNN 网络中,输入层是 I 个输入单元(也可以直观理解为 word embedding 到 I 维),H 个隐藏单元,K 个输出单元(最后softmax对应的label是K种)。设 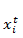
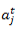
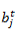
也就是说,任意时刻 t ,隐藏层节点的输入包含原始数据输入和上一时刻隐藏层输出两部分。注意:编程实现的时候,这部分是做矩阵元素的按位求和操作。我们把节点输出的激活函数部分单独分离出来,有如下关系:
计算过程中,比如对一句话进行 RNN 分类,从 t=1 开始到 t=T 结束(一个词一个词的往网络中输入),递归的调用上面的两个公式,得到隐藏层输出。在最后的输出层,由于他不需要递归调用,因此只需要对隐藏层的输出进行全连接加权求和,最后应用 softmax 或者 logistic 激活函数即可:
这里有个疑问:每次输入一个词,理论上都可以前向计算到最后的输出层,得到一个输出层的输出,如果是分类问题,要怎么处理这么多的输出呢?有三种解决办法:
a) 把每个时刻输出结果都存下来,最后合并做一次 pooling ,然后对 pooling 结果做最后到分类 label 的映射;
b) 把每个时刻输出结果都存下来,但是是合并到一个向量上,统一通过输出层做最后到分类 label 的映射;
c) t=1 到 t=T-1 时刻最后隐藏层的输出都只做下一个 timestep 的输入,而不连接到 output layer ,只保留 t=T 时刻的输出,做到分类 label 的映射。
上述三种方法,经过试验都是可以 work 的,但是由于他们对最后的误差 backward 是有区别的,所以收敛速度和效果也都不一样,大家可以自己试验一下。
另外一个问题是:在起始时刻(输入第一个词的时候),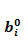
与普通神经网络一样,通过对输出层目标函数的偏导,传递回来对隐藏层网络的权重求导数。目前有两种方案对 RNN 网络的参数进行求导,一种是 real time recurrent learning(RTRL),一种是 backpropagation through time(BPTT)。下面主要介绍 BPTT 算法,因为他比较简单,而且更加高效。
与标准 BP 算法一样,BPTT 也是从最后一层向前面传播。微妙之处是,对于 RNN 的目标函数虽然依赖于隐藏层的激活输出,但是隐藏层的激活输出不但会影响到输出层,而且还会影响下一时刻的隐藏层自身。比如:
其中: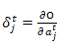
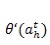
要计算一个序列的 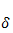
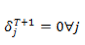
最后,需要注意的是:用于连接隐藏层节点的输入输出的参数(各种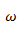
对于很多序列标注问题,我们是使用前面的已知内容去预测后面的内容。但是仍然有另外一些序列标注问题,上下文都是已知的。文本分类问题就是最典型的此类问题。
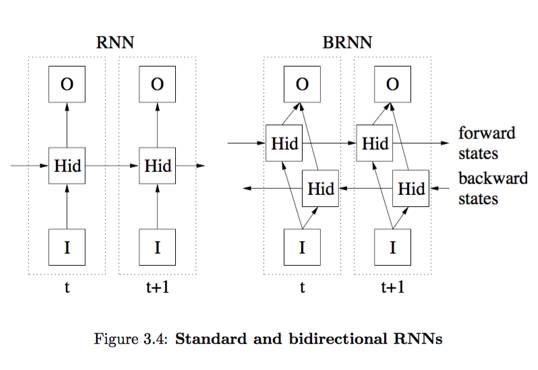
显然序列数据的前后元素之间都是有关联的,RNN 描述的就是沿着时间轴方向的关联性。所以理论上我们可以反过来,沿着逆时间轴的顺序对序列数据进一步刻画。这就是双向 RNN 。
具体内容这里就不展开了,留给自己调研学习吧。



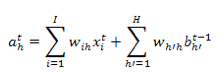
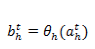
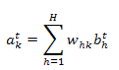
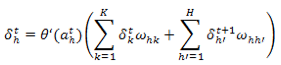
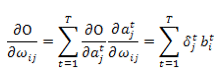

 微信ID:WeChatAI
微信ID:WeChatAI
 长按左侧二维码关注
长按左侧二维码关注