Equivalence testing for standardized effect sizes in linear regression

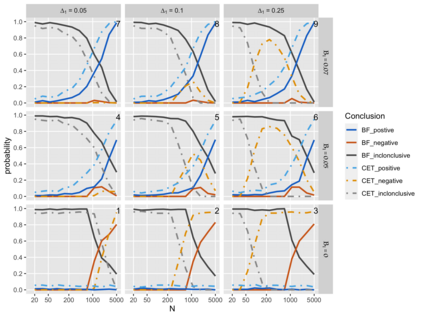
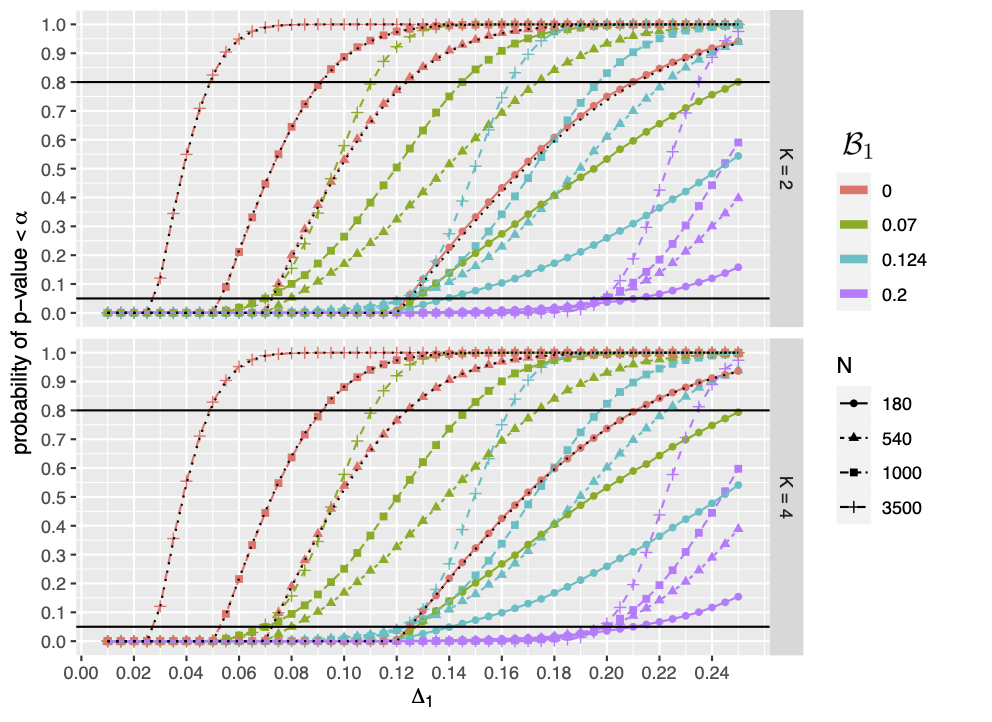
In this paper, we introduce equivalence testing procedures for standardized effect sizes in a linear regression. We show how to define valid hypotheses and calculate p-values for these tests. Such tests are necessary to confirm the lack of a meaningful association between an outcome and predictors. A simulation study is conducted to examine type I error rates and statistical power. We also compare using equivalence testing as part of a frequentist testing scheme with an alternative Bayesian testing approach. The results indicate that the proposed equivalence test is a potentially useful tool for "testing the null."