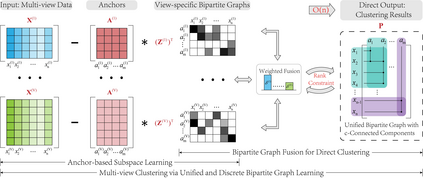
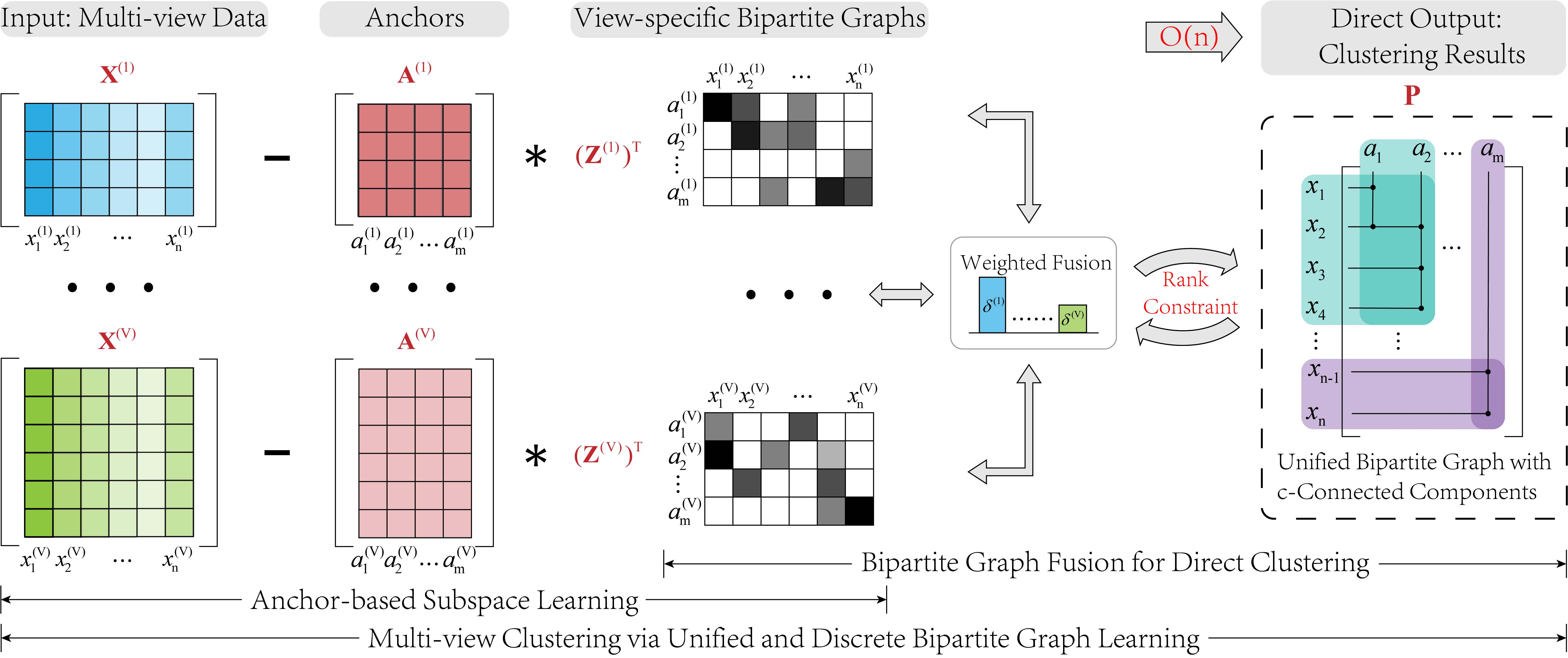
Although previous graph-based multi-view clustering algorithms have gained significant progress, most of them are still faced with three limitations. First, they often suffer from high computational complexity, which restricts their applications in large-scale scenarios. Second, they usually perform graph learning either at the single-view level or at the view-consensus level, but often neglect the possibility of the joint learning of single-view and consensus graphs. Third, many of them rely on the $k$-means for discretization of the spectral embeddings, which lack the ability to directly learn the graph with discrete cluster structure. In light of this, this paper presents an efficient multi-view clustering approach via unified and discrete bipartite graph learning (UDBGL). Specifically, the anchor-based subspace learning is incorporated to learn the view-specific bipartite graphs from multiple views, upon which the bipartite graph fusion is leveraged to learn a view-consensus bipartite graph with adaptive weight learning. Further, the Laplacian rank constraint is imposed to ensure that the fused bipartite graph has discrete cluster structures (with a specific number of connected components). By simultaneously formulating the view-specific bipartite graph learning, the view-consensus bipartite graph learning, and the discrete cluster structure learning into a unified objective function, an efficient minimization algorithm is then designed to tackle this optimization problem and directly achieve a discrete clustering solution without requiring additional partitioning, which notably has linear time complexity in data size. Experiments on a variety of multi-view datasets demonstrate the robustness and efficiency of our UDBGL approach.
翻译:虽然先前基于图形的多视图群集算法取得了显著进展,但其中多数仍面临三个限制。 首先,它们往往受到高计算复杂性的制约,这限制了其在大型情景下的应用。 其次,它们通常在单一视图级别或视图-共识级别上进行图形学习,但往往忽视联合学习单一视图和共识图形的可能性。 第三,它们中的许多依赖以美元为单位的分解光谱嵌入图,它们缺乏直接学习离散集群结构的图表的能力。 有鉴于此,本文件通过统一和离散双部分图学习(UDBGL),展示了高效多视角组合法的高效多视角组合法。 具体地说,基于锁定的子空间学习是为了从多种观点中学习针对具体视图的双部分图表和共识图。 双面图的组合组合法制约是确保双部分的组合图集具有离散的多视角, 并且通过双向的直径直流数据流数据流化结构,同时展示了该双向的双向组合和双向的组合式数据学习。