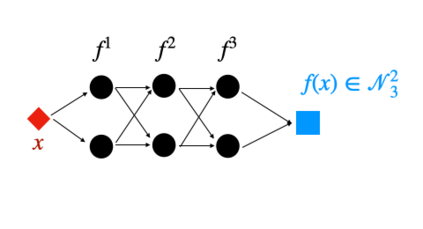
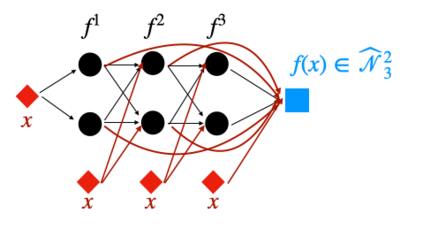
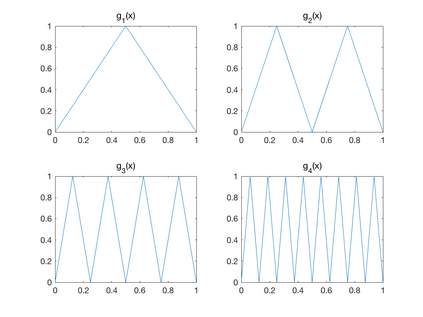
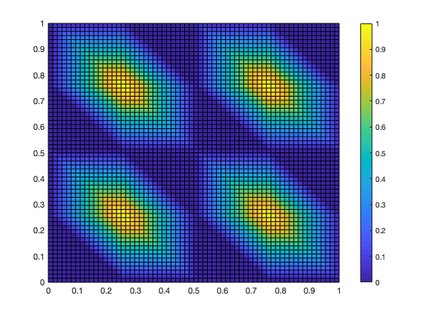
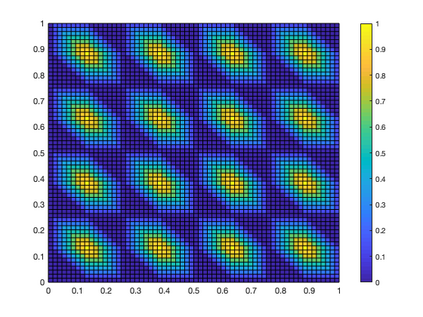
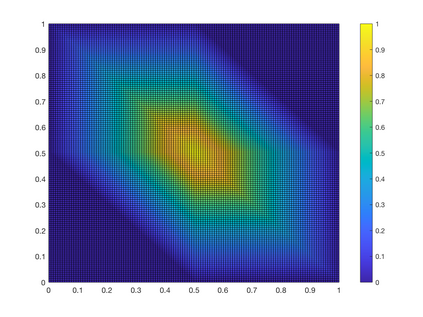
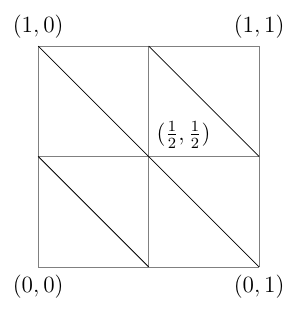
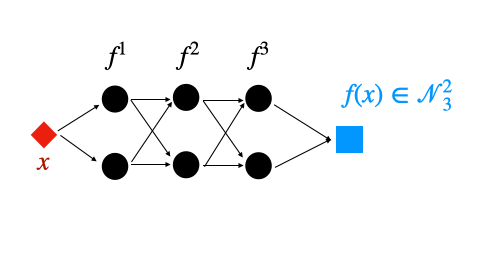
We study ReLU deep neural networks (DNNs) by investigating their connections with the hierarchical basis method in finite element methods. First, we show that the approximation schemes of ReLU DNNs for $x^2$ and $xy$ are composition versions of the hierarchical basis approximation for these two functions. Based on this fact, we obtain a geometric interpretation and systematic proof for the approximation result of ReLU DNNs for polynomials, which plays an important role in a series of recent exponential approximation results of ReLU DNNs. Through our investigation of connections between ReLU DNNs and the hierarchical basis approximation for $x^2$ and $xy$, we show that ReLU DNNs with this special structure can be applied only to approximate quadratic functions. Furthermore, we obtain a concise representation to explicitly reproduce any linear finite element function on a two-dimensional uniform mesh by using ReLU DNNs with only two hidden layers.
翻译:我们研究RELU深神经网络(DNNs),方法是调查这些网络与有限元素方法中的等级基法的联系。首先,我们表明,RELU DNS的近似方案是这两个功能的等级基近似的构成版本。根据这一事实,我们获得一个几何解释和系统证据,以证明多边元素的RELU DNNs的近似结果,它在RELU DNS的一系列近期指数近似结果中发挥了重要作用。通过调查RELU DNS与等级基近似之间的连接,我们显示,使用这一特殊结构的RELU DNS只能用于大约的四边函数。此外,我们获得一个简明的表述,通过使用只有两个隐藏层的RELU DNS来明确复制二维统一网格的任何线性定要素函数。