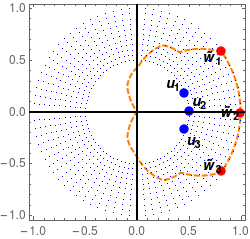
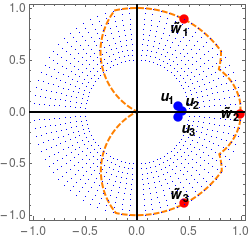
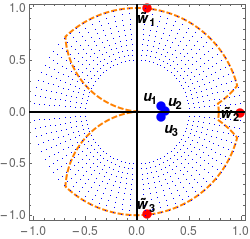
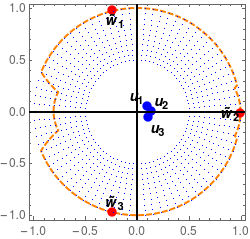
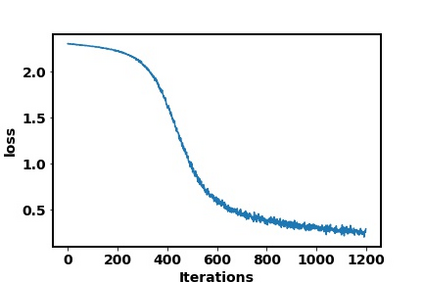
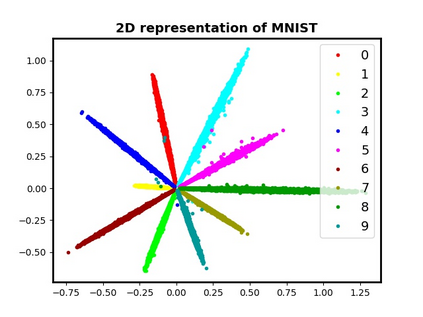
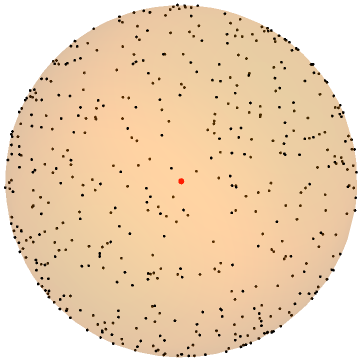
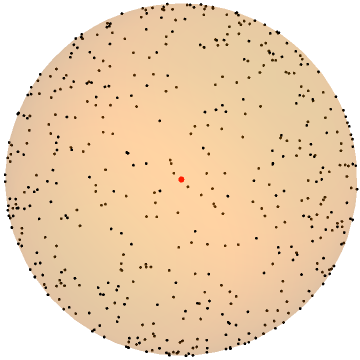
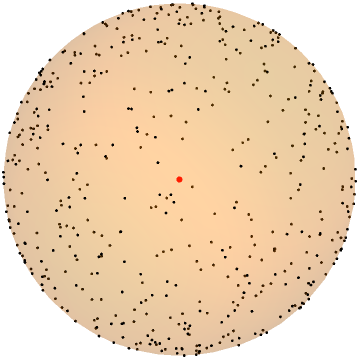
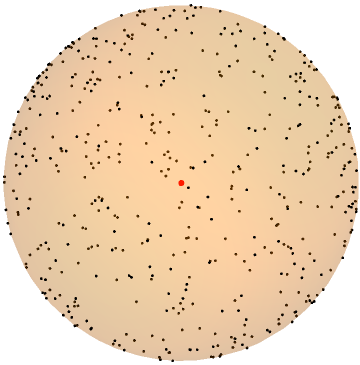
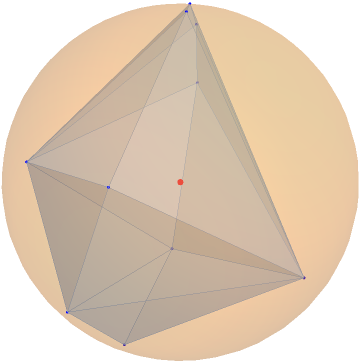
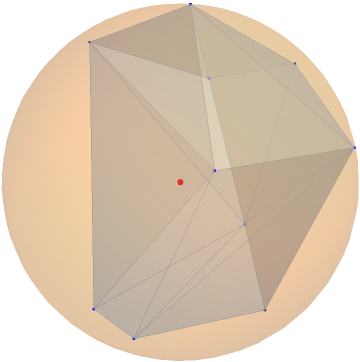
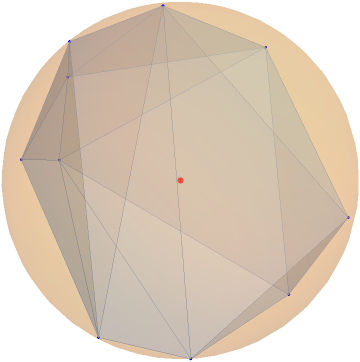
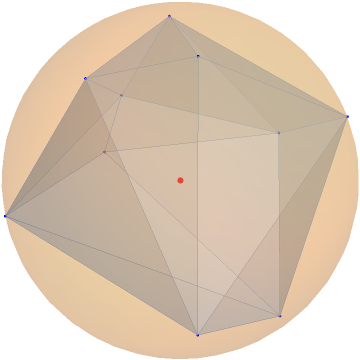
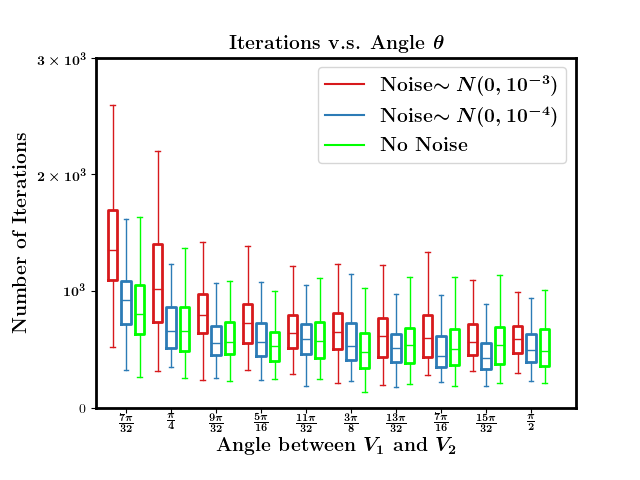
In this paper, we study the dynamics of gradient descent in learning neural networks for classification problems. Unlike in existing works, we consider the linearly non-separable case where the training data of different classes lie in orthogonal subspaces. We show that when the network has sufficient (but not exceedingly large) number of neurons, (1) the corresponding minimization problem has a desirable landscape where all critical points are global minima with perfect classification; (2) gradient descent is guaranteed to converge to the global minima. Moreover, we discovered a geometric condition on the network weights so that when it is satisfied, the weight evolution transitions from a slow phase of weight direction spreading to a fast phase of weight convergence. The geometric condition says that the convex hull of the weights projected on the unit sphere contains the origin.
翻译:在本文中,我们研究了学习神经网络中的梯度下降动态,以研究分类问题。与现有工作不同,我们考虑了不同类别培训数据处于正正方位子空间的线性不可分离案例。我们表明,当网络拥有足够(但并不大)数量的神经元时,(1) 相应的最小化问题具有理想的景观,其中所有临界点都是全球微型,分类完美;(2) 梯度下降保证与全球微型相一致。此外,我们发现网络重量存在几何条件,因此当满足时,重量变化从一个缓慢的重量方向向向向向向向向向向向向向向向向向向向向向向向向向,向一个快速的重量趋同阶段发展。几何条件显示,在单位领域预测的重量的螺旋体壳包含着重量的起源。