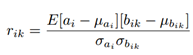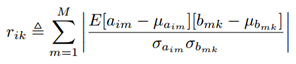Sparsifying Neural Network Connections for Face Recognition

摘要

论文提出了一种对网络中的神经元连接进行稀疏的方法，最终得到的稀疏后的网络称为sparse ConvNets。实验表明直接从头开始学习一个稀疏卷积网络往往得不到令人满意的结果，因此本文通过迭代的方式来学习稀疏卷积网络。首先训练一个传统的密集型网络，然后从后向前逐层的进行稀疏化，直至第一层也被稀疏完成。最终的实验表明，只需要原始网络12%的参数就可以达到和原始网络相同的性能；而采取适当的稀疏结构时(原始网络参数的26%-76%)，学习到的稀疏卷积网络与之前的模型相比性能得到了很大的提升。下面详细的介绍一下本文提出的方法。

基本思想

本文的基本思想很简单，通过两个神经元之间的相关性程度来决定是否保留它们之间的连接。如果当前层的一个神经元a和前一层的神经元b相关性比较强，说明神经元b对于神经元a具有很强的预测能力，则应该保留它们之间的连接；而如果a和b的相关性较弱，则说明前一层的神经元b与它后一层的神经元a关系不大，不会对a产生很大的影响，于是将它们之间的连接删去。但是实验表明保留少量的相关性较弱的连接对于提高网络的性能也是有好处的，这可能是因为这些弱相关性的连接提供了一些补充信息。

算法流程

算法的大体流程如下：

(1)训练一个原始的密集型网络。

(2)从最后一层开始到第一层为止，逐层迭代对网络进行稀疏。其中稀疏性准则为:计算当前层中每个神经元a_i与前一层中与a_i相连接的所有神经元的相关性，根据相关性强弱来决定是否保留这个连接。具体的保留策略和神经元之间相关性计算的方法会在随后介绍。值得注意的是，每一层在稀疏完成后，重新训练网络，得到的网络模型用于在下一次稀疏中计算相关性。

相关细节

(1)原始的密集型网络

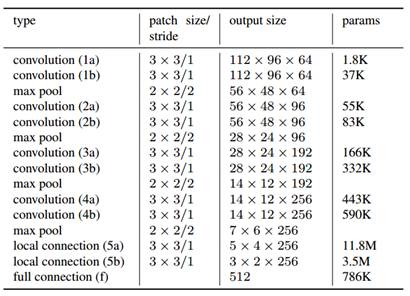
文中使用的是一个类似于VGG net的卷积神经网络，每两个卷积层后面跟一个最大池化层，最后是一个全连接层。它和VGGnet最大的不同之处在于将VGG net中的最后两层卷积层换成了局部连接层(本篇论文是用于人脸识别的，因此加入局部连接层来利用人脸的结构化特点)。网络的结构如下：

激活函数是ReLU函数，局部连接层和全连接层的dropout率分别是30%和50%。

(2)神经元之间的相关性计算

局部连接层和全连接层的权值不共享，计算规则比较简单，而卷积层的权值共享，计算起来较为复杂。它们的计算相关性的规则有所不同。

(i)局部连接层和全连接层

对于当前层的一个神经元a_i，前一层和它相连的K个神经元记为b_ik（k=1,2,…,K），则a_i和b_ik的相关性系数为：

其中均值和方差都是由一个单独的训练数据集计算得到的。

(ii)卷积层

记a_im为当前层中第i个feature map中的第m个神经元(m=1,2,…,M.其中M表示卷积后得到的feature map的大小), 上一层中和它相连接的所有神经元记为b_mk(k=1,2,…,K.其中K是滤波器的大小)。则a_im和b_mk的相关性系数为：

(3)神经元连接的保留策略

前面提到，我们倾向于保留相关性比较强的神经元之间的连接，同时还要有少量的相关性较弱的神经元之间连接。需要注意的是，负相关和正相关的地位是一样的，同等看待，负相关也同等重要。

在计算出神经元之间的相关性系数之后，将正相关与负相关分开处理，这里以正相关为例说明本文的策略。将所有的正相关系数降序排列，然后从中间均匀分为两部分，正相关的数量记为K⁺。然后在前半部分随机采样λSK⁺个，后半部分随机采样(1-λ) SK⁺个，其中S表示稀疏程度，λ控制选取的强相关与弱相关的比例，文中设置λ为0.75，也就是75%的连接是强相关的，25%是弱相关的。同理，负相关也是如此。这些被采样到的相关系数对应的神经元之间的连接被保留，其余的则被删去。

实验

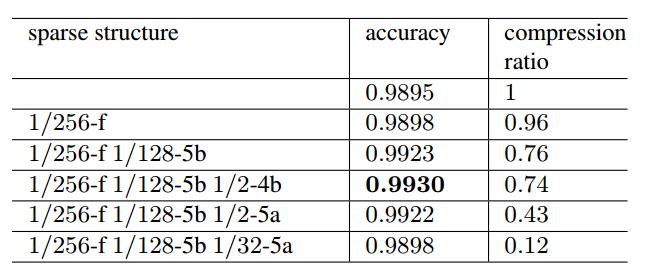
实验结果如下

本文做了多组实验，详细的实验内容可通过点击下面的阅读原文来阅读原论文。