On Regularization via Frame Decompositions with Applications in Tomography

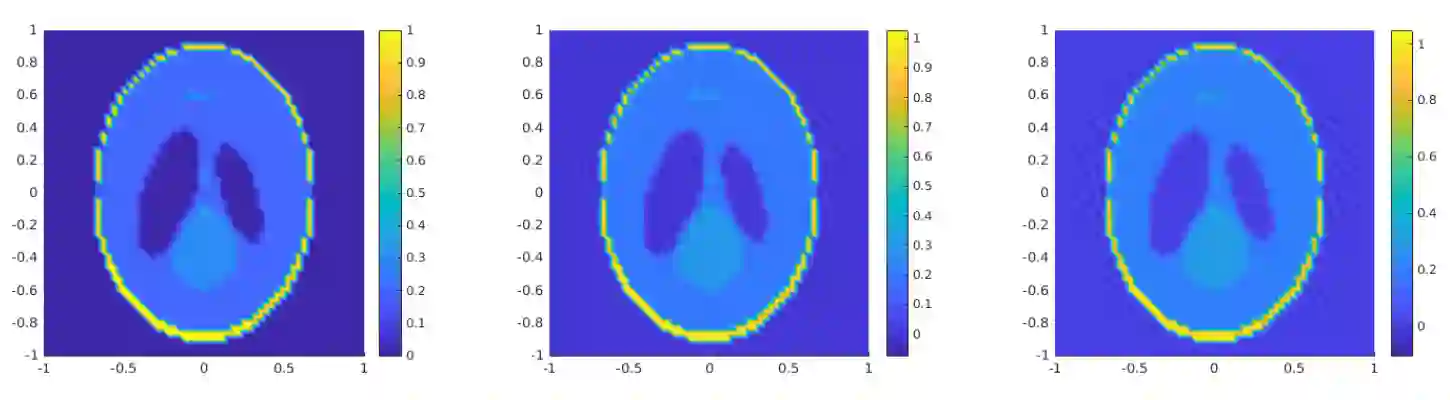
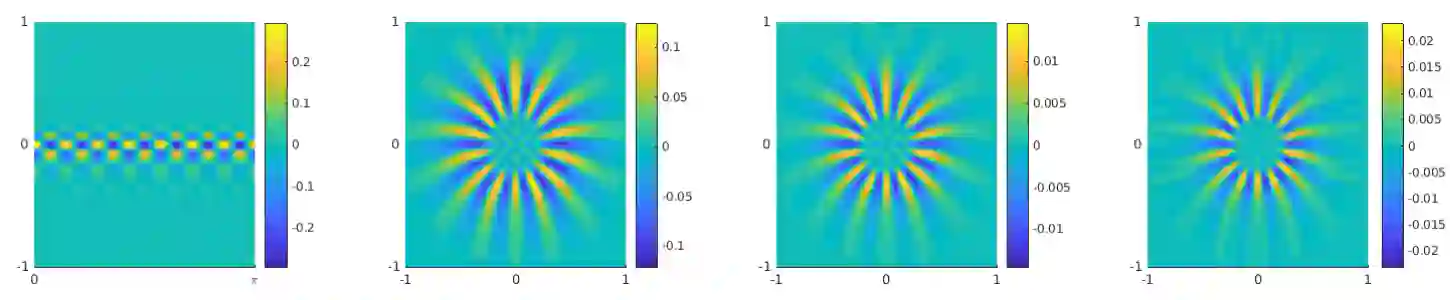
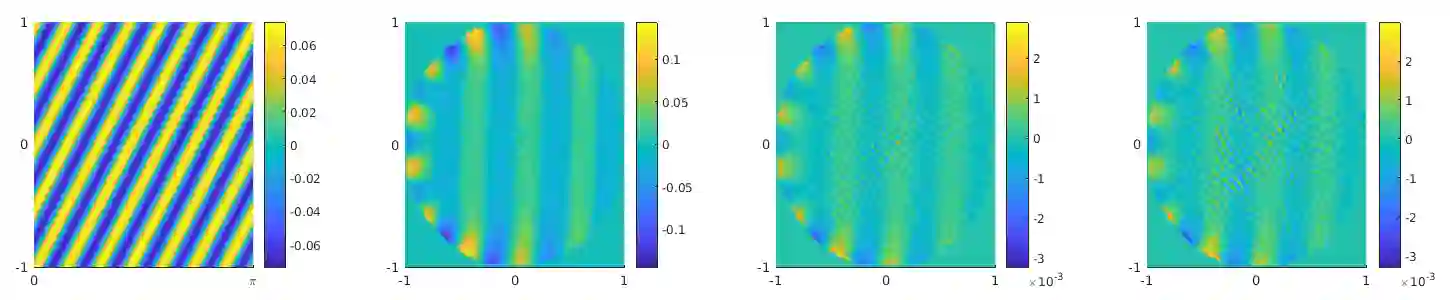
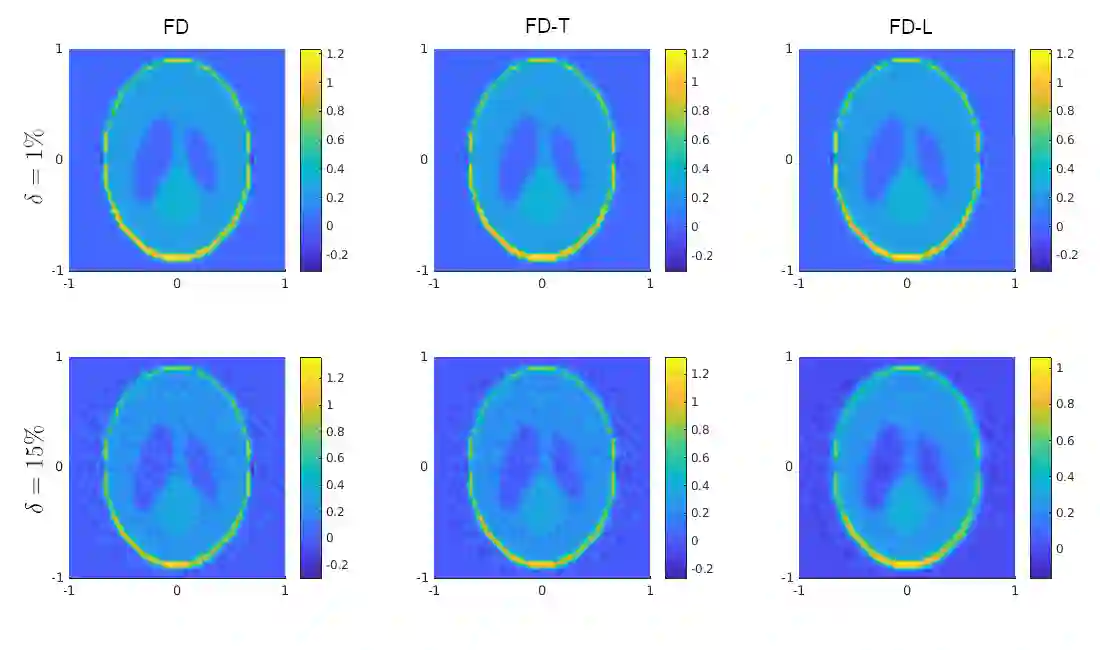
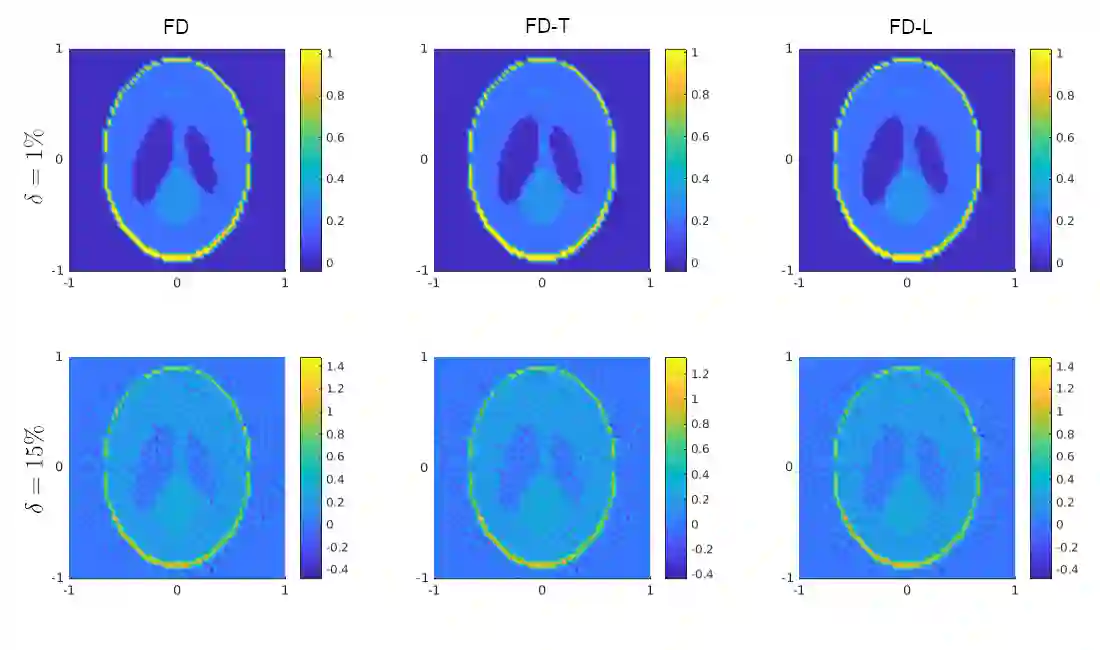
In this paper, we consider linear ill-posed problems in Hilbert spaces and their regularization via frame decompositions, which are generalizations of the singular-value decomposition. In particular, we prove convergence for a general class of continuous regularization methods and derive convergence rates under both a-priori and a-posteriori parameter choice rules. Furthermore, we apply our derived results to a standard tomography problem based on the Radon transform.