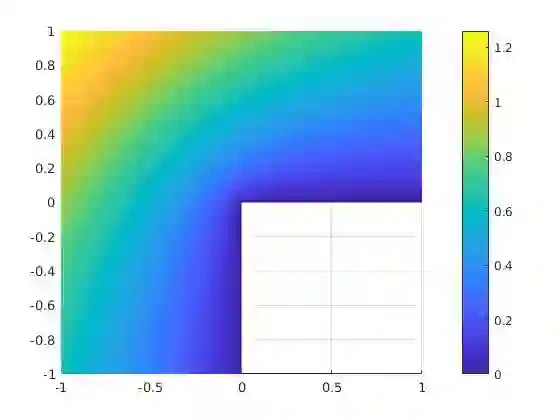
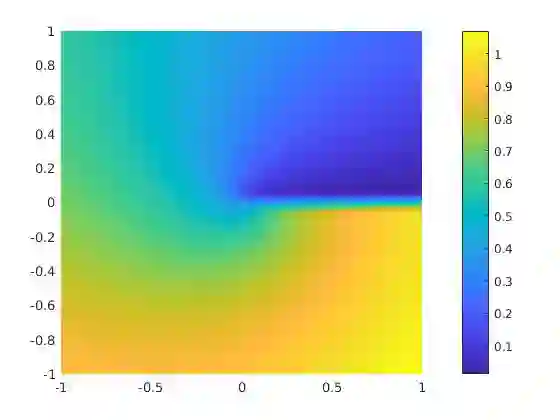
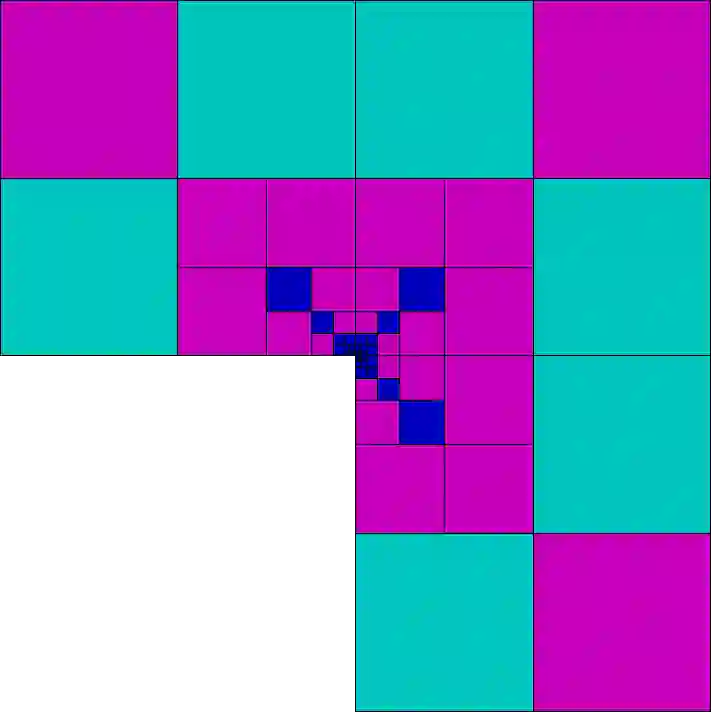
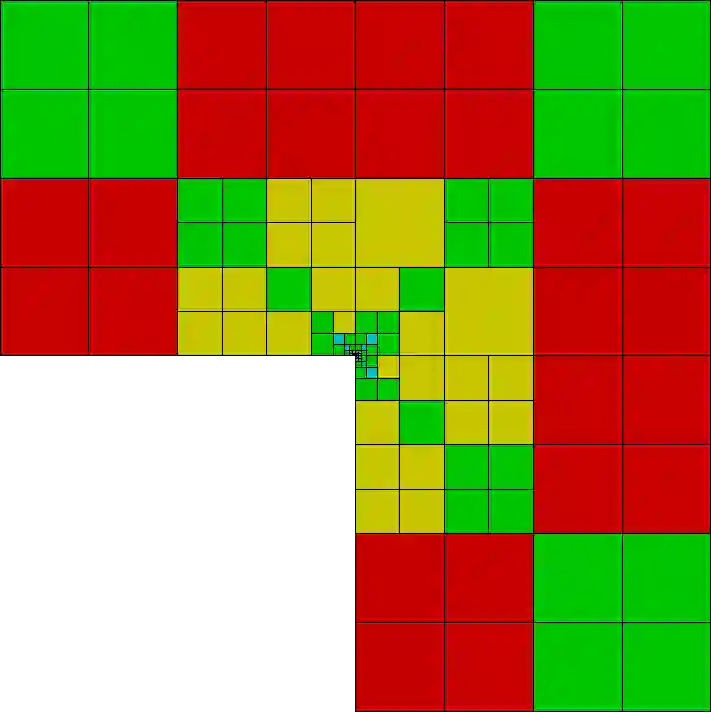
We present an hp-adaptive virtual element method (VEM) based on the hypercircle method of Prager and Synge for the approximation of solutions to diffusion problems. We introduce a reliable and efficient a posteriori error estimator, which is computed by solving an auxiliary global mixed problem. We show that the mixed VEM satisfies a discrete inf-sup condition, with inf-sup constant independent of the discretization parameters. Furthermore, we construct a stabilization for the mixed VEM, with explicit bounds in terms of the local degree of accuracy of the method. The theoretical results are supported by several numerical experiments, including a comparison with the residual a posteriori error estimator. The numerics exhibit the p-robustness of the proposed error estimator. In addition, we provide a first step towards the localized flux reconstruction in the virtual element framework, which leads to an additional reliable a posteriori error estimator that is computed by solving local (cheap-to-solve and parallelizable) mixed problems. We provide theoretical and numerical evidence that the proposed local error estimator suffers from a lack of efficiency.
翻译:我们根据Prager 和 Synge 的超圆轴法提出了一种 hp-适应性虚拟元件方法(VEM), 以近似扩散问题的解决办法。 我们引入了可靠而高效的事后误差估计器, 其计算方法是解决一个辅助性的全球混合问题。 我们显示混合的 VEM 满足一个离散的内向性条件, 与离散参数无关的内向性常数常数 。 此外, 我们为混合的 VEM 构建了一个稳定度, 其精确度以当地方法的准确度为明确界限 。 理论结果得到了数项实验的支持, 包括与残余的后向误差估计器的比较。 数字显示了拟议误差估计器的p- robust 。 此外, 我们为虚拟要素框架中的局部通量性通量重建提供了第一步, 导致额外的可靠的后向误估计器, 通过解决本地( 草到溶和平行) 混合问题来计算。 我们提供了理论和数字证据, 证明拟议的局部误差估计器缺乏效率。