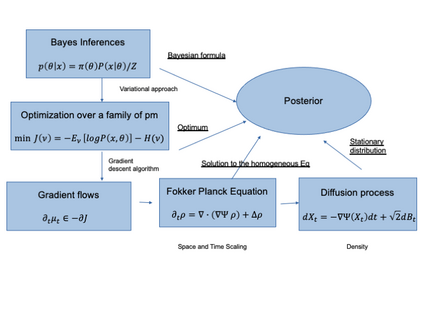
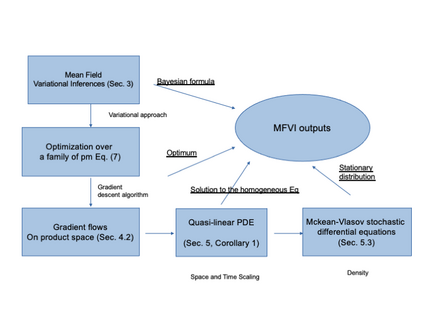
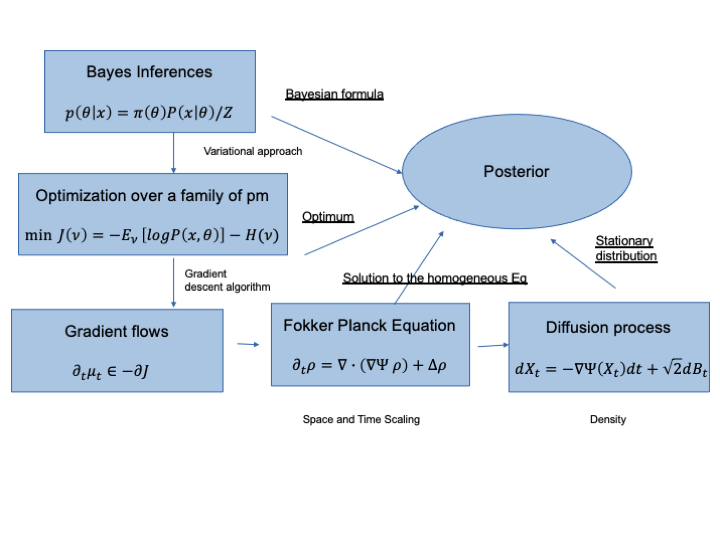
The mean field variational inference (MFVI) formulation restricts the general Bayesian inference problem to the subspace of product measures. We present a framework to analyze MFVI algorithms, which is inspired by a similar development for general variational Bayesian formulations. Our approach enables the MFVI problem to be represented in three different manners: a gradient flow on Wasserstein space, a system of Fokker-Planck-like equations and a diffusion process. Rigorous guarantees are established to show that a time-discretized implementation of the coordinate ascent variational inference algorithm in the product Wasserstein space of measures yields a gradient flow in the limit. A similar result is obtained for their associated densities, with the limit being given by a quasi-linear partial differential equation. A popular class of practical algorithms falls in this framework, which provides tools to establish convergence. We hope this framework could be used to guarantee convergence of algorithms in a variety of approaches, old and new, to solve variational inference problems.
翻译:平均场变差推断(MFVI)的配方限制了Bayesian一般推论问题与产品计量的子空间的亚空间。我们提出了一个分析MFVI算法的框架,这个框架的灵感来自对通用变差Bayesian配方的类似发展。我们的方法使MFVI问题以三种不同的方式得到体现:瓦塞斯坦空间的梯度流、Fokker-Planck式方程式的系统以及扩散过程。建立了严格的保证,以表明在产品瓦塞斯坦测量空间的坐标变差算法中以时间分解的方式执行协调变差算法在极限中产生梯度流。一个类似的结果是其相关的密度,其限制由准线性部分差异方程式提供。一个流行的实用算法属于这个框架,它提供了实现趋同的工具。我们希望这个框架可以用来保证在各种新旧方法中使算法趋于一致,以解决变异性问题。