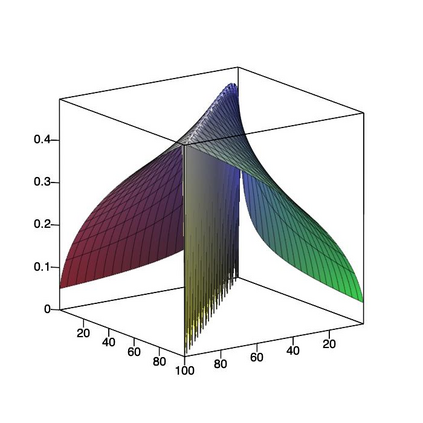
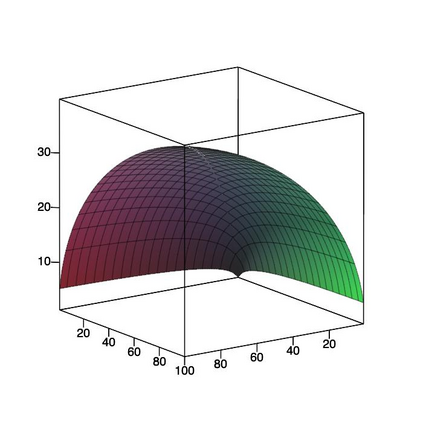
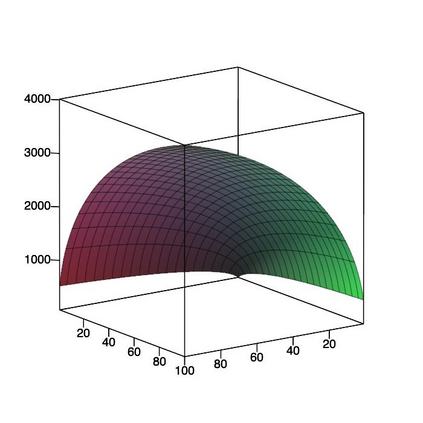
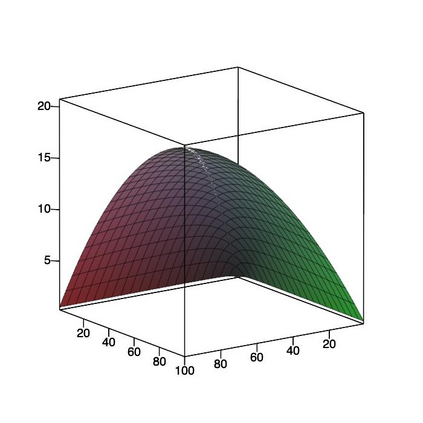
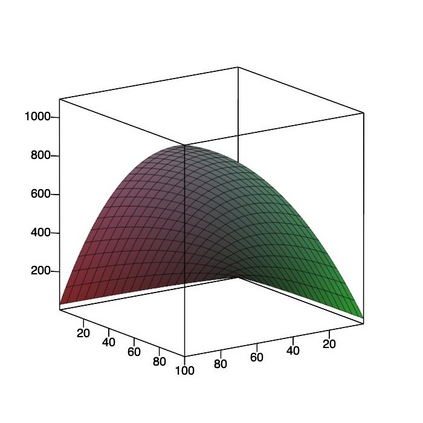
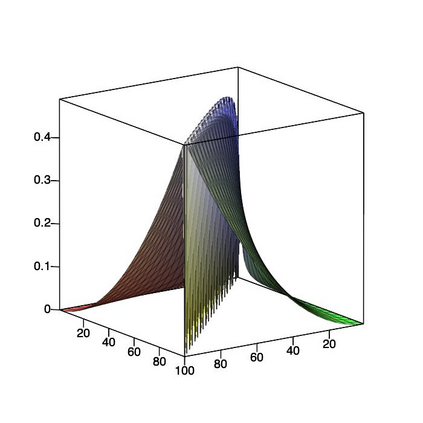
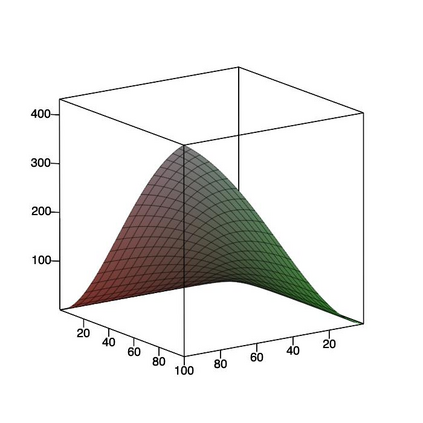
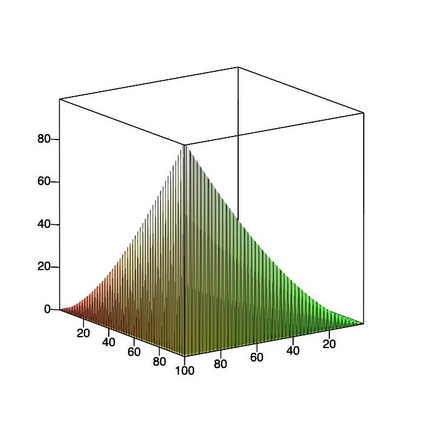
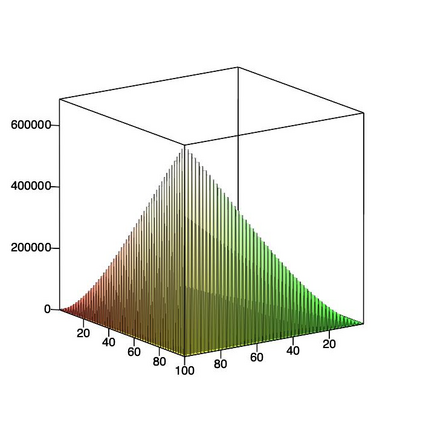
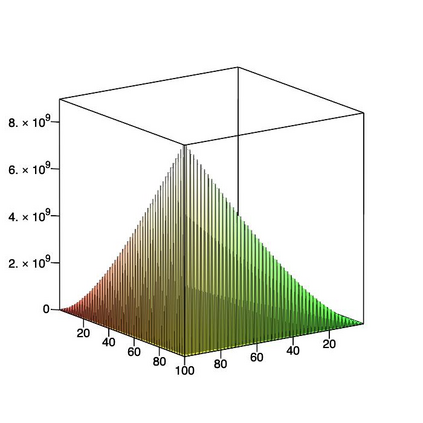
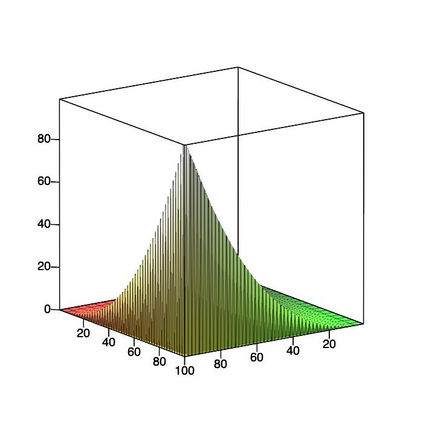
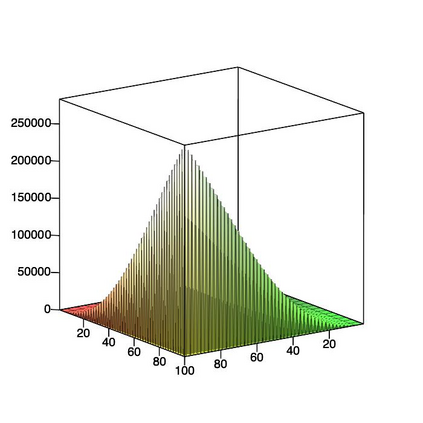
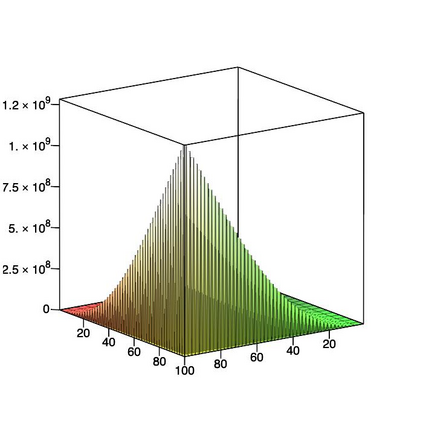
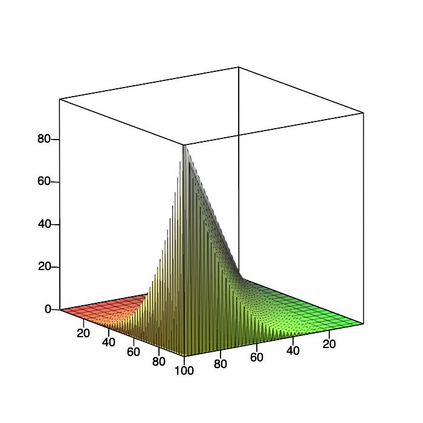
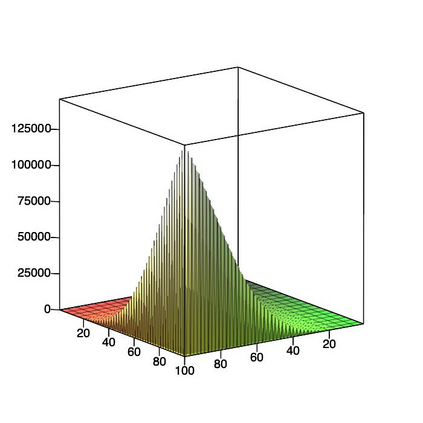
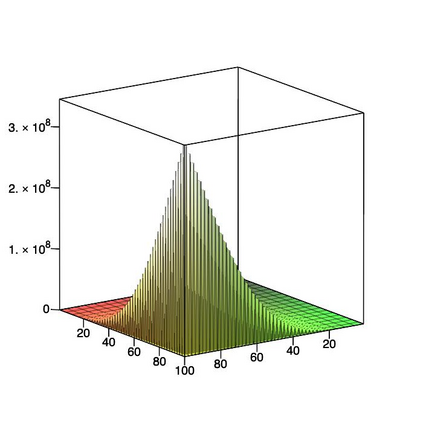
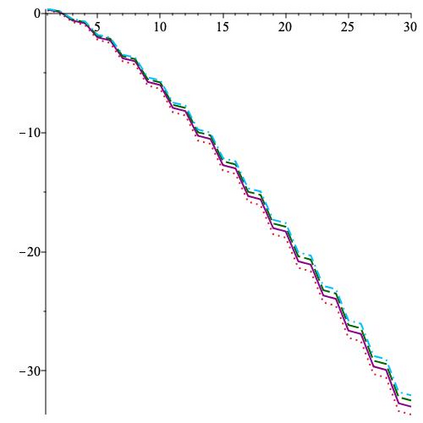
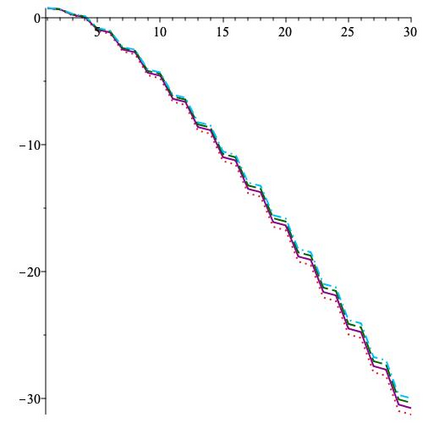
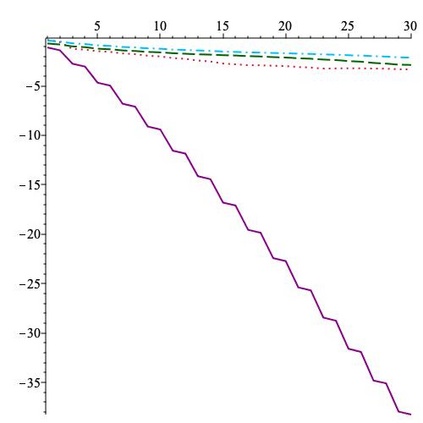
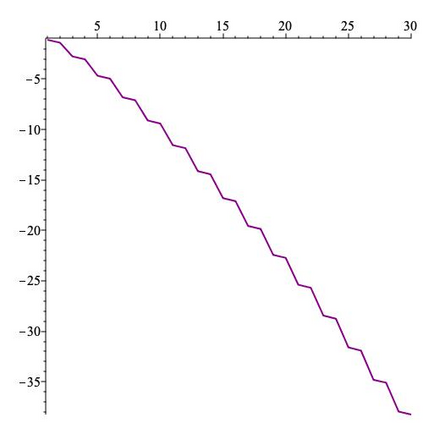
This paper is concerned with orthonormal systems in real intervals, given with zero Dirichlet boundary conditions. More specifically, our interest is in systems with a skew-symmetric differentiation matrix (this excludes orthonormal polynomials). We consider a simple construction of such systems and pursue its ramifications. In general, given any $\mathrm{C}^1(a,b)$ weight function such that $w(a)=w(b)=0$, we can generate an orthonormal system with a skew-symmetric differentiation matrix. Except for the case $a=-\infty$, $b=+\infty$, only a limited number of powers of that matrix is bounded and we establish a connection between properties of the weight function and boundedness. In particular, we examine in detail two weight functions: the Laguerre weight function $x^\alpha \mathrm{e}^{-x}$ for $x>0$ and $\alpha>0$ and the ultraspherical weight function $(1-x^2)^\alpha$, $x\in(-1,1)$, $\alpha>0$, and establish their properties. Both weights share a most welcome feature of {\em separability,\/} which allows for fast computation. The quality of approximation is highly sensitive to the choice of $\alpha$ and we discuss how to choose optimally this parameter, depending on the number of zero boundary conditions.
翻译:本文关注的是真实间隔的正方形系统, 以零 Dirichlet 边界条件为条件 。 更具体地说, 我们感兴趣的是具有 skiw- infty 差异矩阵的系统( 不包括正反偏差多式模型 ) 。 我们考虑的是这种系统的简单构造, 并追求其影响 。 一般来说, 任何美元( a) = w ( b) = w ( b) = 0 美元, 我们就可以以敏感度对称差异矩阵生成一个正方形系统 。 除了案件 $=-\ infty 差异矩阵的系统( 不包括正反正反偏差组合 ) 。 我们考虑的是这种系统简单构建的重函数属性和约束性 。 特别是, 我们仔细检查了两个重量函数: Laguerre 重量函数 $x alphain { { { { eg-x} 美元, 我们可以以 $\ x $ 来选择一个敏感度的正对称矩阵值 $ ( $_xx2) 比例 。