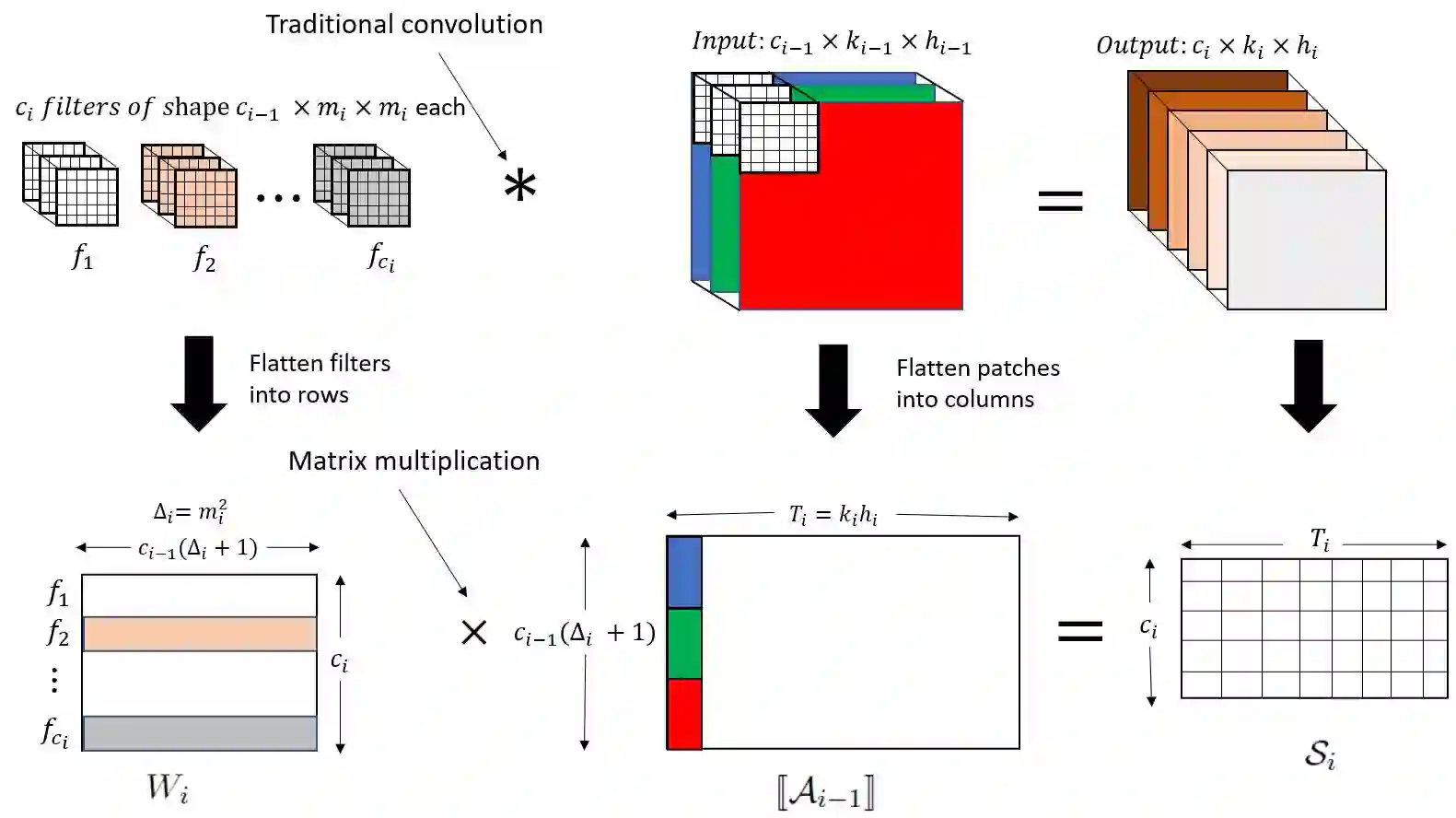
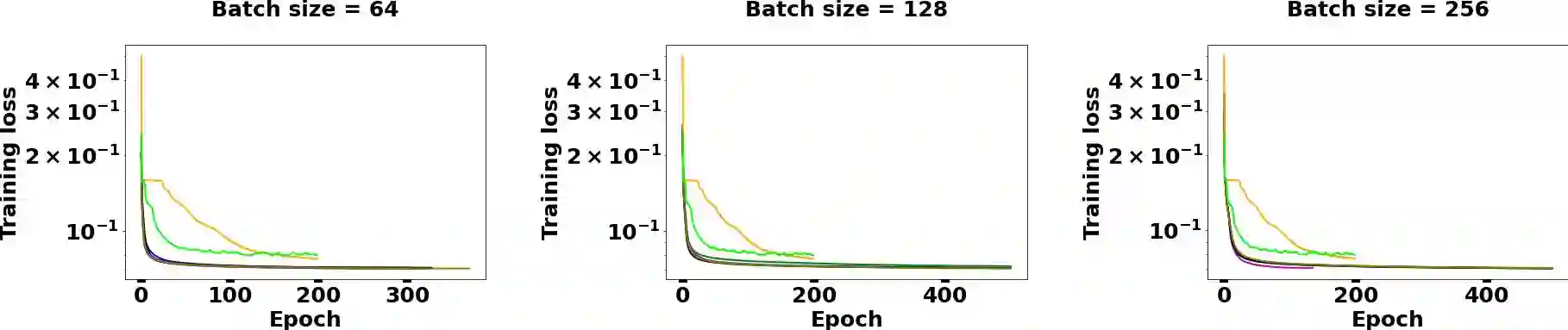
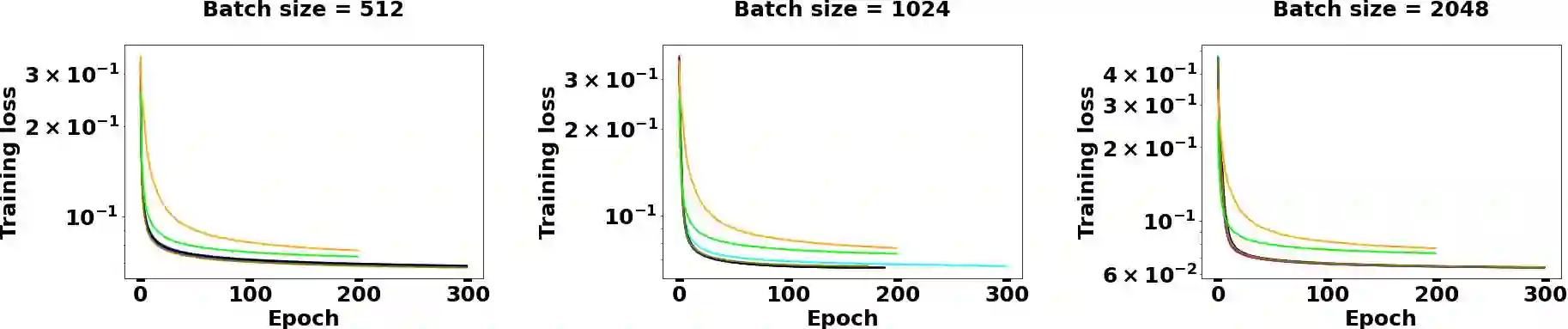
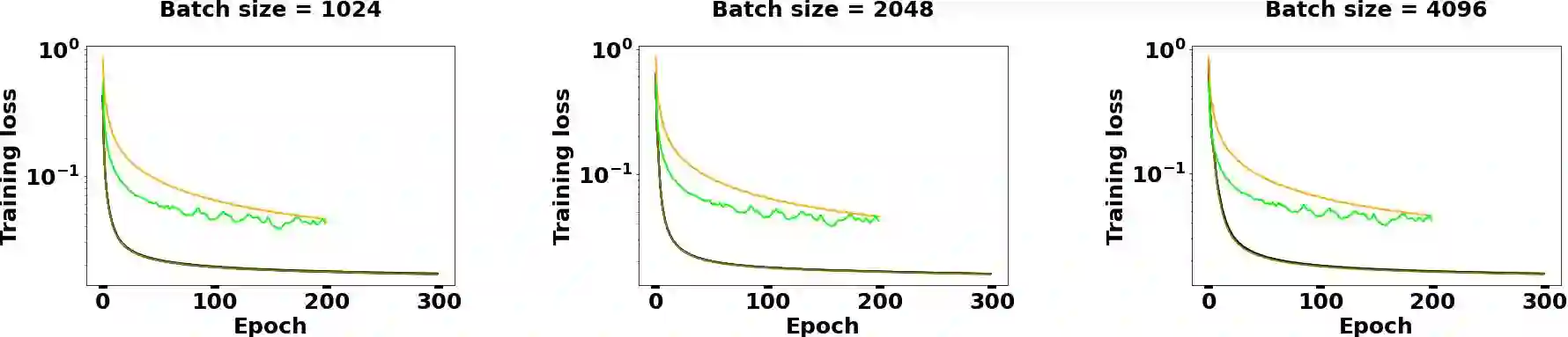
As a second-order method, the Natural Gradient Descent (NGD) has the ability to accelerate training of neural networks. However, due to the prohibitive computational and memory costs of computing and inverting the Fisher Information Matrix (FIM), efficient approximations are necessary to make NGD scalable to Deep Neural Networks (DNNs). Many such approximations have been attempted. The most sophisticated of these is KFAC, which approximates the FIM as a block-diagonal matrix, where each block corresponds to a layer of the neural network. By doing so, KFAC ignores the interactions between different layers. In this work, we investigate the interest of restoring some low-frequency interactions between the layers by means of two-level methods. Inspired from domain decomposition, several two-level corrections to KFAC using different coarse spaces are proposed and assessed. The obtained results show that incorporating the layer interactions in this fashion does not really improve the performance of KFAC. This suggests that it is safe to discard the off-diagonal blocks of the FIM, since the block-diagonal approach is sufficiently robust, accurate and economical in computation time.
翻译:作为一种二阶方法,自然梯度下降具有加速神经网络训练的能力。然而,由于计算和反转费舍尔信息矩阵的计算和内存成本高昂,因此需要高效的近似方法使得自然梯度下降可扩展到深度神经网络。已有许多这样的近似尝试。其中最复杂的是KFAC,其将FIM近似为一个块对角矩阵,其中每个块对应于神经网络的一层。通过这样做,KFAC忽略了不同层之间的相互作用。本文中,我们通过两级方法的使用,研究了恢复层与层之间低频交互的意义,受领域分解的启示,提出并评估了几种不同粗粒度空间的KFAC两级校正方法。所得结果表明,以这种方式包含层间交互并不真正改善KFAC的性能。这表明块对角方法足够健壮、准确和经济,并且可以安全地丢弃FIM的非对角块。