An Efficient Frequency-Based Approach for Maximal Square Detection in Binary Matrices

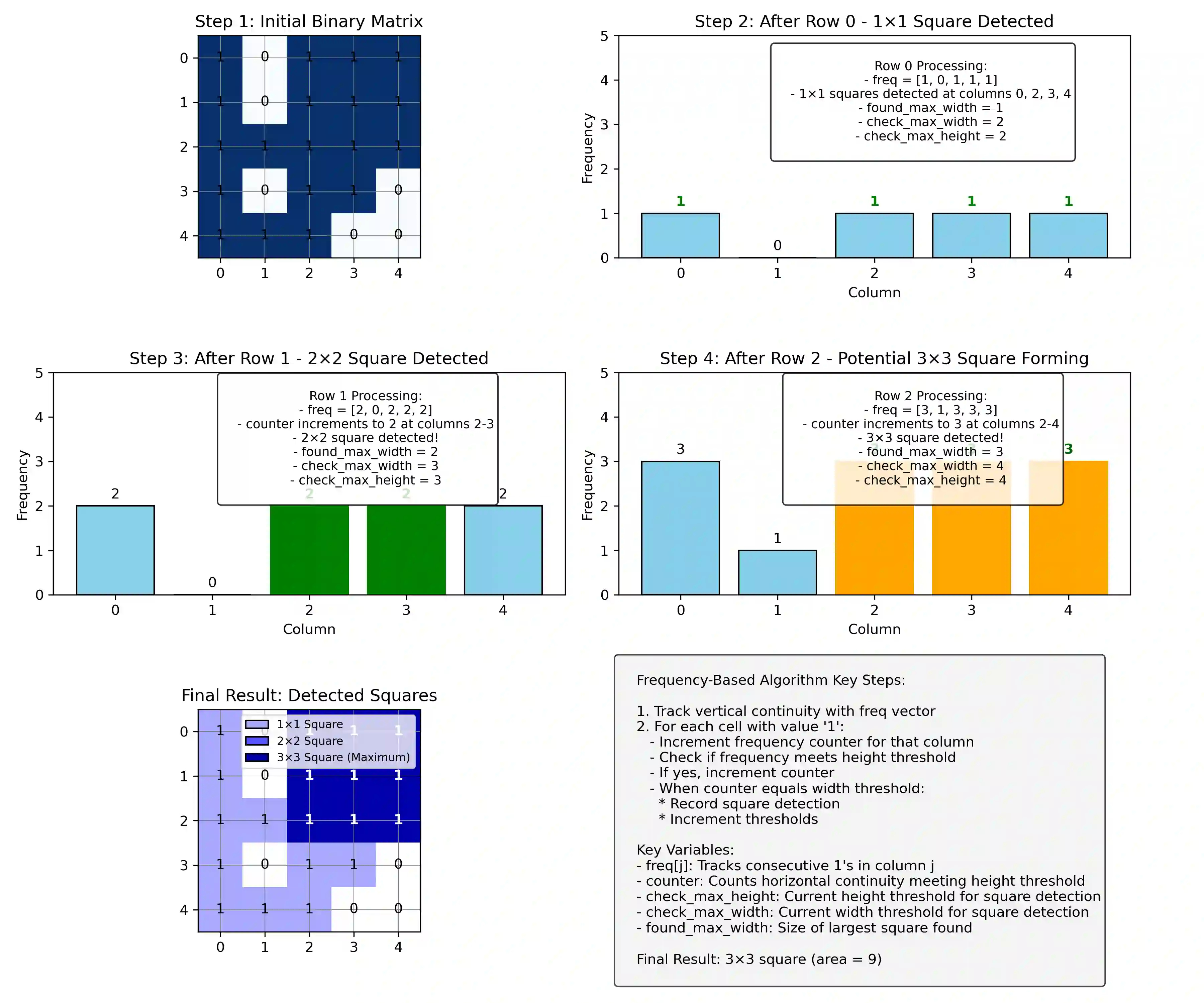
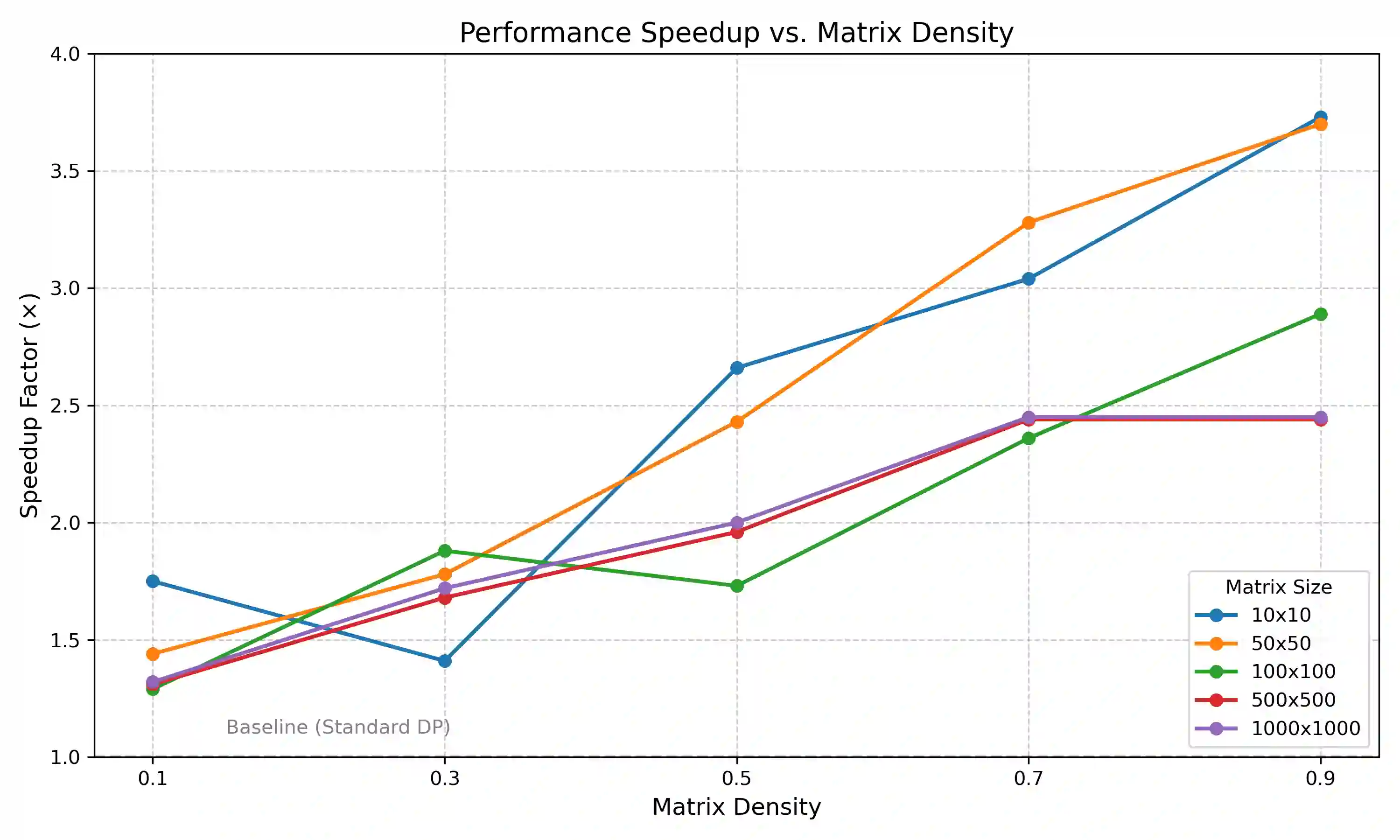
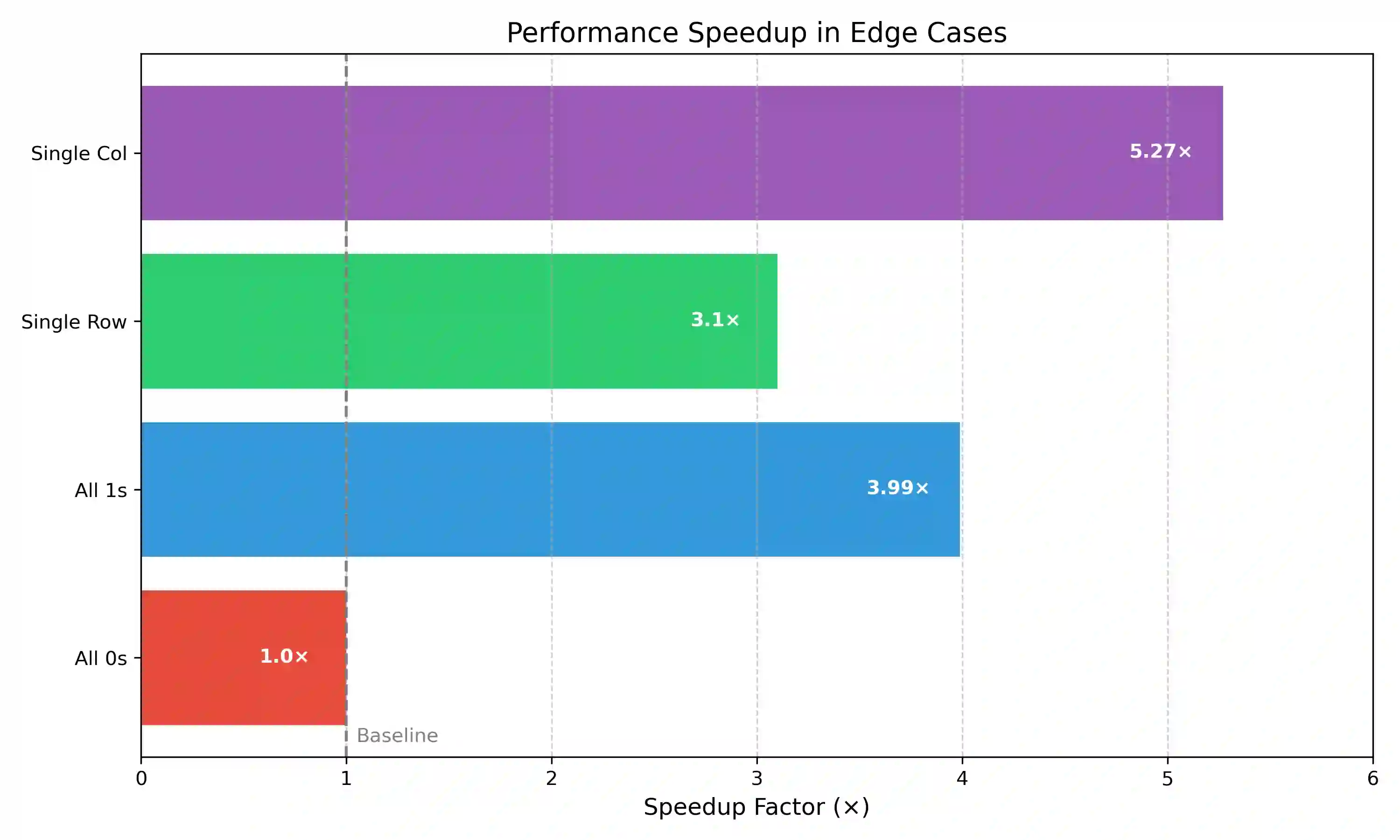
This paper presents a novel frequency-based algorithm which solves the maximal square problem with improved practical speed performance while maintaining optimal asymptotic complexity. My approach tracks the columnar continuity of ones through an adaptive frequency vector and dynamic thresholding mechanism that eliminates the need for nested minimum operations commonly found in standard dynamic programming solutions. Theoretical analysis confirms a time complexity of O(mn) and a space complexity of O(n).Formal loop-invariant proofs verify correctness, while comprehensive benchmarking demonstrates speed improvements of 1.3-5x over standard methods in various matrix densities and sizes. This method improves algorithm design and simultaneously creates opportunities for faster spatial pattern recognition in fields like urban planning, environmental science, and medical imaging.