On the (Im)Possibility of Estimating Various Notions of Differential Privacy

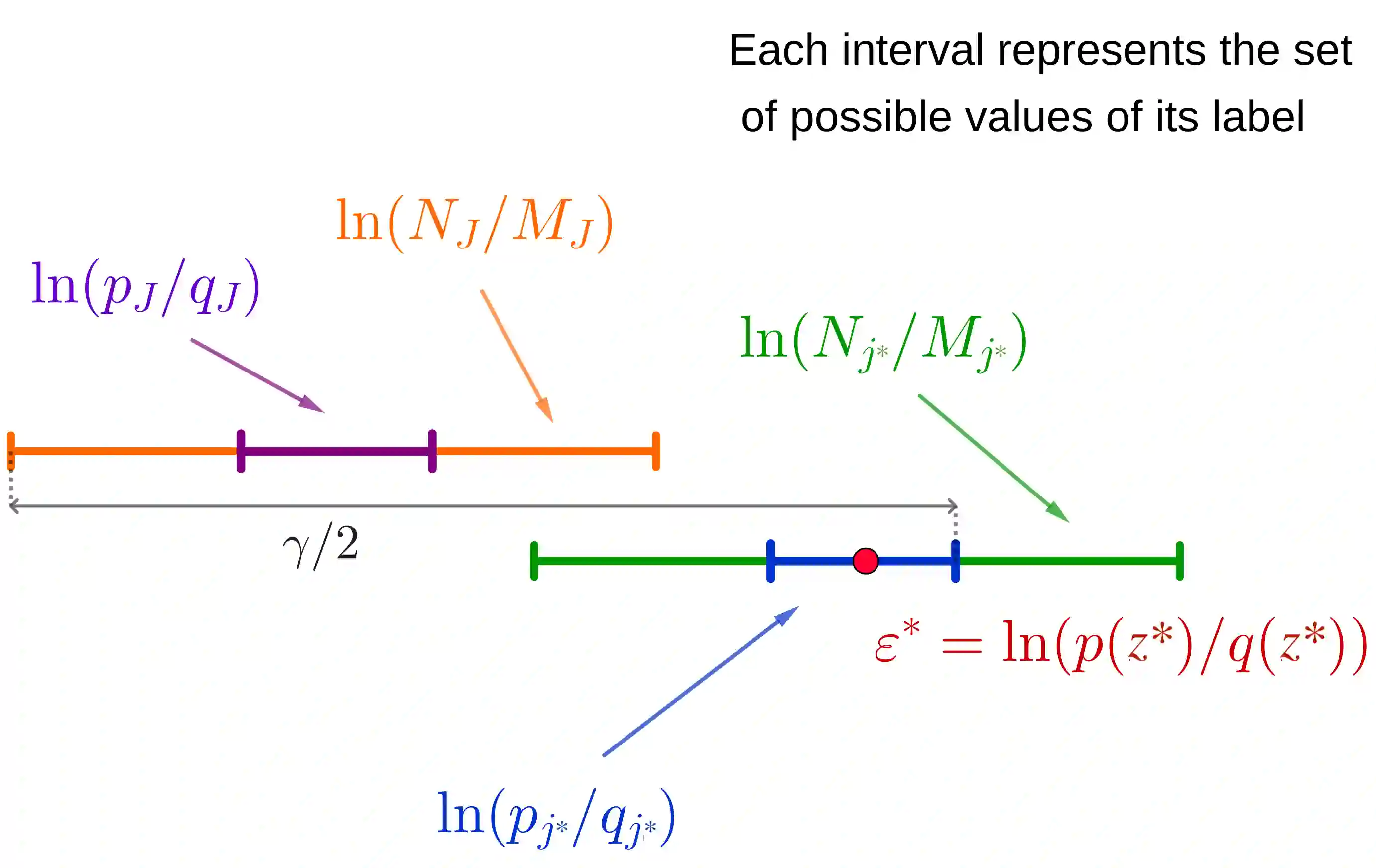
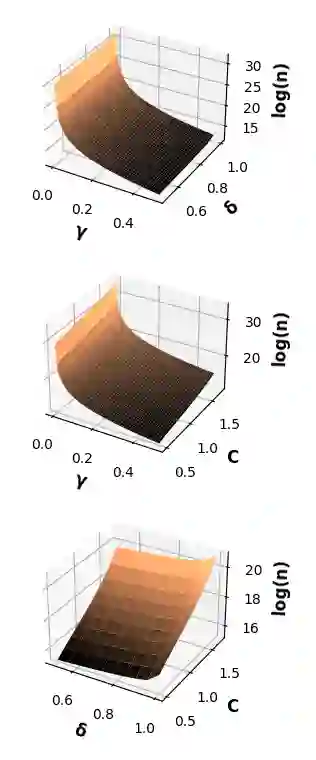
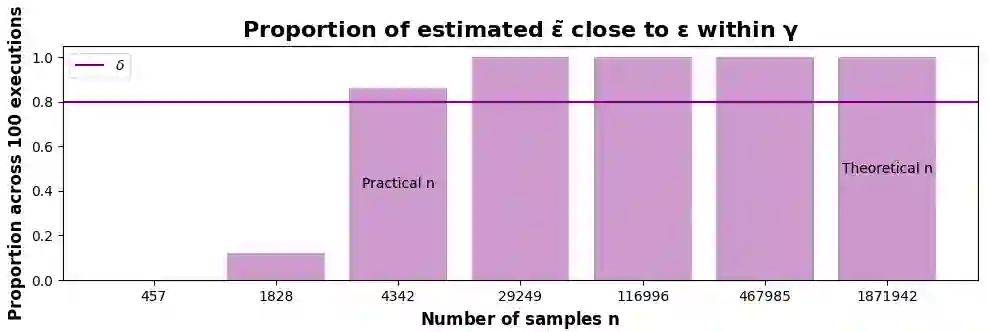
We analyze to what extent final users can infer information about the level of protection of their data when the data obfuscation mechanism is a priori unknown to them (the so-called ''black-box'' scenario). In particular, we delve into the investigation of two notions of local differential privacy (LDP), namely {\epsilon}-LDP and R\'enyi LDP. On one hand, we prove that, without any assumption on the underlying distributions, it is not possible to have an algorithm able to infer the level of data protection with provable guarantees; this result also holds for the central versions of the two notions of DP considered. On the other hand, we demonstrate that, under reasonable assumptions (namely, Lipschitzness of the involved densities on a closed interval), such guarantees exist and can be achieved by a simple histogram-based estimator. We validate our results experimentally and we note that, on a particularly well-behaved distribution (namely, the Laplace noise), our method gives even better results than expected, in the sense that in practice the number of samples needed to achieve the desired confidence is smaller than the theoretical bound, and the estimation of {\epsilon} is more precise than predicted.