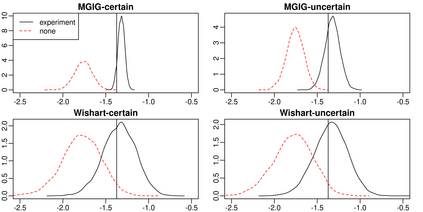
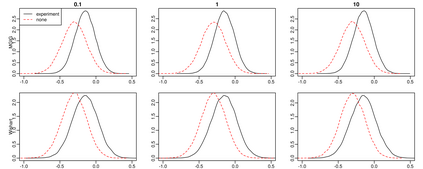
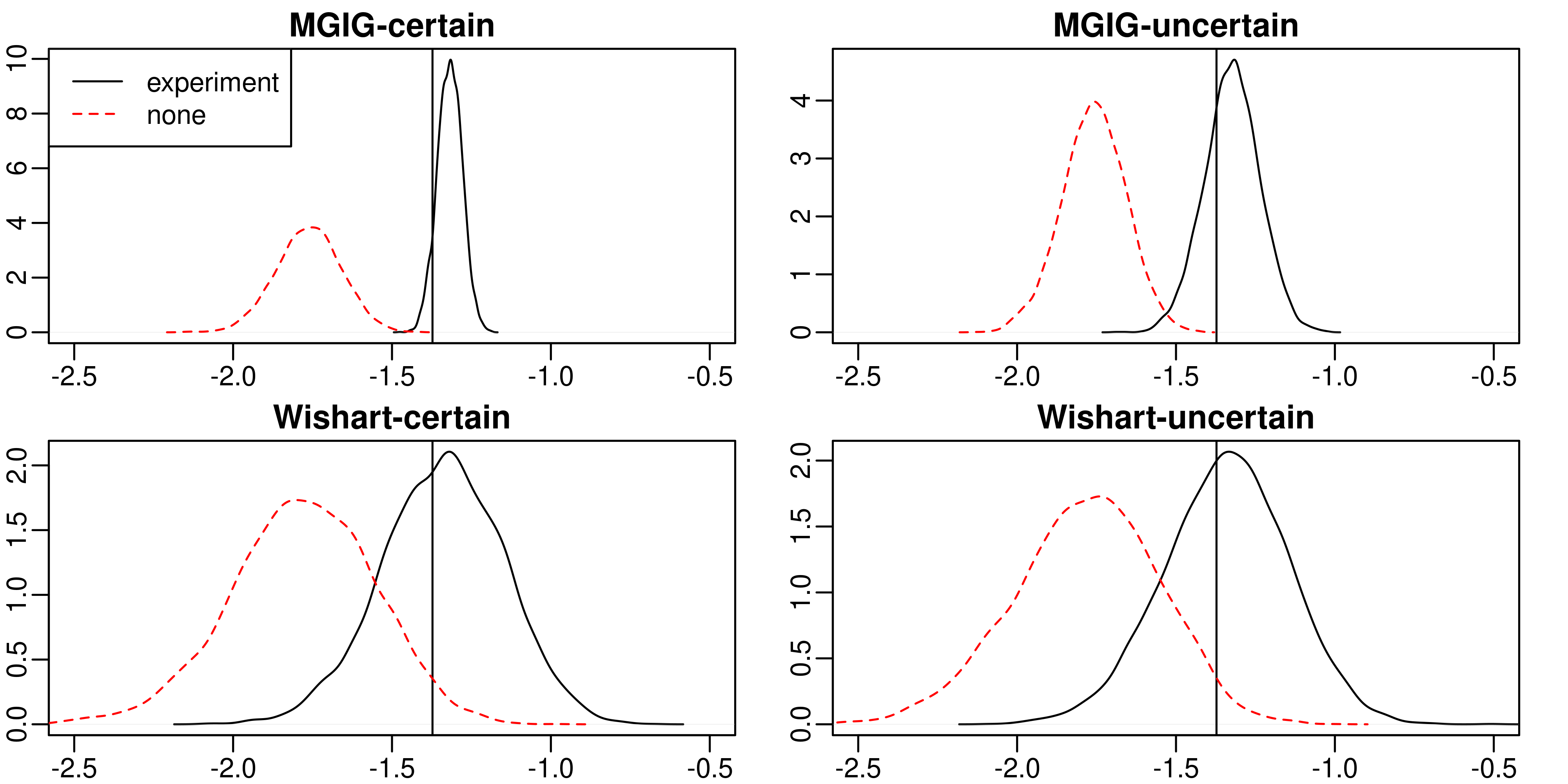
Here, we investigate whether (and how) experimental design could aid in the estimation of the precision matrix in a Gaussian chain graph model, especially the interplay between the design, the effect of the experiment and prior knowledge about the effect. Estimation of the precision matrix is a fundamental task to infer biological graphical structures like microbial networks. We compare the marginal posterior precision of the precision matrix under four priors: flat, conjugate Normal-Wishart, Normal-MGIG and a general independent. Under the flat and conjugate priors, the Laplace-approximated posterior precision is not a function of the design matrix rendering useless any efforts to find an optimal experimental design to infer the precision matrix. In contrast, the Normal-MGIG and general independent priors do allow for the search of optimal experimental designs, yet there is a sharp upper bound on the information that can be extracted from a given experiment. We confirm our theoretical findings via a simulation study comparing i) the KL divergence between prior and posterior and ii) the Stein's loss difference of MAPs between random and no experiment. Our findings provide practical advice for domain scientists conducting experiments to better infer the precision matrix as a representation of a biological network.
翻译:在这里,我们研究实验设计是否(以及如何)有助于估计高斯链图模型中的精度矩阵,特别是设计、实验效果和先验知识之间的相互作用。估计精度矩阵是推断生物图形结构(如微生物网络)的基本任务。我们将4个先验的边缘后验精度进行比较:平坦先验、共轭正态-Wishart先验、正态-MGIG先验和一般独立先验。在平坦和共轭先验下,拉普拉斯近似的后验精度不是设计矩阵的函数,无法使任何努力寻找推断精度矩阵的最佳实验设计。相反,正态-MGIG和一般独立先验允许搜索最佳的实验设计,但从给定实验中可以提取的信息有一个尖锐的上限。我们通过模拟研究来确认我们的理论发现,比较i)先验和后验之间的KL散度和ii)随机实验和无实验之间的MAPs的Stein损失差异。我们的研究为开展实验的领域科学家提供了实用建议,以更好地推断精度矩阵作为生物网络的表示。