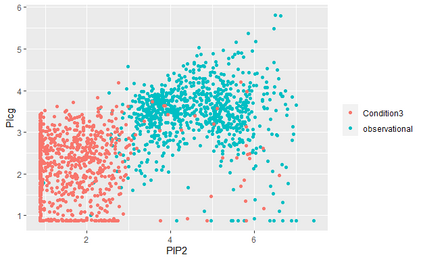
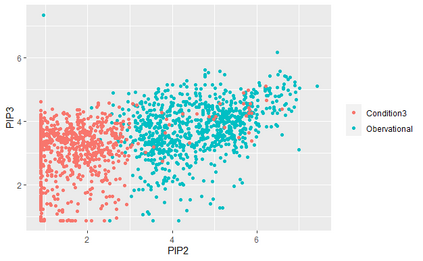
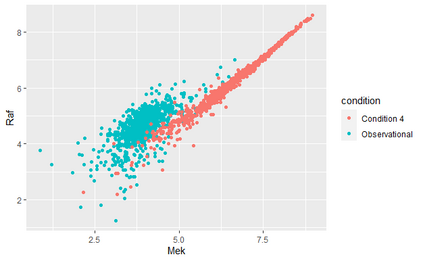
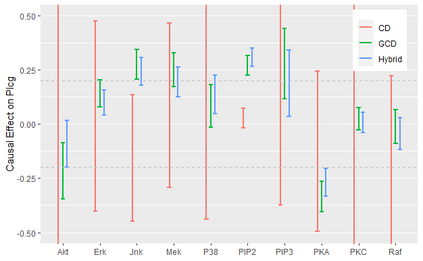
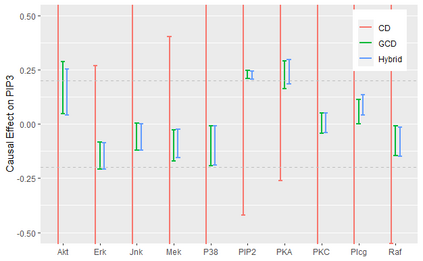
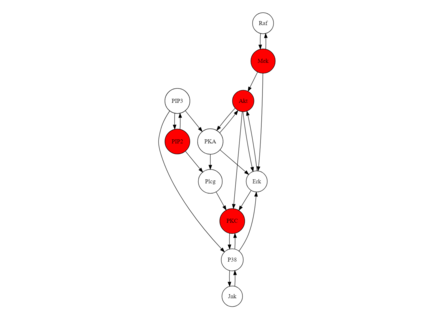
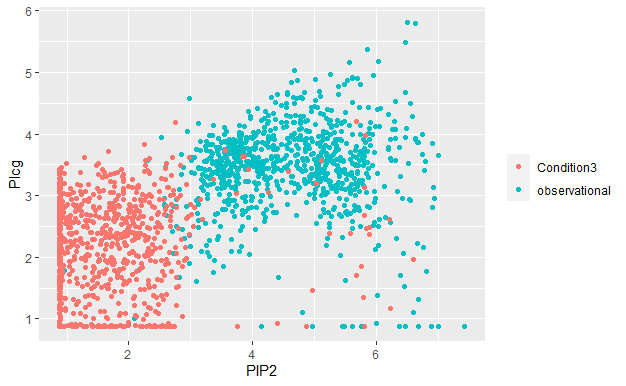
Recent works have proposed regression models which are invariant across data collection environments. These estimators often have a causal interpretation under conditions on the environments and type of invariance imposed. One recent example, the Causal Dantzig (CD), is consistent under hidden confounding and represents an alternative to classical instrumental variable estimators such as Two Stage Least Squares (TSLS). In this work we derive the CD as a generalized method of moments (GMM) estimator. The GMM representation leads to several practical results, including 1) creation of the Generalized Causal Dantzig (GCD) estimator which can be applied to problems with continuous environments where the CD cannot be fit 2) a Hybrid (GCD-TSLS combination) estimator which has properties superior to GCD or TSLS alone 3) straightforward asymptotic results for all methods using GMM theory. We compare the CD, GCD, TSLS, and Hybrid estimators in simulations and an application to a Flow Cytometry data set. The newly proposed GCD and Hybrid estimators have superior performance to existing methods in many settings.
翻译:暂无翻译