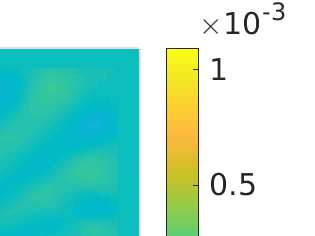
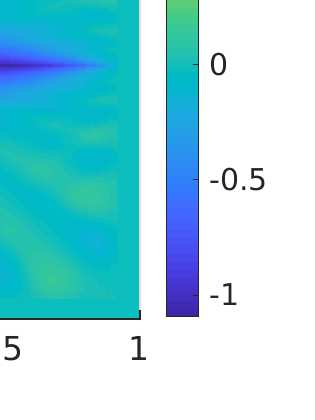
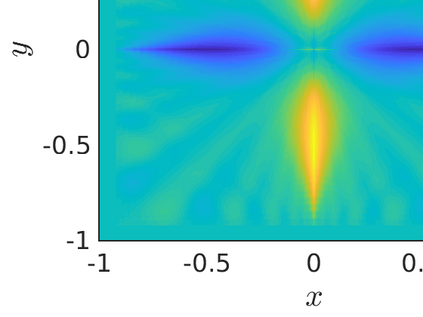
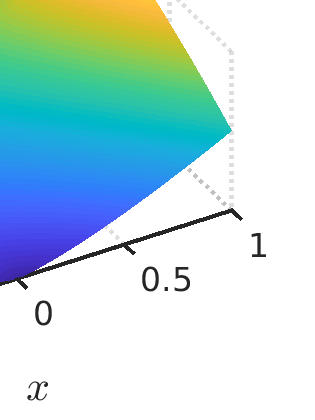
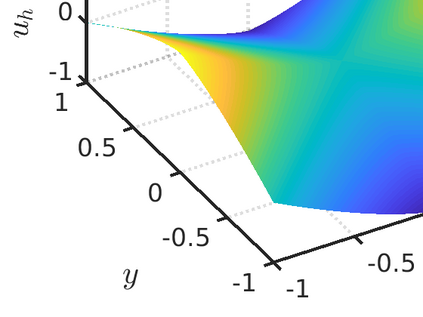
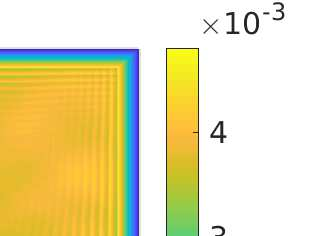
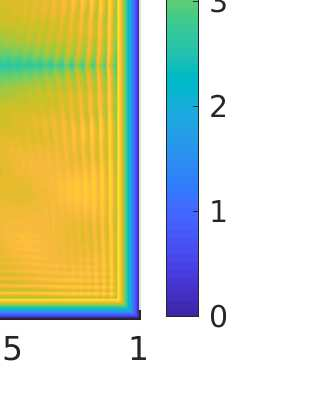
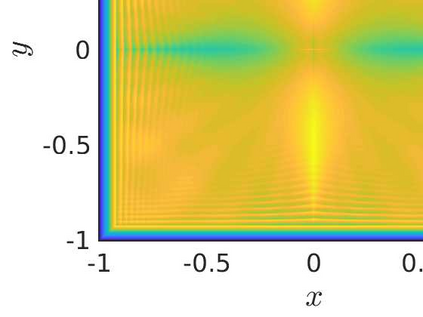
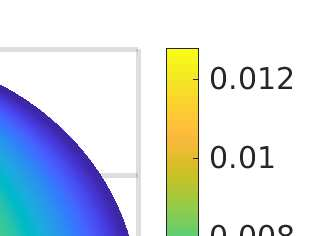
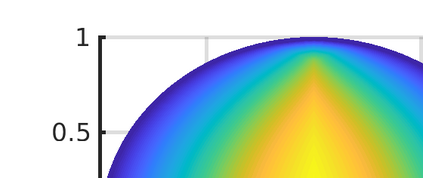
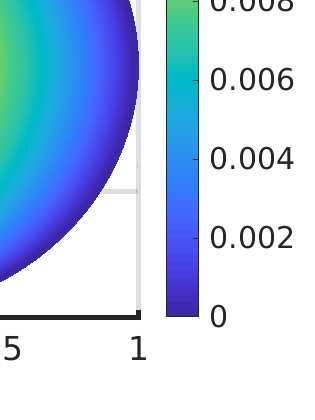
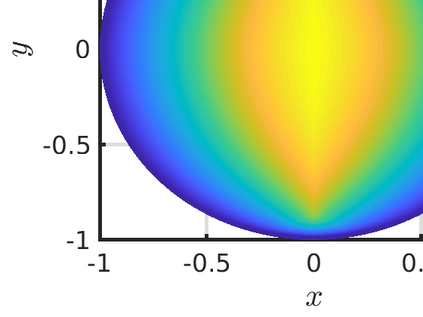
We propose a monotone, and consistent numerical scheme for the approximation of the Dirichlet problem for the normalized Infinity Laplacian, which could be related to the family of so--called two--scale methods. We show that this method is convergent, and prove rates of convergence. These rates depend not only on the regularity of the solution, but also on whether or not the right hand side vanishes. Some extensions to this approach, like obstacle problems and symmetric Finsler norms are also considered.
翻译:我们提出了一个单调和一致的数值方案,以近似Drichlet问题,解决标准化的无限拉普拉西亚问题,它可能与所谓的双尺度方法的家庭有关。我们表明,这种方法是趋同的,并证明趋同率。这些比率不仅取决于解决办法的规律性,而且取决于右手侧是否消失。 这种方法的一些延伸,如障碍问题和芬斯勒对称规范,也会得到考虑。
相关内容
专知会员服务
54+阅读 · 2020年1月30日
专知会员服务
36+阅读 · 2019年10月17日
Arxiv
0+阅读 · 2022年10月24日
Arxiv
0+阅读 · 2022年10月23日
Arxiv
0+阅读 · 2022年10月21日
Arxiv
0+阅读 · 2022年10月20日
Arxiv
0+阅读 · 2022年10月20日
Arxiv
0+阅读 · 2022年10月20日