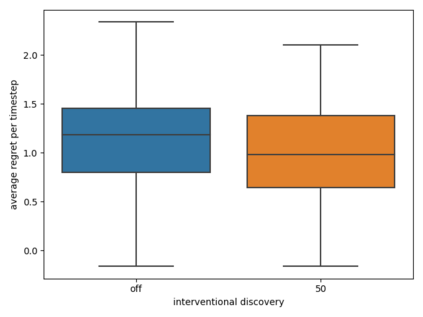
We explore how observational and interventional causal discovery methods can be combined. A state-of-the-art observational causal discovery algorithm for time series capable of handling latent confounders and contemporaneous effects, called LPCMCI, is extended to profit from casual constraints found through randomized control trials. Numerical results show that, given perfect interventional constraints, the reconstructed structural causal models (SCMs) of the extended LPCMCI allow 84.6% of the time for the optimal prediction of the target variable. The implementation of interventional and observational causal discovery is modular, allowing causal constraints from other sources. The second part of this thesis investigates the question of regret minimizing control by simultaneously learning a causal model and planning actions through the causal model. The idea is that an agent to optimize a measured variable first learns the system's mechanics through observational causal discovery. The agent then intervenes on the most promising variable with randomized values allowing for the exploitation and generation of new interventional data. The agent then uses the interventional data to enhance the causal model further, allowing improved actions the next time. The extended LPCMCI can be favorable compared to the original LPCMCI algorithm. The numerical results show that detecting and using interventional constraints leads to reconstructed SCMs that allow 60.9% of the time for the optimal prediction of the target variable in contrast to the baseline of 53.6% when using the original LPCMCI algorithm. Furthermore, the induced average regret decreases from 1.2 when using the original LPCMCI algorithm to 1.0 when using the extended LPCMCI algorithm with interventional discovery.
翻译:我们探索如何将观察和干预性因果关系发现方法结合起来。 能够处理潜伏混淆和当期效应的时间序列的最新观察性因果关系发现算法,称为LPCMCI,被扩展为通过随机控制试验从随机控制试验发现的偶然限制中获益。 数值结果显示,鉴于完美的干预限制,扩展的LPCMCI的重建结构性因果模型(SCM)允许84.6%的时间最佳预测目标变量。 实施干预性和观察性因果关系发现是模块化的,允许其他来源的因果限制。 这部分的第二部分通过同时学习因果模型和通过因果模型规划行动来调查尽量减少控制遗憾的问题。 概念是, 一个优化可计量变量的代理通过观察性因果发现先了解系统的机械学。 代理随后对最有前途的变量进行干预, 随机值允许利用新的干预数据。 代理方随后使用干预性数据进一步强化因果模型,允许下期行动得到改进。 扩展的LPCIMILMCI 使用成本性指标性指标,然后在使用最初的逻辑性评估结果时, 将LMCI 和逻辑性指标性指标性指标性指标性指标性比再用前的逻辑性逻辑性分析。 当使用60 显示原的逻辑性逻辑性逻辑性分析后, 将LPC 将LMC的逻辑性指标性调整后, 将LMCI 以最佳的逻辑性逻辑性比为最佳的逻辑性指标性比值值值值 。