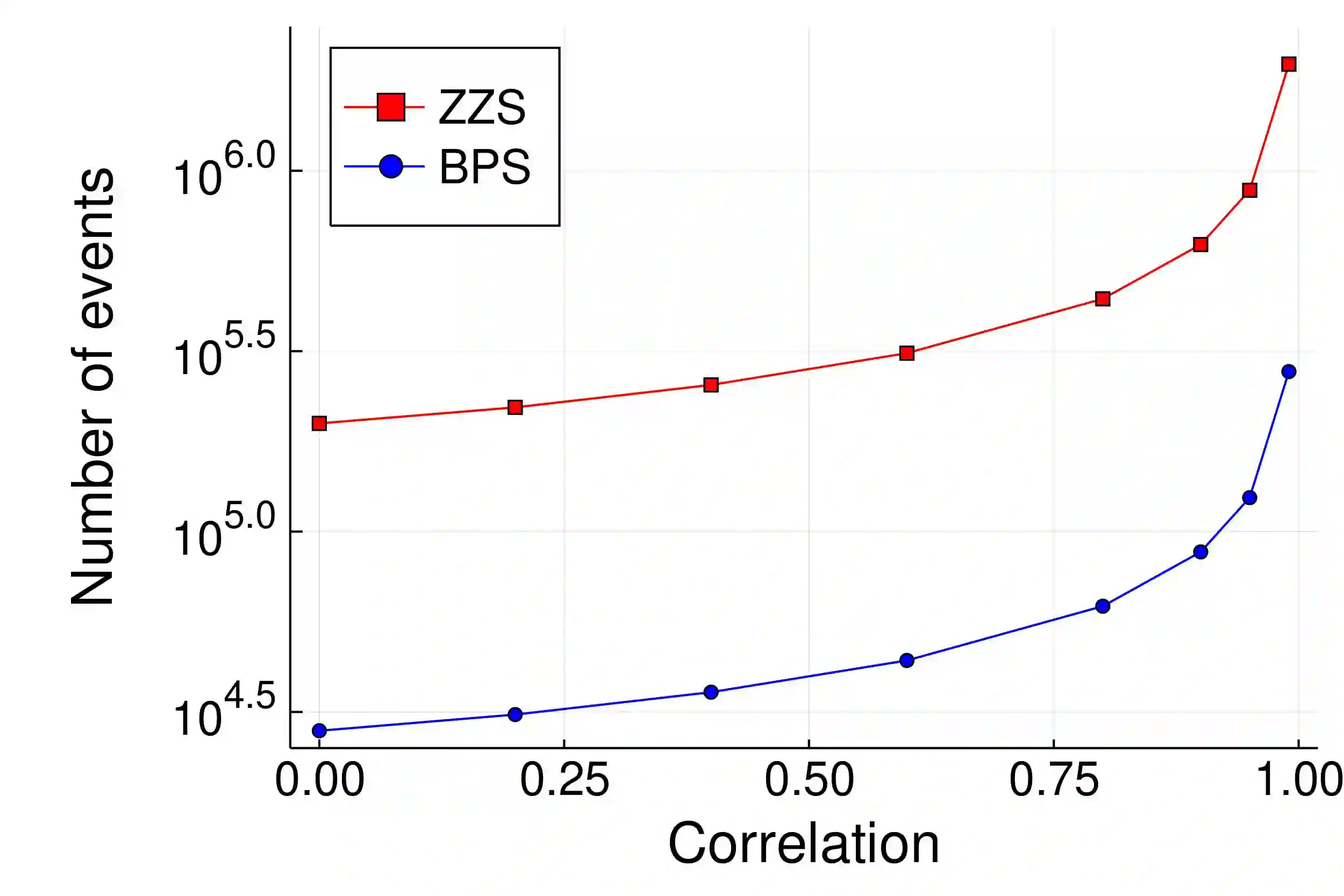
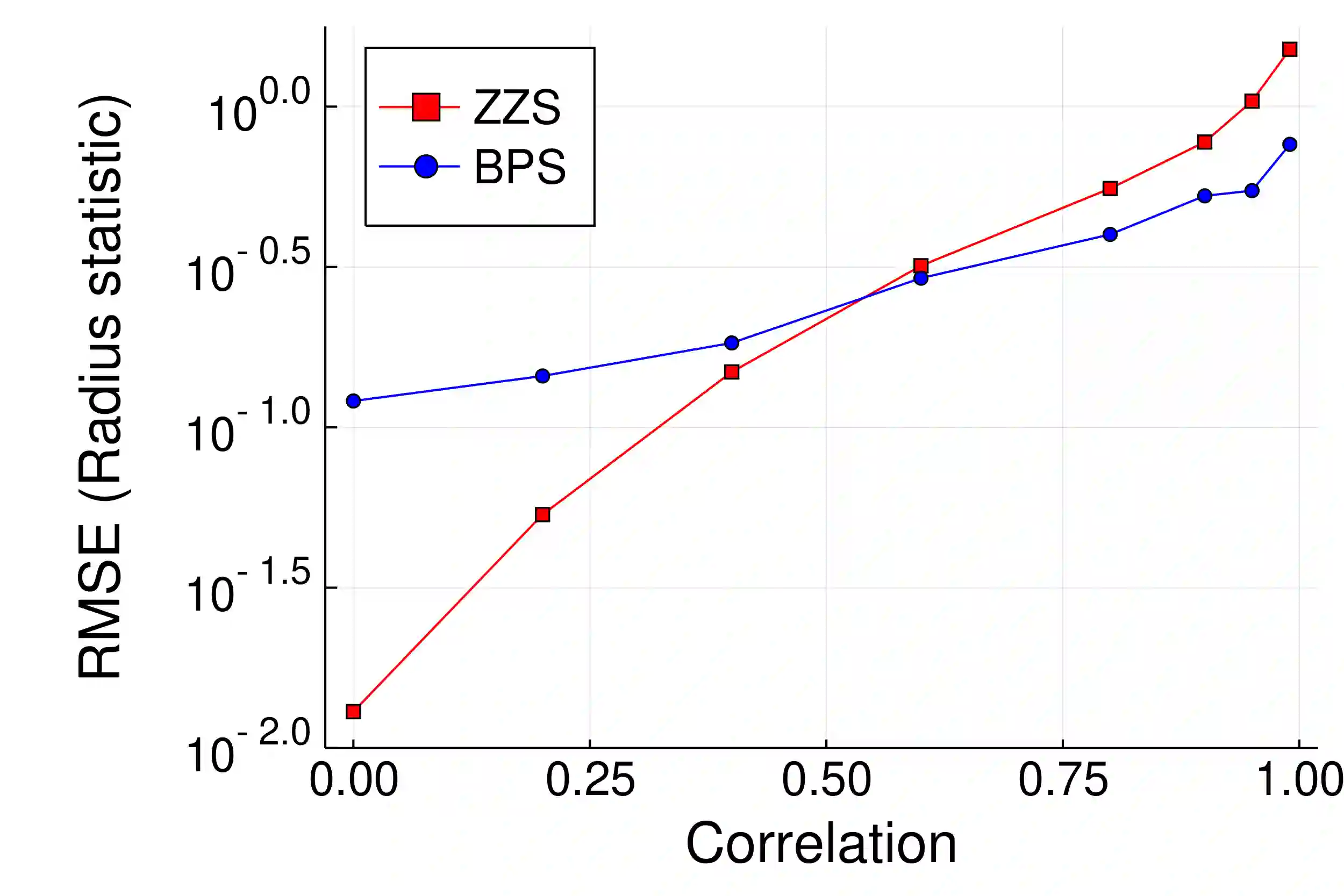
The Bouncy Particle sampler (BPS) and the Zig-Zag sampler (ZZS) are continuous time, non-reversible Monte Carlo methods based on piecewise deterministic Markov processes. Experiments show that the speed of convergence of these samplers can be affected by the shape of the target distribution, as for instance in the case of anisotropic targets. We propose an adaptive scheme that iteratively learns all or part of the covariance matrix of the target and takes advantage of the obtained information to modify the underlying process with the aim of increasing the speed of convergence. Moreover, we define an adaptive scheme that automatically tunes the refreshment rate of the BPS or ZZS. We prove ergodicity and a law of large numbers for all the proposed adaptive algorithms. Finally, we show the benefits of the adaptive samplers with several numerical simulations.
翻译:实验表明,这些取样器的趋同速度可能受到目标分布形状的影响,例如,在厌异性目标的情况下。我们提出了一个适应性办法,即反复学习目标的全部或部分共变矩阵,并利用所获得的信息修改基本过程,以便加快趋同速度。此外,我们定义了一种适应性办法,自动调和BPS或ZZS的恢复速度。我们证明所有拟议的适应性算法都是主观的,并且有较大数量的法律。最后,我们用若干数字模拟来展示适应性取样器的好处。