Assessing the goodness of fit of linear regression via higher-order least squares

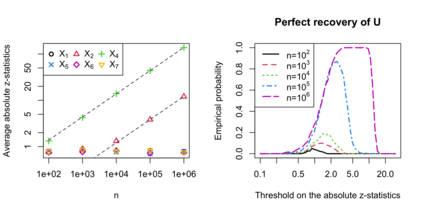
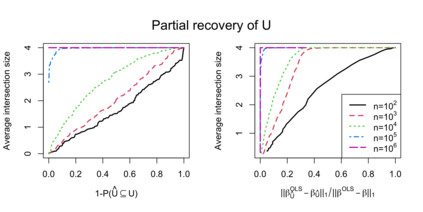
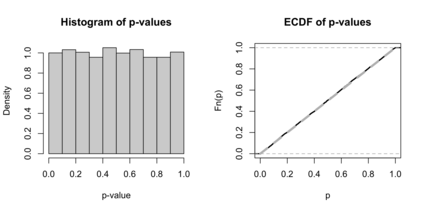
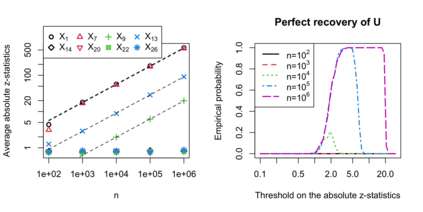
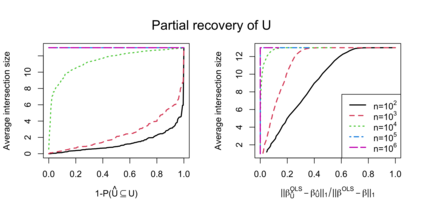
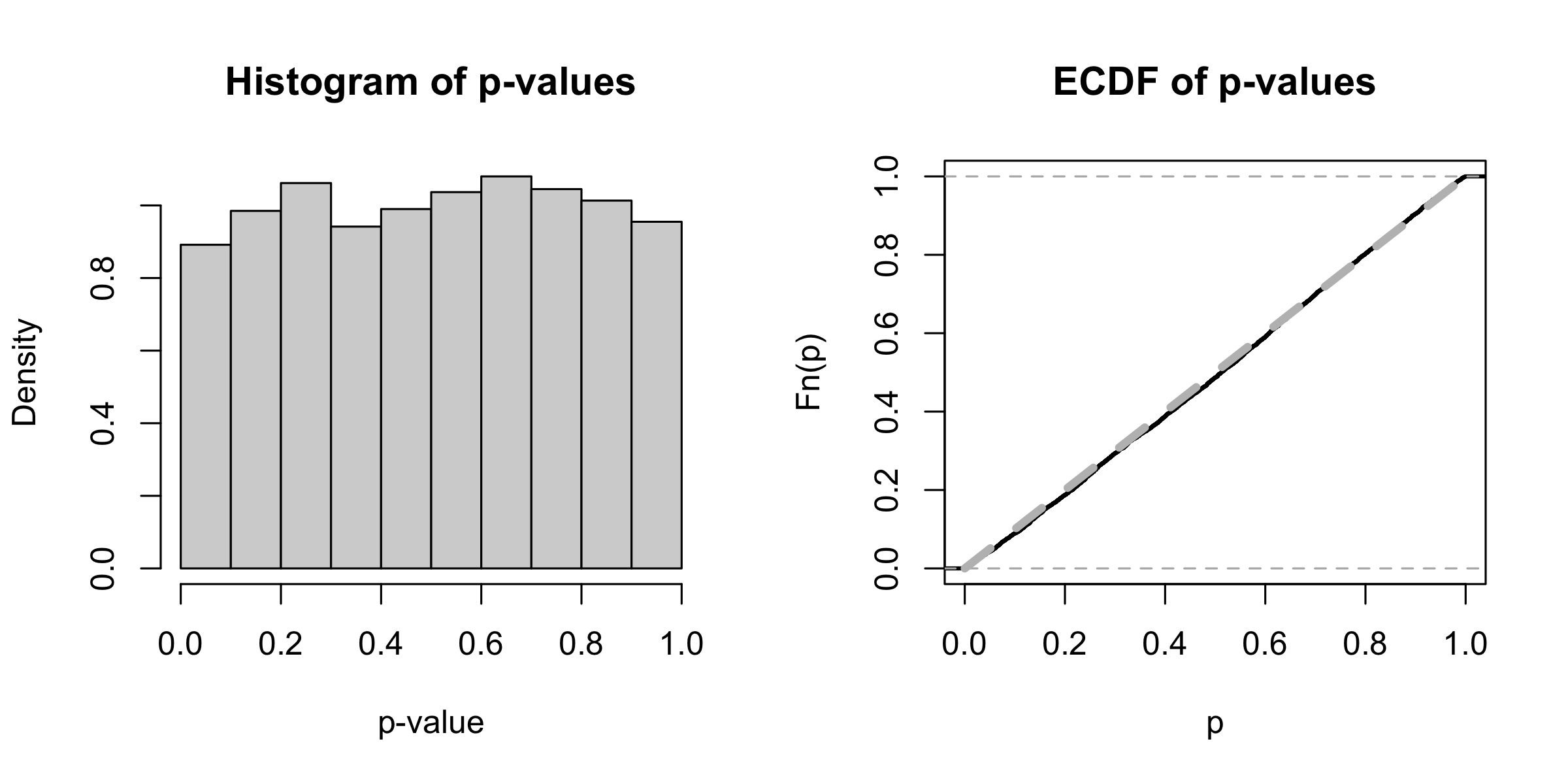
We introduce a simple diagnostic test for assessing the goodness of fit of linear regression, and in particular for detecting hidden confounding. We propose to evaluate the sensitivity of the regression coefficient with respect to changes of the marginal distribution of covariates by comparing the so-called higher-order least squares with the usual least squares estimates. In spite of its simplicity, this strategy is extremely general and powerful. Specifically, we show that it allows to distinguish between confounded and unconfounded predictor variables as well as determining ancestor variables in structural equation models.