Count-Free Weisfeiler--Leman and Group Isomorphism

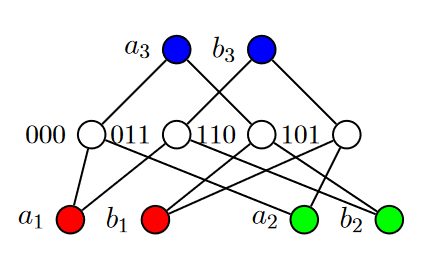
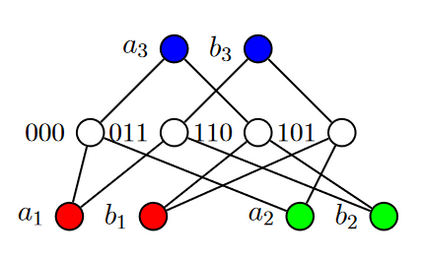
We investigate the power of counting in \textsc{Group Isomorphism}. We first leverage the count-free variant of the Weisfeiler--Leman Version I algorithm for groups (Brachter & Schweitzer, LICS 2020) in tandem with limited non-determinism and limited counting to improve the parallel complexity of isomorphism testing for several families of groups. In particular, we show the following: - Let $G_{1}$ and $G_{2}$ be class $2$ $p$-groups of exponent $p$ arising from the CFI and twisted CFI graphs (Cai, F\"urer, & Immerman, Combinatorica 1992) respectively, via Mekler's construction (J. Symb. Log., 1981). If the base graph $\Gamma_{0}$ is $3$-regular and connected, then we can distinguish $G_{1}$ from $G_{2}$ in $\beta_{1}\textsf{MAC}^{0}(\textsf{FOLL})$. This improves the upper bound of $\textsf{TC}^{1}$ from Brachter & Schweitzer (ibid). - Isomorphism testing between an arbitrary group $K$ and a group $G$ with an Abelian normal Hall subgroup whose complement is an $O(1)$-generated solvable group with solvability class poly $\log \log n$ is in $\beta_{1}\textsf{MAC}^{0}(\textsf{FO}($poly $\log \log n))$. This notably includes instances where the complement is an $O(1)$-generated nilpotent group. This problem was previously known to be in $\textsf{P}$ (Qiao, Sarma, & Tang, STACS 2011) and $\textsf{L}$ (Grochow & Levet, arXiv 2022). - Isomorphism testing between a direct product of simple groups and an arbitrary group is in $\beta_{1} \textsf{MAC}^{0}(\textsf{FOLL})$. This problem was previously shown to be in $\textsf{L}$ (Brachter & Schweitzer, ESA 2022). We finally show that the $q$-ary count-free pebble game is unable to distinguish even Abelian groups. This extends the result of Grochow & Levet (arXiv 2022), who established the result in the case of $q = 1$. The general theme is that some counting appears necessary to place \textsc{Group Isomorphism} into $\textsf{P}$.