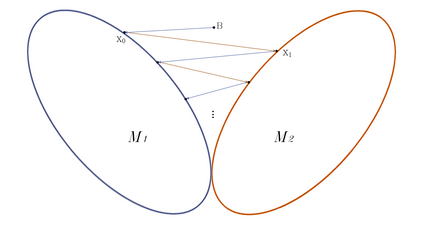
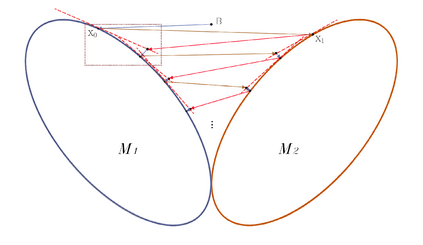
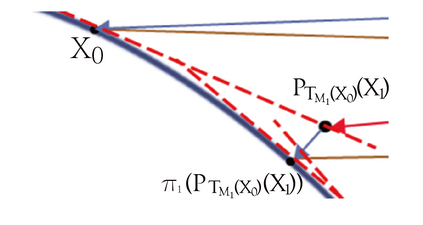
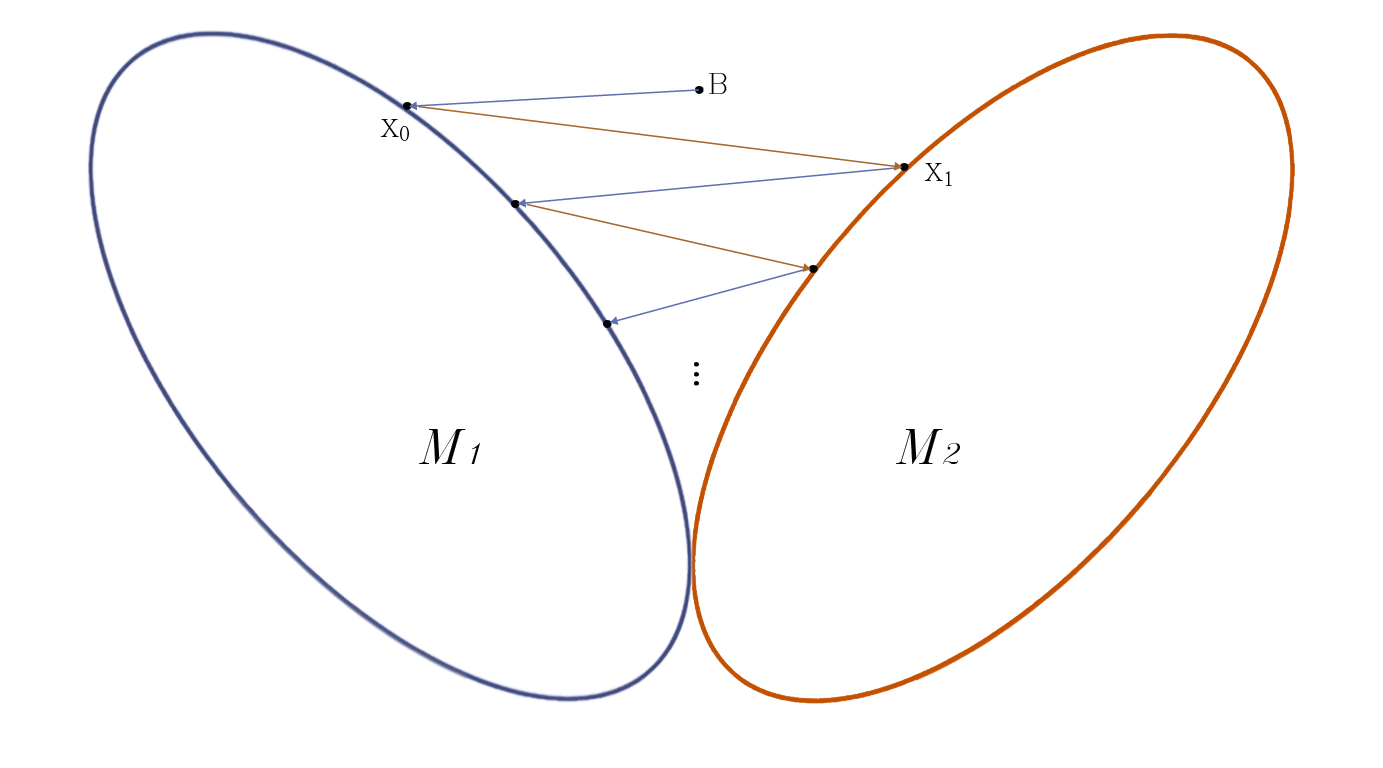
In this paper, we study alternating projections on nontangential manifolds based on the tangent spaces. The main motivation is that the projection of a point onto a manifold can be computational expensive. We propose to use the tangent space of the point in the manifold to approximate the projection onto the manifold in order to reduce the computational cost. We show that the sequence generated by alternating projections on two nontangential manifolds based on tangent spaces, converges linearly to a point in the intersection of the two manifolds where the convergent point is close to the optimal solution. Numerical examples for nonnegative low rank matrix approximation and low rank image quaternion matrix (color image) approximation, are given to demonstrate that the performance of the proposed method is better than that of the classical alternating projection method in terms of computational time.
翻译:在本文中,我们根据偏差空格研究非切差方块的交替预测。 主要的动机是, 向一个元点投射可能是计算费用昂贵的。 我们提议使用方块点的相切空间来估计投向方块的相近度, 以减少计算成本。 我们显示,基于偏差空格对两个非切差方块的交替预测所产生的顺序, 线性地汇合到两个方块交叉点的点上, 其中汇合点接近于最佳的解决方案。 给出非负性低级矩阵近似和低级图像偏差矩阵( 彩色图像)近似值的数值示例, 以表明拟议方法的性能优于计算时间的经典交替投影法。