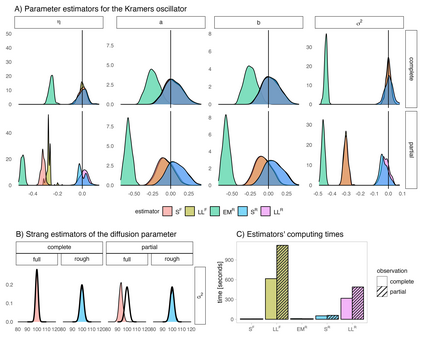
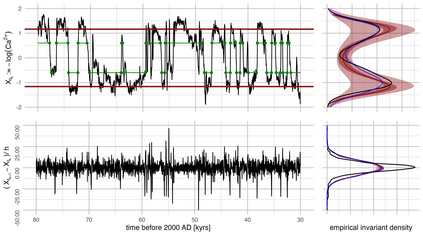
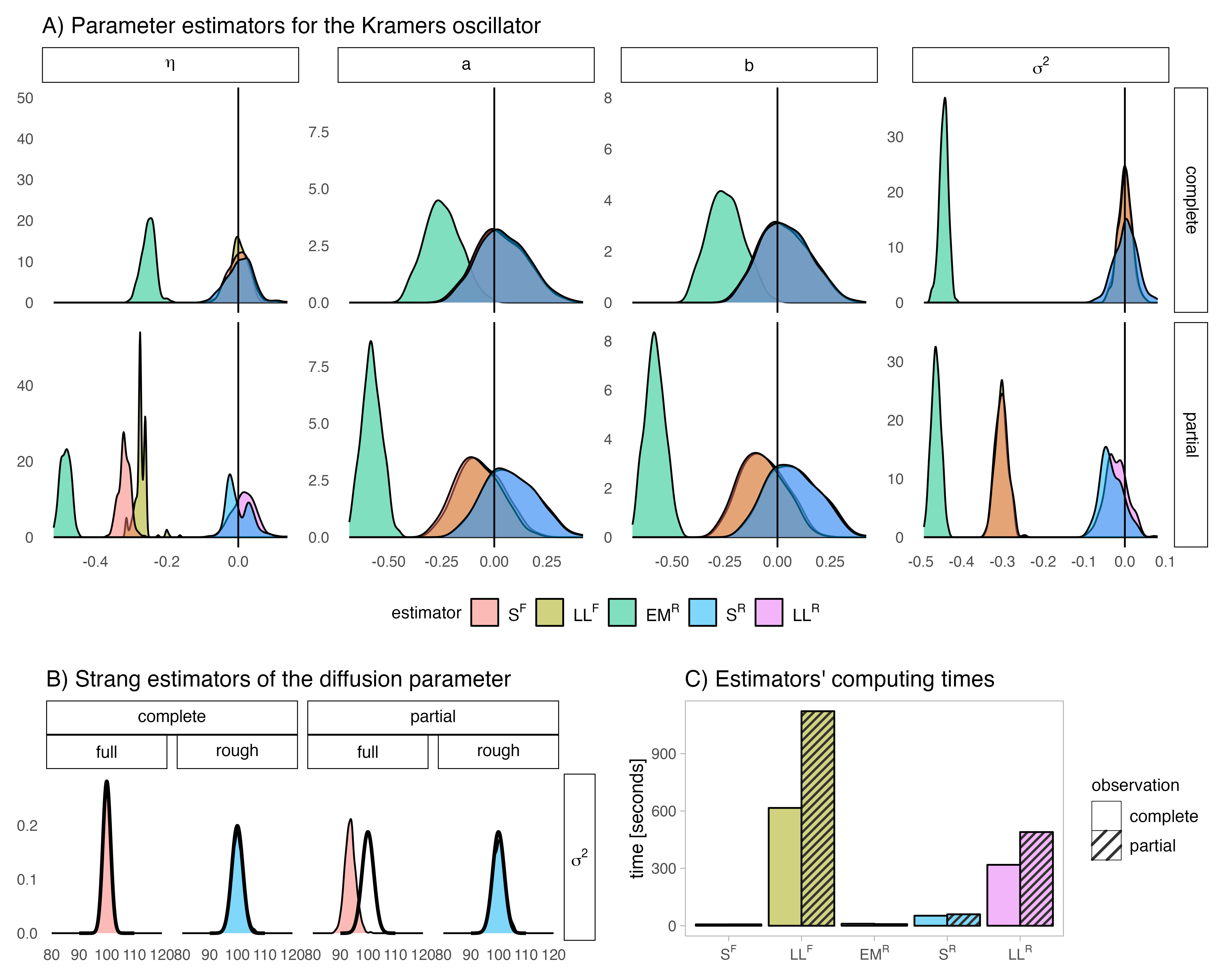
We address parameter estimation in second-order stochastic differential equations (SDEs), prevalent in physics, biology, and ecology. Second-order SDE is converted to a first-order system by introducing an auxiliary velocity variable raising two main challenges. First, the system is hypoelliptic since the noise affects only the velocity, making the Euler-Maruyama estimator ill-conditioned. To overcome that, we propose an estimator based on the Strang splitting scheme. Second, since the velocity is rarely observed we adjust the estimator for partial observations. We present four estimators for complete and partial observations, using full likelihood or only velocity marginal likelihood. These estimators are intuitive, easy to implement, and computationally fast, and we prove their consistency and asymptotic normality. Our analysis demonstrates that using full likelihood with complete observations reduces the asymptotic variance of the diffusion estimator. With partial observations, the asymptotic variance increases due to information loss but remains unaffected by the likelihood choice. However, a numerical study on the Kramers oscillator reveals that using marginal likelihood for partial observations yields less biased estimators. We apply our approach to paleoclimate data from the Greenland ice core and fit it to the Kramers oscillator model, capturing transitions between metastable states reflecting observed climatic conditions during glacial eras.
翻译:暂无翻译