为什么回归问题用MSE？

文 | Matrix.小泽直树

最近在看李沐的实用机器学习课程，讲到regression问题的loss的时候有弹幕问：“为什么要平方？”如果是几年前学生问我这个问题，我会回答：“因为做回归的时候的我们的残差有正有负，取个平方求和以后可以很简单的衡量模型的好坏。同时因为平方后容易求导数，比取绝对值还要分情况讨论好用。”

但是经过了几年的科研以后，我觉得这样的回答太过于经验性了，一定会有什么更有道理的解释，于是在知乎上搜了搜。

《CC思SS：回归模型中的代价函数应该用MSE还是MAE^[1]》 这篇文章中提到MSE对于偏差比较大的数据惩罚得比较多，但是会被outlier影响，同时MSE的优化目标是平均值，而MAE的优化目标是中位数。即如果我们的数据集足够大，对于同一个x会有多个y，MSE的目标是尽可能让我们的预测值接近这些y的平均值。同时这篇文章还提到在做gradient descent的时候，MSE的梯度可以在越接近最小值的地方越平缓，这样不容易步子扯大了。而MAE的梯度一直不变，得手动调整learning rate。

《在回归问题中，为何对MSE损失的最小化等效于最大似然估计？^[2]》而这个问题里有人提到“根据中心极限定理，误差服从正态分布，此时使得样本似然函数最大等价于使得MSE最小。” 这段话引起了我的兴趣，在查阅了一些英文资料以后发现这是来自于花书的结论（Ian的《Deep Learning》）。

以下解释来源于花书（5.5）和[这篇博客]^[3]

要弄懂为什么回归问题要用MSE，首先要先明白什么是极大似然估计MLE（Maximum Likelihood Estimation）。

极大似然估计MLE

用一个一维的数据来讲解MLE的过程，假设我们有一组数据，我们假设它服从正态分布，我们的目的是：找到一组正态分布的均值和方差，使得在这套正态分布的均值方差下，我们观测到这批数据的概率最大。

手上的数据

关于这组数据，我们先胡乱地猜测一下它符合的正态分布如下：

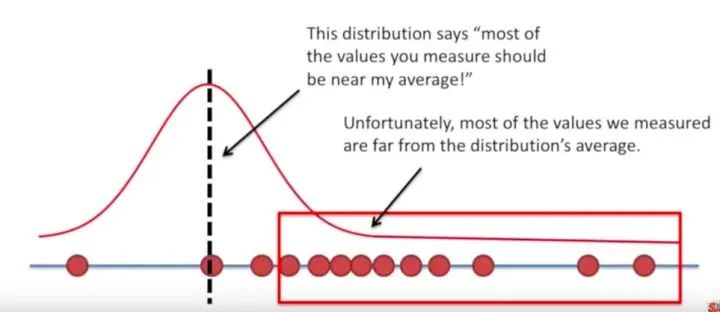
胡乱猜测的正态分布

对于这个正态分布，我们可以计算每个点出现的概率： 。其中 和 是这个正态分布的均值和方差， 是第 条数据，我们把每条数据出现的概率相乘，得到了“在这套正态分布的均值方差下，我们观测到这批数据的概率”。

同样的，我们可以猜测另一种正态分布：

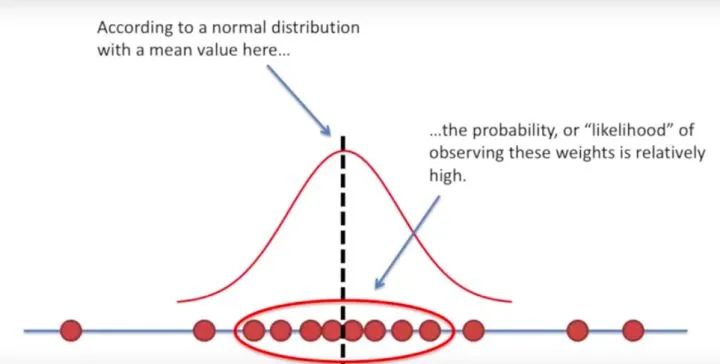
另一种猜测的正态分布

同样的，我们可以计算“在这套正态分布的均值方差下，我们观测到这批数据的概率”。

最后，我们在这群待选的均值和方差中，选出那个能使我们观测到这批数据的概率最大的均值和方差。也就是我们在做

回归问题

现在我们再看回归问题，对于回归问题来说，我们的目标不是去找一个x的正态分布了。对于一个回归问题，我们以最简单的线性回归举例。对于一个回归问题，我们的目标是 ，其中 和 是模型的参数，而 是噪声，我们假设噪声符合正态分布 。

那么我们的 其实也可以看成符合正态分布（并不是严谨的写法） ，其中 其实就是模型的预测值，也就是说 。

正态分布的probability density function是 ，带入得到。

那么也就是说，如果我们想最大化我们观测到的 的情况的话，我们应该最大化上面这个pdf的连乘结果。注意到这个值由一个常数乘上一个 的次方项，优化的时候常数项可以忽略。

于是我们的目标变成了 ，这里出现了连乘，又出现了 的次方项，很正常的想到取log，于是变成了 ，忽略常数项，稍微整理一下得到 。

于是我们就证明了，我们在做线性回归的时候，我们如果假设我们的噪声符合高斯分布，那么我们的目标函数就是MSE。

总结

很多时候，一些基础知识可能会影响你对一个模型结果表现的理解，如果对这种基础知识没有概念的话，深度学习就变成了瞎调模型瞎调参数了。[另一篇博客]^[4]就提到了，在做super resolution的时候，如果用MSE，做出来的图片会非常的模糊，就是因为MSE是基于高斯分布假设，最后的结果会尽可能地靠近高斯分布最高的地方，使得结果不会太sharp。以后还是得适时提高深度学习的理论基础。

后台回复关键词【入群】

加入卖萌屋NLP/IR/Rec与求职讨论群

后台回复关键词【顶会】

获取ACL、CIKM等各大顶会论文集！

 

[1] CC思SS：回归模型中的代价函数应该用MSE还是MAE
https://zhuanlan.zhihu.com/p/45790146

[2] 在回归问题中，为何对MSE损失的最小化等效于最大似然估计？
https://www.zhihu.com/question/426901520

[3] https://link.zhihu.com/?target=https%3A//towardsdatascience.com/where-does-mean-squared-error-mse-come-from-2002bbbd7806

[4] https://link.zhihu.com/?target=https%3A//towardsdatascience.com/mse-is-cross-entropy-at-heart-maximum-likelihood-estimation-explained-181a29450a0b