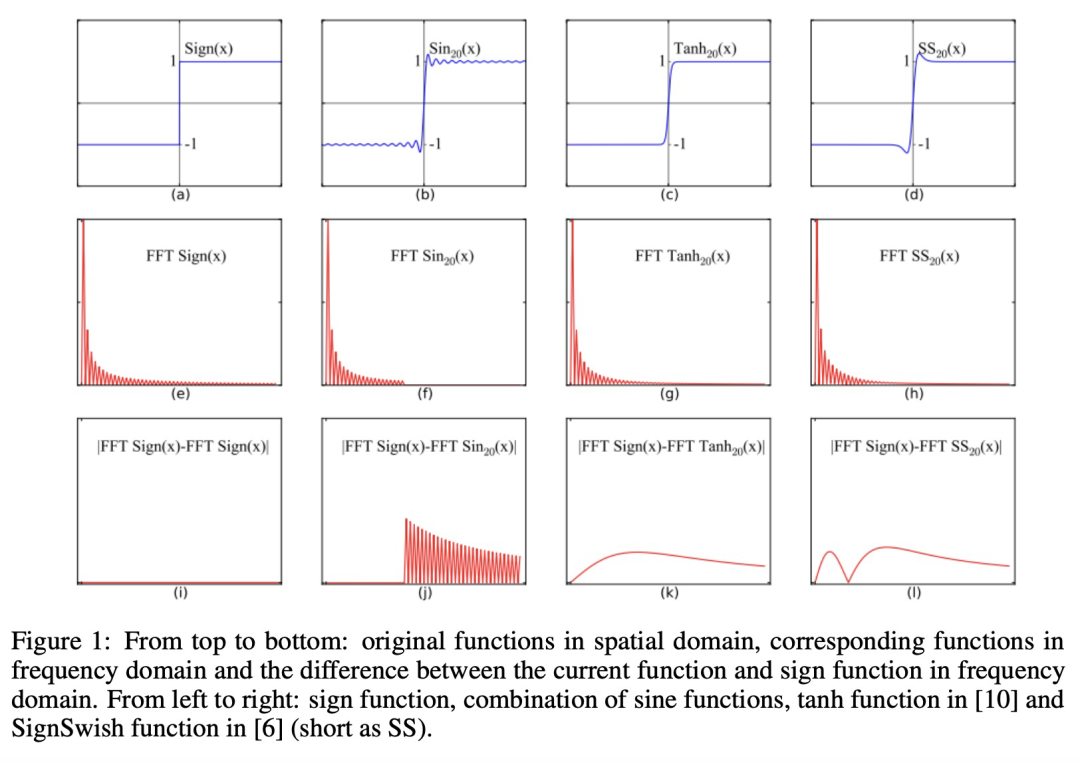
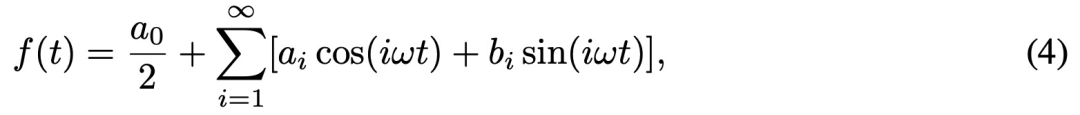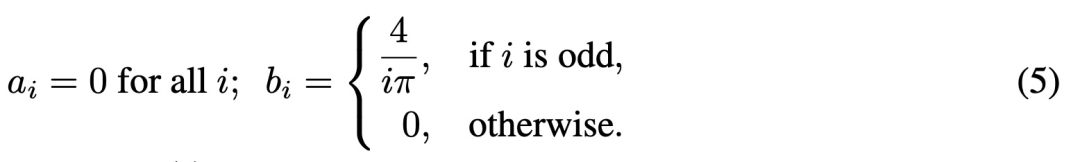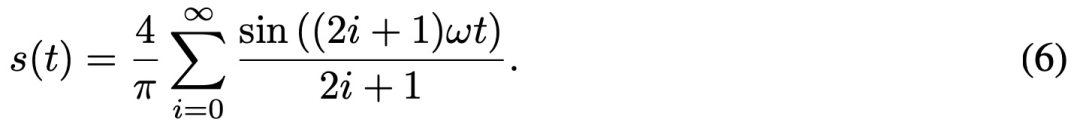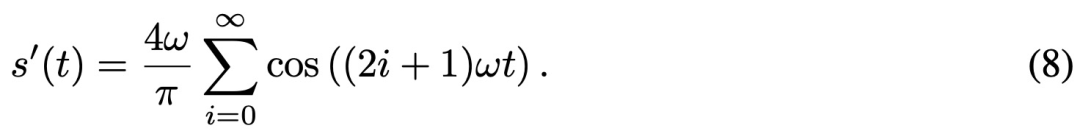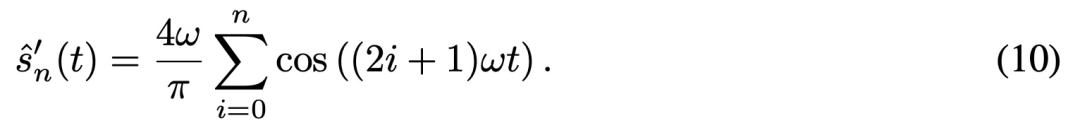常规符号函数的梯度几乎处处为零,不能用于反向传播。为此,来自华为诺亚方舟实验室等机构的研究者提出一种在频域中估计原始符号函数梯度的新方法。
二值神经网络(BNN)将原始全精度权重和激活用符号函数表征成 1-bit。但是由于常规符号函数的梯度几乎处处为零,不能用于反向传播,因此一些研究已经提出尝试使用近似梯度来减轻优化难度。然而,这些近似破坏了实际梯度的主要方向。
基于此,在一篇 NeurIPS 2021 论文中,来自华为诺亚方舟实验室等机构的研究者提出使用傅里叶级数的组合来估计频域中符号函数的梯度以训练 BNN,即频域逼近 (FDA)。所提方法不影响占整体能量大部分的原始符号函数的低频信息,并且将高频系数使用噪声拟合模块 (noise adaptation module) 进行估计以避免大量的计算开销。
![]()
论文地址:
https://arxiv.org/pdf/2103.00841.pdf
在几个基准数据集和神经架构上的实验表明,使用该方法学习的二值网络实现了 SOTA 准确率。
数日前,在机器之心 2021 NeurIPS MeetUp China 上,论文一作许奕星为参会者解读了该论文,感兴趣的读者可以查看以下视频。
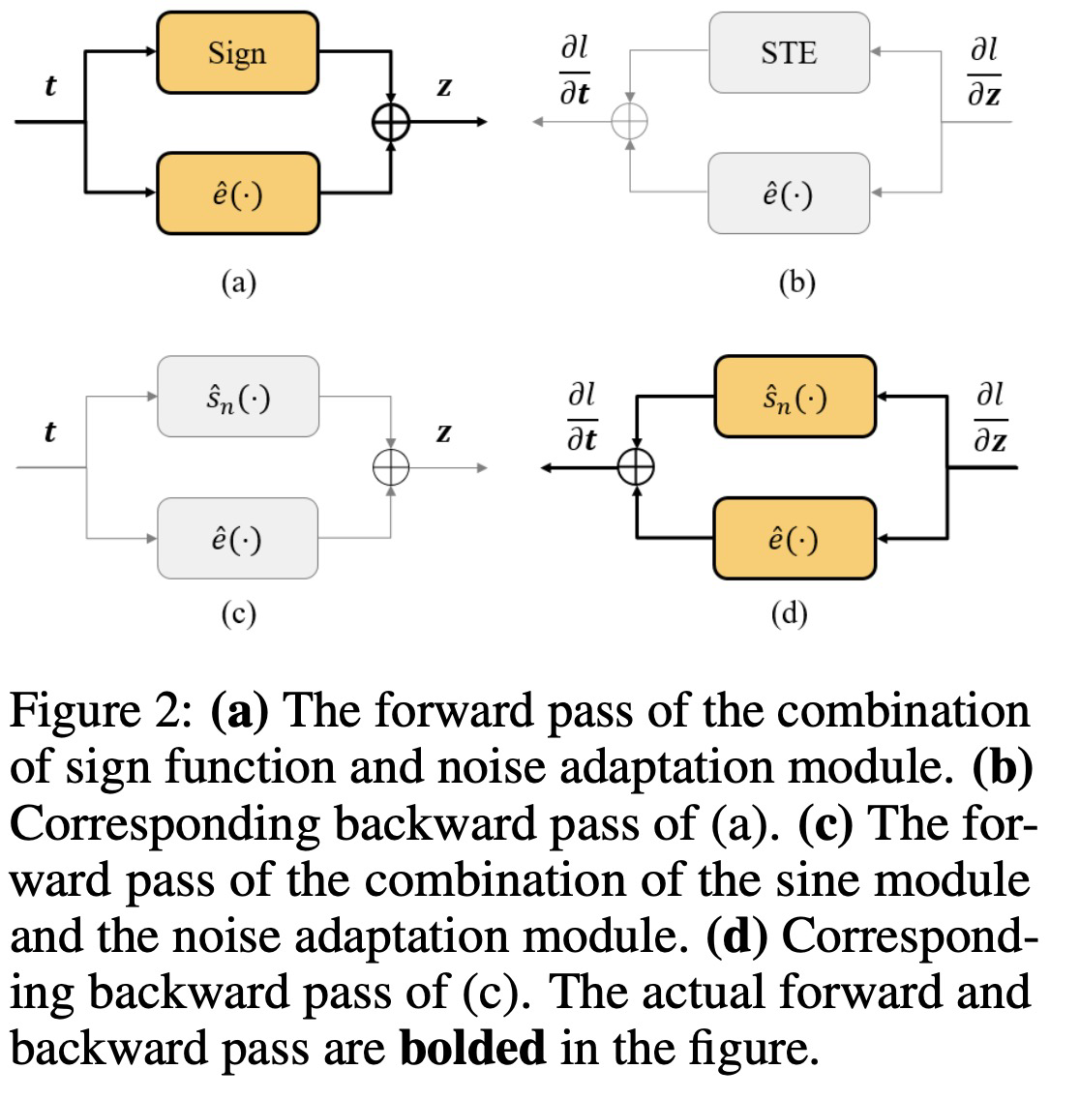
该研究提出的 FDA 方法,通过利用傅里叶级数 (FS) 来估计频域中的原始符号函数,FS 估计是使用无穷项时符号函数的无损表征。在实际应用中,能量相对较低的高频系数会被忽略,以避免巨大的计算开销,并将符号函数表征为固定数量的不同周期正弦函数的组合。与现有的逼近方法相比,该研究所提出的频域逼近方法不影响原始符号函数的低频域信息,即占用符号函数能量最多的部分。因此,原始符号函数相应梯度的主要方向能够被更准确地保持。
![]()
论文中用 f(·)和 f’(·)来表示原始函数及其对应的梯度函数。由于符号函数的梯度是一个无法反向传播的脉冲函数,需要应用进化算法(evolutionary algorithm)等零阶算法来达到最优解,但这是非常低效的。因此该研究提出找到一个代理函数,通过一阶优化算法(如 SGD)依靠实验求解,而理论上具有与符号函数相同的最优解。
已有研究证明,任何周期为 T 的周期信号都可以分解为傅里叶级数的组合:
![]()
其中 ω = 2π/T 是角频率,α_0/2 是直接分量,![]() 是正弦(余弦)分量的系数。
具体来说,当周期信号呈方波时,有:
是正弦(余弦)分量的系数。
具体来说,当周期信号呈方波时,有:
![]()
![]()
注意到当信号被限制在单个周期内时,符号函数与方波等同:
![]()
因此,符号函数也可以被分解为正弦(余弦)函数的组合,并且其导数如下:
![]()
然后,该研究提出使用上述等式 (8) 替换 STE 中的导数,以在反向传播期间更好地逼近符号函数。
当将信号从空间域转换到频域,使用无限项时,FS 分解是符号函数的无损表征,因此等式 (6) 可以重写为:
![]()
然后该研究进一步证明了随着 n 的增加,估计值![]() 和 s(t)之间的均方误差会逐渐减小,并在 n → ∞ 时收敛到 0。
为了进一步补偿细微的逼近误差,该研究在训练阶段添加了一个噪声适应模块来细化梯度。
和 s(t)之间的均方误差会逐渐减小,并在 n → ∞ 时收敛到 0。
为了进一步补偿细微的逼近误差,该研究在训练阶段添加了一个噪声适应模块来细化梯度。
![]()
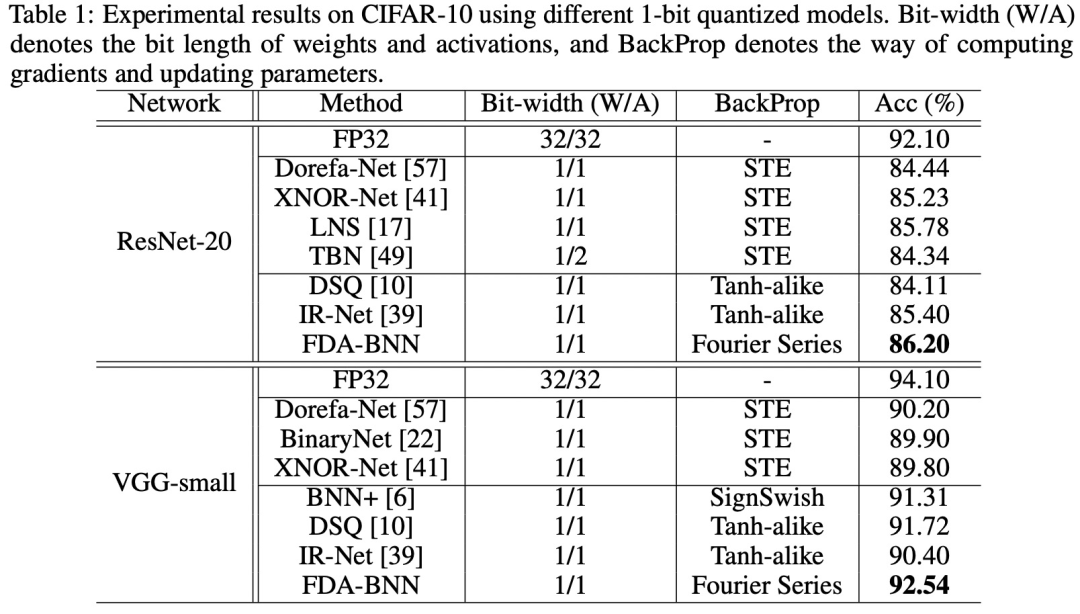
为了展示 FDA-BNN 优越的性能,该研究在 CIFAR-10 数据集上进行了评估实验,实验结果如下表所示。
![]()
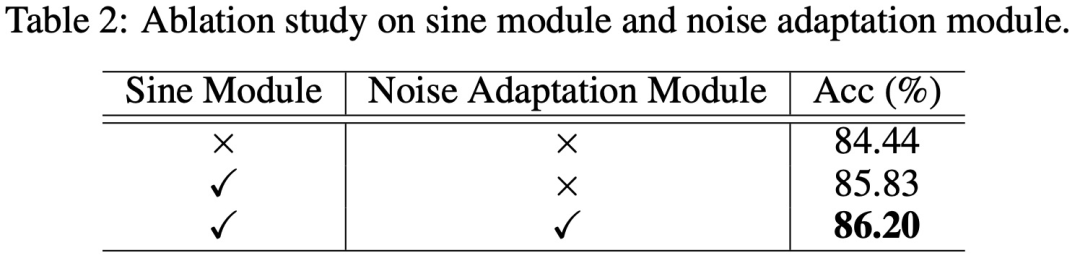
为了验证所提方法中每个组件的有效性、噪声适应模块和超参数的影响,该研究进行了一系列的消融实验。
首先,该研究使用 ResNet-20 架构在 CIFAR-10 上实验验证正弦模块和噪声适应模块的效果,结果如下表所示。
![]()
从上表的结果看,使用正弦模块可使训练过程受益,将准确率从 84.44% 提高到 85.83%。将正弦模块和噪声自适应模块组合在一起时得到了最佳性能,即 86.20% 的准确率。
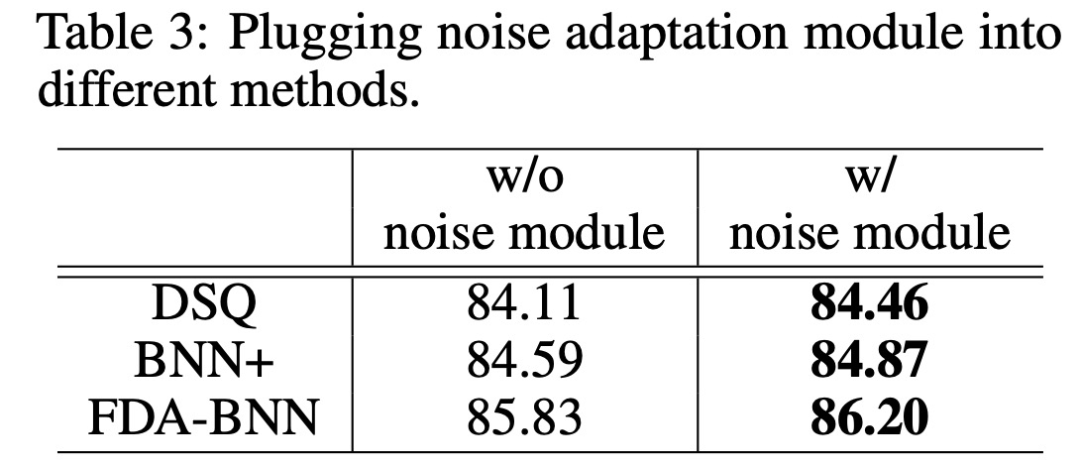
为了进一步验证噪声适应模块的用途,研究者将该模块添加到其他梯度逼近方法中,例如 DSQ 和 BNN+,结果如下表所示。
![]()
然后该研究评估了不同 η(·) 对噪声适应模块的影响。结果如下表所示,使用 shortcut 时性能更好,并且 shortcut function η(x) = α sin(x) 在实验过程中表现最好。
![]()
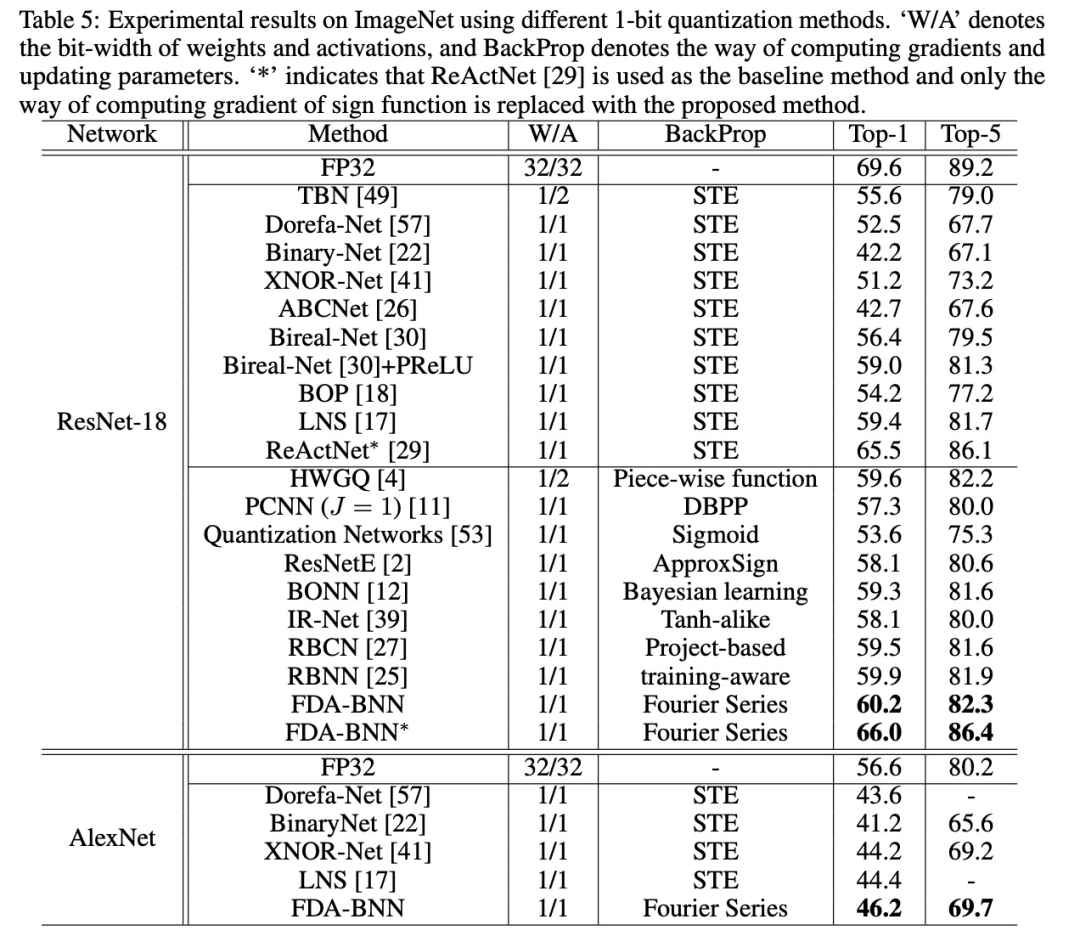
该研究进一步在大规模数据集 ImageNet ILSVRC 2012 上进行了实验,使用 ResNet-18 和 AlexNet 进行实验,结果如下表所示。
![]()
对于 ResNet-18,FDA-BNN 实现了 60.2% 的 top-1 准确率和 82.3% 的 top-5 的准确率,比基线方法(Bireal-Net + PReLU)高出 1.2% 和 1.0%,并超过所有其他方法。
当以 ReActNet 作为基线方法,并使用该研究所提方法计算符号函数的梯度, FDA-BNN 达到了 66.0% 的 top-1 准确率,86.4% 的 top-5 准确率,比基线方法分别高出 0.5% 和 0.3%。
对于 AlexNet,该研究使用 Dorefa-Net 中的量化方法作为基线方法,FDA-BNN 实现了 46.2% 的 top-1 准确率和 69.7% 的 top-5 准确率,并优于其他 SOTA 方法。
苏黎世联邦理工DS3Lab:构建以数据为中心的机器学习系统
苏黎世联邦理工学院(ETH Zurich) DS3Lab实验室由助理教授张策以及16名博士生和博士后组成,主要致力于两大研究方向,Ease.ML项目:研究如何设计、管理、加速以数据为中心的机器学习开发、运行和运维流程,ZipML项目:面向新的软硬件环境设计实现高效可扩展的机器学习系统。
12月15日-12月22日
,来自苏黎世联邦理工学院DS3Lab实验室的11位嘉宾将带来6期分享:构建以数据为中心的机器学习系统,详情如下:
![]()
© THE END
转载请联系本公众号获得授权
投稿或寻求报道:content@jiqizhixin.com
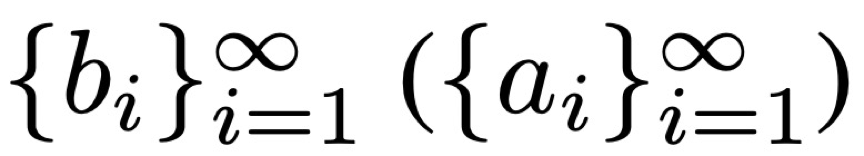 是正弦(余弦)分量的系数。
具体来说,当周期信号呈方波时,有:
是正弦(余弦)分量的系数。
具体来说,当周期信号呈方波时,有:
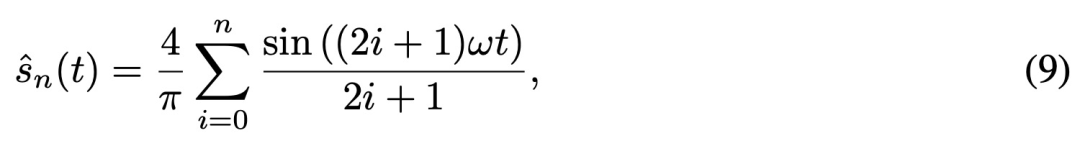
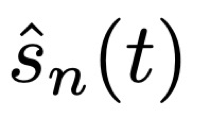 和 s(t)之间的均方误差会逐渐减小,并在 n → ∞ 时收敛到 0。
和 s(t)之间的均方误差会逐渐减小,并在 n → ∞ 时收敛到 0。