Softmax 函数和它的误解

极市导读
Softmax是个大家都熟悉的激活函数,然而,很多人只知道它的表达式,它在网络中的位置,而对一些具体的原因和细节却回答不上来。这篇文章给了相应的介绍。 >>加入极市CV技术交流群,走在计算机视觉的最前沿
Softmax 是一个数学函数,用于对 0 和 1 之间的值进行归一化。
在本文中,您将了解:
-
什么是 Softmax 激活函数及其数学表达式? -
它是如何使用 argmax() 函数实现的? -
为什么 Softmax 只用在神经网络的最后一层? -
对 Softmax 的误解
什么是 Softmax 激活函数及其数学表达式?
在深度学习中,使用 Softmax 作为激活函数,对 0 到 1 之间的向量中每个值的输出和尺度进行归一化。Softmax 用于分类任务。在网络的最后一层,会生成一个 N 维向量,分类任务中的每个类对应一个向量。
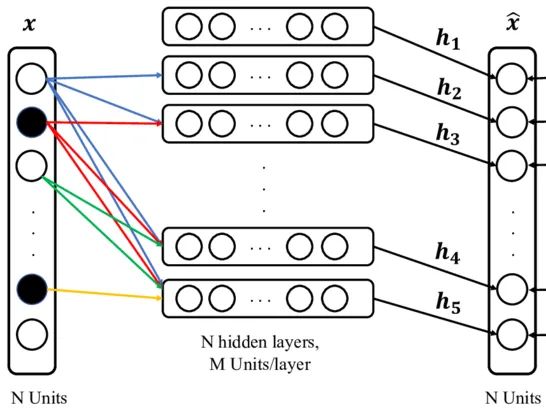
Softmax 用于对 0 和 1 之间的那些加权和值进行归一化,并且它们的和等于 1,这就是为什么大多数人认为这些值是类的概率,但这是一种误解,我们将在本文中讨论它。
实现 Softmax 函数的公式:
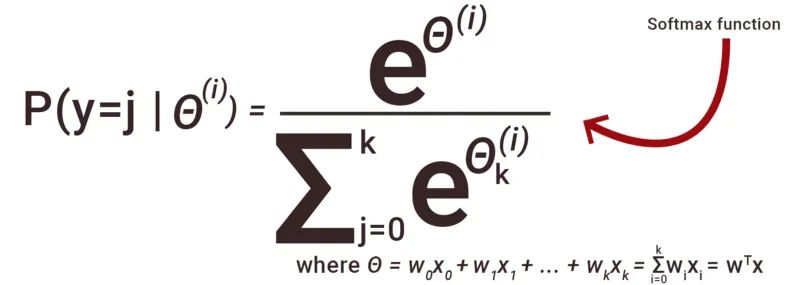
使用这个数学表达式,我们计算每类数据的归一化值。这里 θ(i) 是我们从展平层得到的输入。
计算每个类的归一化值,分子是类的指数值,分母是所有类的指数值之和。使用 Softmax 函数,我们得到 0 到 1 之间的所有值,所有值的总和变为等于 1。因此人们将其视为概率,这是他们的误解。
它如何使用 argmax() 函数?
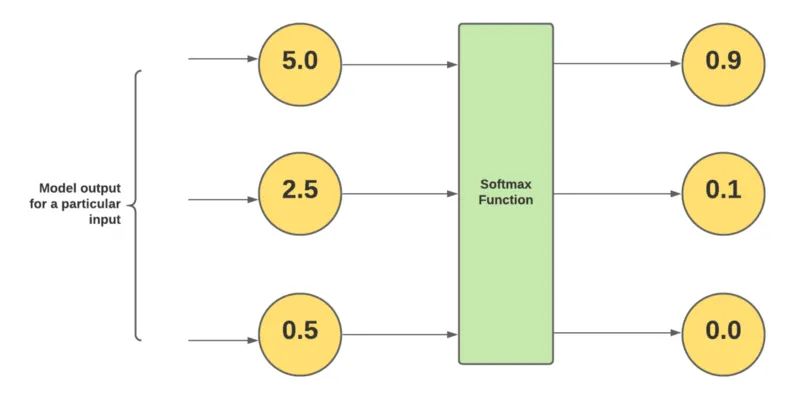
在对每个类应用上述数学函数后,Softmax 会为每个类计算一个介于 0 和 1 之间的值。
现在我们每个类都有几个值,为了分类输入属于哪个类,Softmax 使用 argmax() 给出了应用 Softmax 后具有最大值的值的索引。

为什么 Softmax 只用在神经网络的最后一层?
现在进入重要部分,Softmax 仅用于最后一层以对值进行归一化,而其他激活函数(relu、leaky relu、sigmoid 和其他各种)用于内层。
如果我们看到其他激活函数,如 relu、leaky relu 和 sigmoid,它们都使用唯一的单个值来带来非线性。他们看不到其他值是什么。
但是在 Softmax 函数中,在分母中,它取所有指数值的总和来归一化所有类的值。它考虑了范围内所有类的值,这就是我们在最后一层使用它的原因。要通过分析所有的值来知道Input属于哪个类。
对 Softmax 的误解
关于 Softmax 的第一个也是最大的误解是,它通过归一化值的输出是每个类的概率值,这完全错误。这种误解是因为这些值的总和为 1,但它们只是归一化值而不是类的概率。

在最后一层并不是单独使用 Sotmax,我们更喜欢使用 Log Softmax,它只是对来自 Softmax 函数的归一化值进行对数。
Log Softmax 在数值稳定性、更便宜的模型训练成本和 Penalizes Large error(误差越大惩罚越大)方面优于 Softmax。
这就是在神经网络中用作激活函数的 Softmax 函数。相信读完本文后你对它已经有了一个清楚的了解。
原文链接:https://medium.com/artificialis/softmax-function-and-misconception-4248917e5a1c
- END -
如果觉得有用,就请分享到朋友圈吧!
公众号后台回复“CVPR21检测”获取CVPR2021目标检测论文下载~

# CV技术社群邀请函 #

备注:姓名-学校/公司-研究方向-城市(如:小极-北大-目标检测-深圳)
即可申请加入极市目标检测/图像分割/工业检测/人脸/医学影像/3D/SLAM/自动驾驶/超分辨率/姿态估计/ReID/GAN/图像增强/OCR/视频理解等技术交流群
每月大咖直播分享、真实项目需求对接、求职内推、算法竞赛、干货资讯汇总、与 10000+来自港科大、北大、清华、中科院、CMU、腾讯、百度等名校名企视觉开发者互动交流~