【KDD2020】最小方差采样用于图神经网络的快速训练

Minimal Variance Sampling with Provable Guarantees for Fast Training of Graph Neural Networks

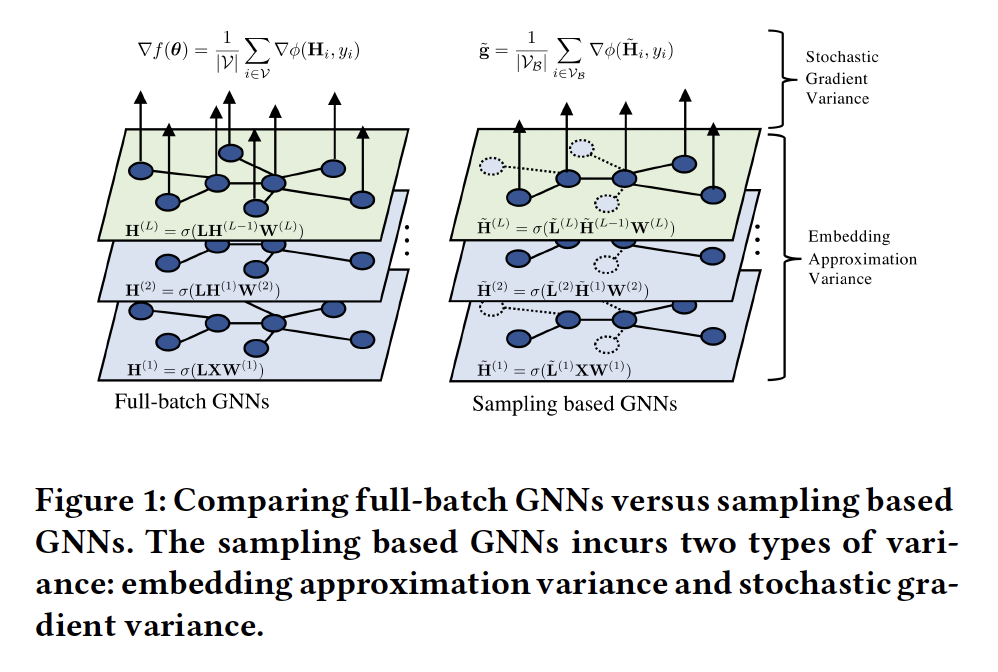
抽样方法(如节点抽样、分层抽样或子图抽样)已成为加速大规模图神经网络(GNNs)训练不可缺少的策略。然而，现有的抽样方法大多基于图的结构信息，忽略了最优化的动态性，导致随机梯度估计的方差较大。高方差问题在非常大的图中可能非常明显，它会导致收敛速度慢和泛化能力差。本文从理论上分析了抽样方法的方差，指出由于经验风险的复合结构，任何抽样方法的方差都可以分解为前向阶段的嵌入近似方差和后向阶段的随机梯度方差，这两种方差都必须减小，才能获得较快的收敛速度。本文提出了一种解耦的方差减小策略，利用(近似)梯度信息自适应地对方差最小的节点进行采样，并显式地减小了嵌入近似引入的方差。理论和实验表明，与现有方法相比，该方法即使在小批量情况下也具有更快的收敛速度和更好的泛化能力。