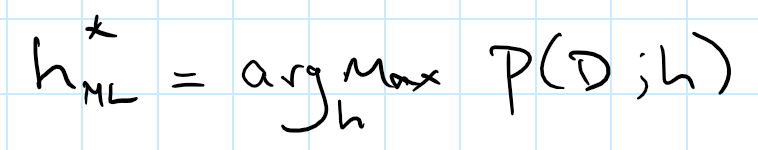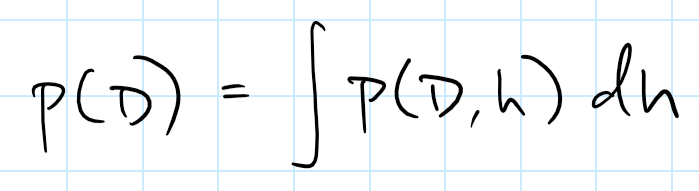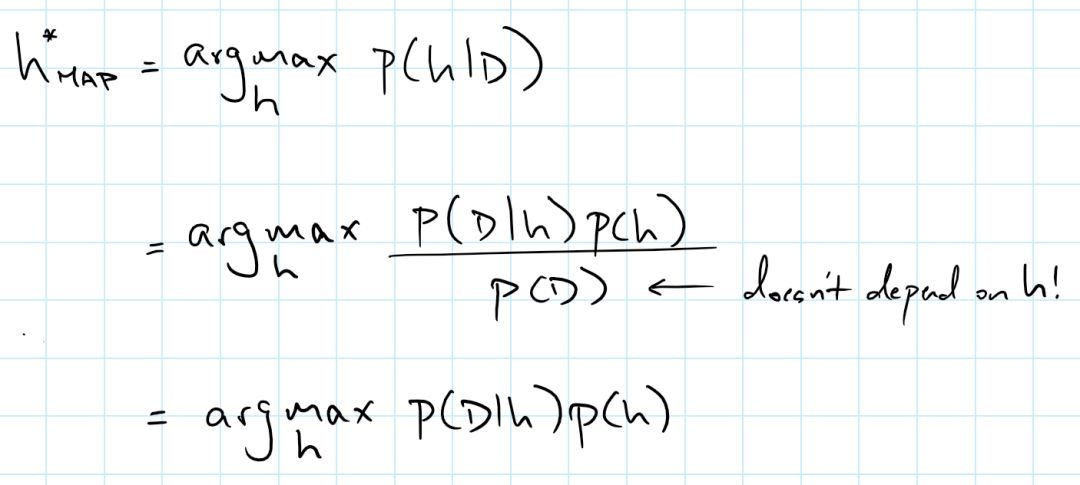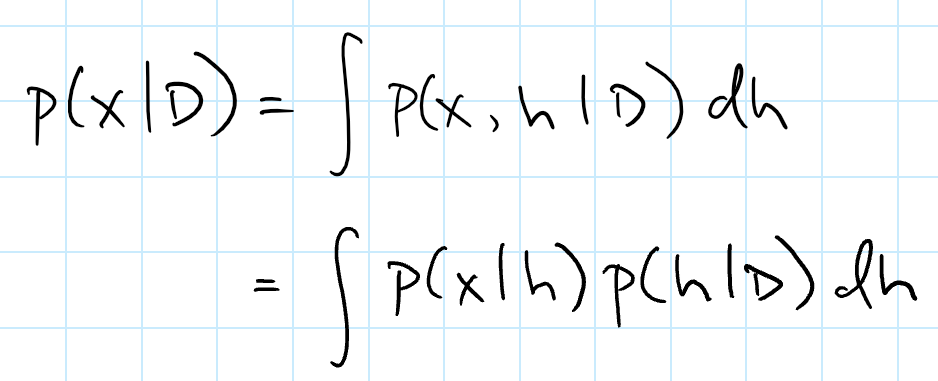什么是最大似然估计、最大后验估计以及贝叶斯参数估计

假如你有一个硬币。你把它投掷 3 次，出现了 3 次正面。下一次投掷硬币正面朝上的概率是多少? 这是一个从数据中估计参数的基础机器学习问题。在这种情况下，我们要从数据 D 中估算出正面朝上 h 的概率。

最大似然估计

一种方法是找到能最大化观测数据的似然函数（即 P(D;h)）的参数 h 的值。在这里，我们用「；」来表示 h 是一个关于概率分布 P 的参数，意味着参数 h 定义了分布 P，但是分布 P 只是说明了观测数据 D 成立的可能性有多大。

这是被称为「最大似然估计」的最常用的参数估计方法。通过该方法，我们估计出 h=1.0。

但是直觉告诉我们，这是不可能的。对于大多数的硬币来说，还是存在反面朝上的结果的可能性，因此我们通常希望得到像 h=0.5 这样的结果。

先验和后验

如何将这种直觉数学化地表述出来呢？我们可以定义一个观测数据和参数的联合概率：p(D, h) = p(D|h)p(h)。我们定义一个先验分布 p（h) 来表示在观测前关于 h 应该是什么值的直觉，以及在给定参数 h 的情况下的条件概率 p(D|h)。

如何利用现有的数据 D 估计参数 h 呢？我们需要得到后验分布 p（h|D），但是目前只有分布 P(D|h) 和 p(h)。这时候，你需要贝叶斯公式来帮忙!

贝叶斯公式：P(h|D)=P(D|h)*P(h)/P(D)

但是，这里的分母是一个问题：

一般来说，计算这个积分是不可能的。对于这个投硬币的例子来说，如果使用非常特殊的共轭先验分布，就可以绕过这个问题。

最大后验估计

但实际上，我们可以抛开归一化常数 P(D) 以更巧妙的方式讨论 p(h|D)。也就是说归一化常数不改变分布的相对大小，我们可以在不做积分的情况下找到模式：

这就是人们所熟知的最大后验估计（MAP）。有很多种方法可以算出变量 h 的确切值，例如：使用共轭梯度下降法。

贝叶斯参数估计

有了最大后验估计，可以通过先验分布来引入我们的直觉，并且忽略归一化积分，从而得到后验分布模式下的关于 h 的点估计。

但是如果我们试着用近似方法求积分呢？如果按通常的独立同分布假设，我们可以利用这个事实：未来可能出现的数据样本值 x 条件独立于给定参数 h 时的观测值 D。

这并非使用与后验概率 p(h|D) 模式相应的参数 h 的单一值来计算 P(x|h)，而是一个更加「严格」的方法，它让我们考虑到所有可能的 h 的后验值。这种方法被称为贝叶斯参数估计。

注意，存在两个关于概率分布的重要任务：

• 推断：给定已知参数的联合分布，通过其它变量的边缘概率和条件概率估计一个变量子集上的概率分布。

• 参数估计：从数据中估计某个概率分布的未知参数

贝叶斯参数估计将这两项任务构造成了「同一枚硬币的两面」：

估计在一组变量上定义的概率分布的参数，就是推断一个由原始变量和参数构成的元分布。

当然，实际上要做到这一点，需要计算困难的积分，我们将不得不用类似于「马尔可夫链蒙特卡洛算法」或者变分推断等方法取近似。 

原文链接：

https://medium.com/@amatsukawa/maximum-likelihood-maximum-a-priori-and-bayesian-parameter-estimation-d99a23a0519f

媒体合作请联系：

邮箱：contact@dataunion.org