部分特征值统计量的中心极限定理及其应用

项目名称： 部分特征值统计量的中心极限定理及其应用

项目编号： No.11471140

项目类型： 面上项目

立项/批准年度： 2015

项目学科： 数理科学和化学

项目作者： 姜丹丹

作者单位： 吉林大学

项目金额： 75万元

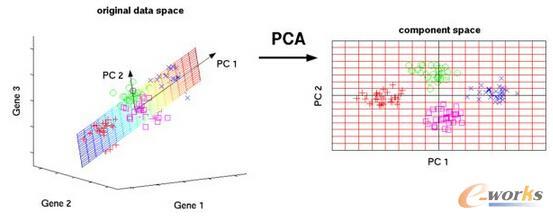
中文摘要： 在大数据时代，由于数据爆炸式的增长，经典数理统计中的理论结果和统计方法不再适用，急需一套有力的理论工具来处理大维数据的统计分析问题。大维随机矩阵谱理论的发展为解决相关问题提供了理论支持，并被广泛应用于信息、金融、医学、生物、心理学以及政府服务等各个领域。但是，关于大维主成分分析和因子分析的检验的问题，还鲜有文章涉及，而这类问题在信号处理、经济数据分析以及心理学等方面都有重要应用。因此，本项目运用大维随机矩阵谱理论，推导大维样本协方差矩阵的部分特征值的线性谱统计量的中心极限定理，并以此为理论工具提出大维总体主成分的个数的检验方法以及大维因子分析中模型拟合的检验方法，并将其应用于各领域中的实际问题，从而拓宽大维随机矩阵理论在大维数据分析中的应用范围，使之拥有更广阔的应用前景。

中文关键词： 大维随机矩阵谱理论；中心极限定理；主成分分析；因子分析

英文摘要： In the era of big data, the classical theory and statistical methods of mathematical statistics are no longer applicable for the large dimensional data, due to the explosive growth of data. It is necessary to develop a powerful theoretical tool to deal with the statistical analysis of large dimensional data. The development of spectral theory of large dimensional random matrices makes it possible to solve the above issues. It is widely applied in various fields such as information, finance, medicine, biology, psychology and government services. However, the tests in large dimensional principal component analysis and factor analysis are rarely mentioned in the articles, and such problems have important applications in signal processing, economic data analysis and psychology, etc. Therefore, this project derives CLT for Linear Spectral Statistics of a part of eigenvalues of large dimensional sample covariance matrix by using the spectral theory of large dimensional random matrices. Based on this, the new methods for the tests of large dimensional principal component analysis and factor analysis are provided, and applied into practical problems in various fields, thus broadening the scope of application of large dimensional random matrix theory in the large dimensional data analysis.

英文关键词： Spectral Theory of Large Dimensional Random Matrices;Central Limit Theorem;Principal Components Analysis;Factor Analysis