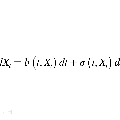多维延迟系统数值方法的延迟依赖稳定性

项目名称： 多维延迟系统数值方法的延迟依赖稳定性

项目编号： No.10971077

项目类型： 面上项目

立项/批准年度： 2010

项目学科： 数理科学和化学

项目作者： 黄乘明

作者单位： 华中科技大学

项目金额： 26万元

中文摘要： 延迟微分方程数值方法的延迟依赖稳定性能提供数值方法的完整稳定特性。但由于理论分析的困难性，该研究迄今局限于常系数线性标量模型方程。本项目致力于多维延迟系统数值方法的延迟依赖稳定性分析。我们将对线性问题和非线性问题分别展开研究，分析配置方法、线性多步方法、单支方法等多类重要算法的延迟依赖稳定性。同时，还将对随机延迟系统引入该类研究，调查Euler-Maruyama方法、随机Theta方法等常用算法的延迟依赖稳定性。本项目将为多维延迟系统和随机延迟系统数值方法稳定性分析建立新的有效研究途径，从实质上推动该领域研究向纵深发展。所获成果理论上将进一步丰富和发展延迟微分方程数值和解析稳定性理论，实践上将在自动控制、航空航天、计算生物等工程领域具有广泛应用前景。

中文关键词： 延迟微分方程；数值方法；延迟依赖稳定性；非线性稳定性；随机微分方程

英文摘要：

英文关键词： Delay differential equations；numerical methods；delay-dependent stability；nonlinear stability；stochastic differential Eqs.