BERT可以上几年级了？Seq2Seq“硬刚”小学数学应用题

会员服务 ·

BERT可以上几年级了？Seq2Seq“硬刚”小学数学应用题

2020 年 10 月 26 日 PaperWeekly

©PaperWeekly 原创 · 作者｜苏剑林

单位｜追一科技

研究方向｜NLP、神经网络

“盈亏问题”、“年龄问题”、“植树问题”、“牛吃草问题”、“利润问题”...，小学阶段你是否曾被各种花样的数学应用题折磨过呢？没关系，现在机器学习模型也可以帮助我们去解答应用题了，来看看它可以上几年级了？

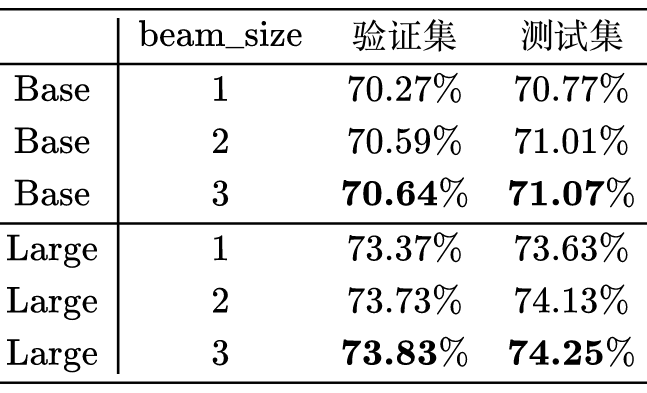
本文将给出一个求解小学数学应用题（Math Word Problem）的 baseline，基于ape210k 数据集 [1] 训练，直接用 Seq2Seq 模型生成可执行的数学表达式，最终 Large 版本的模型能达到 73%+ 的准确率，高于 ape210k 论文所报告的结果。

所谓“硬刚”，指的是没有对表达式做特别的转换，也没有通过模板处理，就直接生成跟人类做法相近的可读表达式。

数据处理

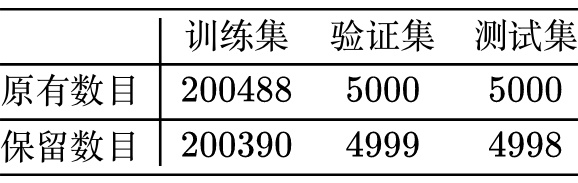
这里我们先观察一下 ape210k 数据集的情况：

{
    "id": "254761",
    "segmented_text": "小 王 要 将 150 千 克 含 药 量 20% 的 农 药 稀 释 成 含 药 量 5% 的 药 水 ． 需 要 加 水 多 少 千 克 ？",
    "original_text": "小王要将150千克含药量20%的农药稀释成含药量5%的药水．需要加水多少千克？",
    "ans": "450",
    "equation": "x=150*20%/5%-150"
}

{
    "id": "325488",
    "segmented_text": "一 个 圆 形 花 坛 的 半 径 是 4 米 ， 现 在 要 扩 建 花 坛 ， 将 半 径 增 加 1 米 ， 这 时 花 坛 的 占 地 面 积 增 加 了 多 少 米 * * 2 ．",
    "original_text": "一个圆形花坛的半径是4米，现在要扩建花坛，将半径增加1米，这时花坛的占地面积增加了多少米**2．",
    "ans": "28.26",
    "equation": "x=(3.14*(4+1)**2)-(3.14*4**2)"
}

可以看到，我们主要关心的是 original_text、equation、ans 字段，其中 original_text 就是题目，equation 则是运算过程（一般以 x= 开头），而 ans 是最终答案。我们希望训练一个模型，由 original_text 来生成 equation，然后经由 python 的 eval 函数直接得到 ans。

不过，我们需要做一些前处理，因为 ape210k 给出的 equation 并不是都可以直接 eval 的，像上面的例子 150*20%/5%-150 对 python 来说就是一个非法表达式。笔者所做的处理如下：

对于a%这样的百分数，统一替换为(a/100)；
对于a(b/c)这样的带分数，统一替换为(a+b/c)；
对于(a/b)这样的真分数，在题目中去掉括号变为a/b；
对于比例的冒号:，统一替换为/。

经过这样处理后，大部分 equation 都可以直接 eval 了，并且可以与ans进行答案对比，只保留结果一致的题目。

不过，还有一点改进的地方，就是这样得到的表达式可能会带有一些冗余的括号（也就是去掉括号后与原来的等价），因此还要加上一步去括号，即遍历每一组括号，如果去掉该组括号结果与原来的等价，那么就去掉该组括号，这样可以得到平均长度更短的表达式，而长度越短越容易生成。

最终，我们得到了如下可用的数据集：

剩下的基本上是一些错题、乱题了，暂时忽略。

模型简介

模型其实是最没什么好讲的，就是以 original_text 为输入、equation 为输出，以“BERT+UniLM”为基础架构，训练一个 Seq2Seq 模型。如果对模型还有什么疑惑的地方，请阅读从语言模型到Seq2Seq：Transformer如戏，全靠Mask。

项目链接：

http://github.com/bojone/ape210k_baseline

笔者的训练是用 22G 的单卡 TITAN RTX 跑的，优化器是 Adam，学习率是 2e-5。Base 版本的用了 batch_size=32，大概需要训练 25 个 epoch，每个 epoch 约 50 分钟（算上验证集的评测时间）；而 large 版本则是 batch_size=16，大概需要训练 15 个 epoch，每个 epoch 约 2 小时（算上验证集的评测时间）。

对了，说到 Large，由于 UniLM 借用了 MLM 部分权重，所以我们不能用哈工大开源的 RoBERTa-wwm-ext-large [2] ，因为这个版本的 MLM 权重是随机初始化的（但它的 Base 版本是正常的，可以用）。Large 版本推荐用腾讯 UER [3] 开源的权重，原本是 PyTorch 版的，笔者将它转换为 TF 版了，可以通过下方链接下载。

网盘链接：

https://pan.baidu.com/s/1Xp_ttsxwLMFDiTPqmRABhg

提取码： l0k6

效果如下表：

Large 模型的结果已经比 ape210k 的论文 Ape210K: A Large-Scale and Template-Rich Dataset of Math Word Problems [4] 所报告的 70.20% 要明显高了，因此说明我们这里的模型是一个不算太差的 baseline。

感觉如果用一些 Seq2Seq 的技巧来缓解一下 Exposure Bias 问题（参考Seq2Seq中Exposure Bias现象的浅析与对策），模型还能有进一步提升；还有或许可以引入 copy 机制，增强输出与输入数字的一致性；还有可以想办法进一步缩短序列长度（比如四个字符的 3.14 替换为两个字母 pi）。这些就留给大家尝试了。

标准输出

如果纯粹从建模的角度来看，其实我们的任务已经完成了，即模型只需要输出式子就行了，评测的时候则只需要判断式子 eval 后的结果跟参考答案是否一致就好。

但是从实际实用的角度，我们还需要对输出做进一步的标准化，即根据不同的题目决定输出的是小数、整数、分数还是百分数等，这就需要我们：1）决定什么时候该输出什么格式；2）根据指定格式对结果进行转换。

第一步比较简单，一般来说根据题目或方程的一些关键字就可以判断了。比如表达式里边如果有小数的，那么输出结果一般也是小数；如果题目是问“多少辆”、“多少个”、“多少人”之类的，那么输出的都是整数；如果直接问“几分之几”或“百分之几”的，那么相应地就是分数或百分数了。

比较困难是应该是取整类题目，比如“每盒蛋糕 7.90 元，50 元最多可以买多少盒蛋糕?”要求我们对 50/7.90 进行下取整，但有时候则是上取整。不过让笔者很意外的是，ape210k 里边并没有取整类题目，所以也就不存在这个问题。如果遇到有取整的数据集，如果规则判断起来比较困难，那么最直接的方法就是把取整符号也加入到 equation 中让模型去预测。

第二步看起来有点复杂，主要是分数的场景，一般读者可能不知道如何让式子保留分数运算结果，如果直接 eval('(1+2)/4')，那么得到的是 0.75（Python3），但有时我们希望得到的是分数结果 3/4。

事实上，保持分数的运算属于 CAS 的范畴（Computer Algebra System，计算机代数系统），说白了就是符号运算而不是数值运算，而 Python 中刚好也有这样的工具，那就是 SymPy [5] ，利用 SymPy 就能达到我们的目的了。具体请看下面的例子：

from sympy import Integer
import re

r = (Integer(1) + Integer(2)) / Integer(4)
print(r)  # 输出是 3/4 而不是 0.75

equation = '(1+2)/4'
print(eval(equation))  # 输出是 0.75

new_equation = re.sub('(\d+)', 'Integer(\\1)', equation)
print(new_equation)  # 输出是 (Integer(1)+Integer(2))/Integer(4)
print(eval(new_equation))  # 输出是 3/4