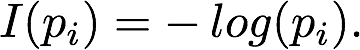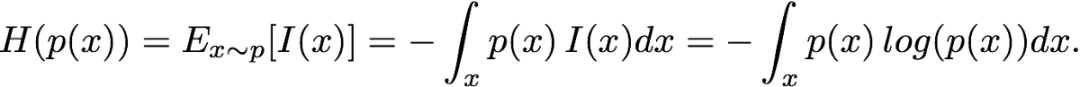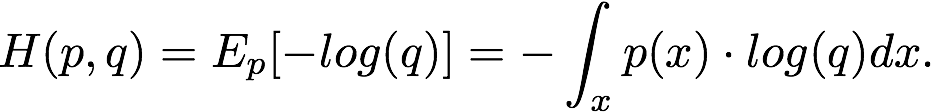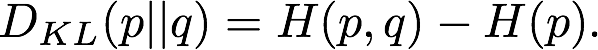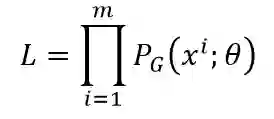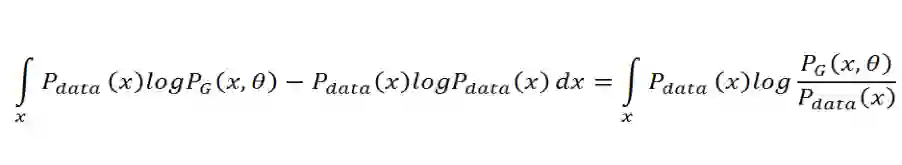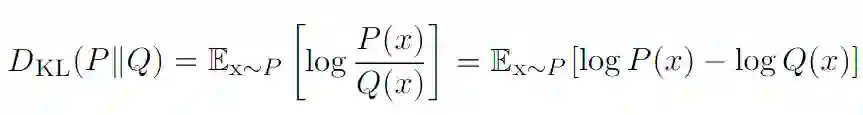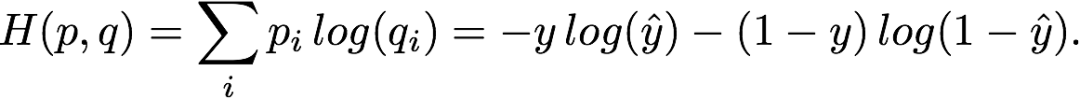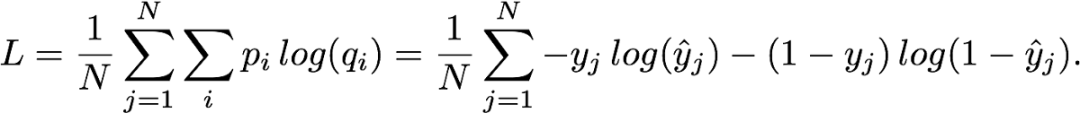从香农熵到手推KL散度：一文带你纵览机器学习中的信息论

2018 年 1 月 14 日 算法与数学之美 Frank Preiswerk

信息论与信息熵是 AI 或机器学习中非常重要的概念，我们经常需要使用它的关键思想来描述概率分布或者量化概率分布之间的相似性。在本文中，我们从最基本的自信息和信息熵到交叉熵讨论了信息论的基础，再由最大似然估计推导出 KL 散度而加强我们对量化分布间相似性的理解。最后我们简要讨论了信息熵在机器学习中的应用，包括通过互信息选择决策树的特征、通过交叉熵衡量分类问题的损失和贝叶斯学习等。

>>>>

信息论是应用数学的一个分支，主要研究的是对一个信号包含信息的多少进行量化。它最初被发明是用来研究在一个含有噪声的信道上用离散的字母表来发送消息，例如通过无线电传输来通信。而本文主要探讨信息熵在 AI 或机器学习中的应用，一般在机器学习中，我们可以将信息论应用在连续型变量上，并使用信息论的一些关键思想来描述概率分布或者量化概率分布之间的相似性。

因此在机器学习中，通常要把与随机事件相关信息的期望值进行量化，此外还要量化不同概率分布之间的相似性。在这两种情况下，香农熵都被用来衡量概率分布中的信息内容。香农熵是以信息论之父 Claude Shannon 的名字命名的，也称为信息熵或微分熵（连续）。

自信息

香农熵的基本概念就是所谓的一个事件背后的自信息（self-information），有时候也叫做不确定性。自信息的直觉解释如下，当某个事件（随机变量）的一个不可能的结果出现时，我们就认为它提供了大量的信息。相反地，当观察到一个经常出现的结果时，我们就认为它具有或提供少量的信息。将自信息与一个事件的意外性联系起来是很有帮助的。例如，一个极其偏畸的硬币，每一次抛掷总是正面朝上。任何一次硬币抛掷的结果都是可以完全预测的，这样的话我们就永远不会对某次结果感到惊奇，也就意味着我们从这个实验中得到的信息是 0。换言之，它的自信息是 0。如果硬币的偏畸程度稍微小一些，这样的话，尽管看到正面朝上的概率超过了 50%，每次抛掷还会有一些信息。因此，它的自信息大于 0。如果硬币的偏畸程度是导致反面朝上的结果，我们得到的自信息还是 0。在使用一个没有偏畸的硬币做实验时，每次抛掷得到正面朝上和反面朝上的概率都是 50%，我们会得到最大的意外性，因为在这种情况下硬币抛掷的结果的可预测性是最小的。我们也可以说，均匀分布的熵最大，确定事件的熵最小。

基于以上的非正式需求，我们可以找到一个合适的函数来描述自信息。对于一个可能取值为 x_1,x_2,...,x_n 的离散随机变量 X，它的概率质量函数 P（X），以及任何正的取值在 0 到 1 之间的单调递减函数 I(p_i) 都可以作为信息的度量。此外，还有另外一个关键的属性就是独立事件的可加性；两次连续硬币抛掷的信息应该是一次单独抛掷的 2 倍。这对独立变量而言是有意义的，因为在这种情况下意外性或者不可预测性会增大为之前的两倍。形式上，对于独立事件 x_i 和 x_j 而言，我们需要 I(p_i * p_j) = I(p_i) + I(p_j)。满足所有这些要求的函数就是负对数，因此我们可以使用负对数表示自信息：

图 1 所示是自信息 I(p)。

图 1：函数 I(p) 的自信息。小概率对应着较高的自信息，反之亦然。

我们继续回到简单的硬币抛掷实验中。在信息论中，1bit（也叫做 Shannon）信息代表一次单独硬币抛掷的两种可能结果。相似地，对于两次连续抛掷而言，就需要 4 bit 来描述 4 中可能的结果。通常，用 log_2(n)（2 的对数）bit 来描述 n 个连续的独立随机事件的结果，或者是自信息。下面我们来验证一下一次连续三次的实验中自信息的计算：总共有 2^3=8 种可能的结果，每种结果的概率都是 0.5^3=0.125。所以，这次实验的自信息就是 I（0.125）= -log_2(0.125) = 3。我们需要 3bit 来描述这些所有可能的结果，那么，任何一次连续三次的硬币抛掷的自信息等于 3.0。

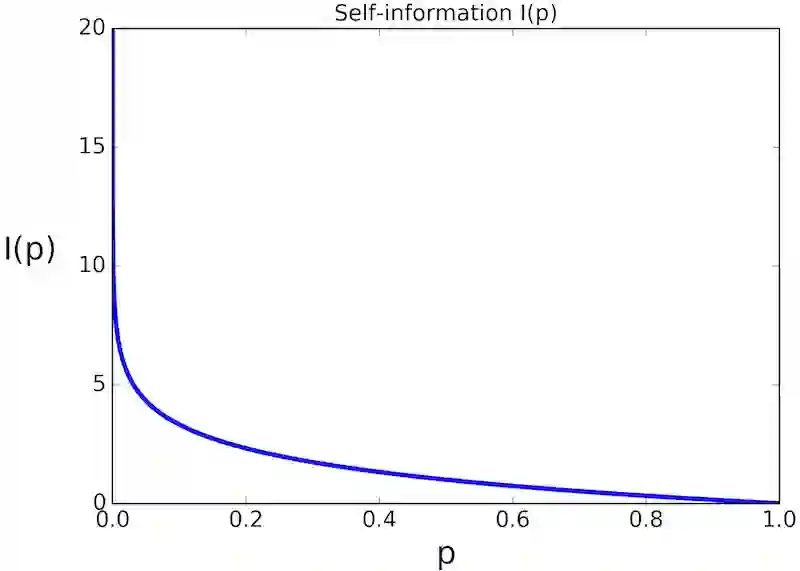
我们也可以计算连续随机变量的自信息。图 2 展示了三种不同的概率密度函数及其对应的信息函数。图 2（A）所示的 Dirac delta 对应着很强的偏差，总是同一面朝上的偏畸硬币对应着零熵。所有 p(x)= 0 的地方都对应着无限高的信息量。然而，由于这些零概率的事件永远不会发生，所以这只是一个假设。图 2（B）中的高斯概率密度函数就是对那种经常同一面朝上，但不总是同一面朝上的情况的模拟。最后，图 2（C）描述的是一个均匀分布概率密度函数，它对应着均匀的信息量，和我们没有偏畸的硬币是类似的。

图 2. [-3,3] 上的三种不同的概率密度函数及其自信息 I（p）。(A)Dirac δ函数（完全确定）；（B）μ = 0,σ = 0.5 的高斯分布；（C）均匀分布

熵

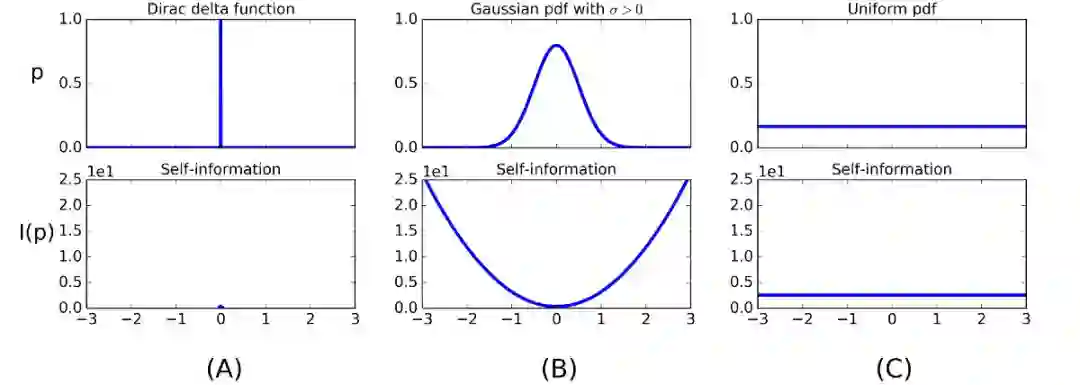
到目前为止我们只讨论了自信息。在正常的硬币实验中，自信息实际上都等于香农熵，因为所有的结果都是等概率出现的。通常，香农熵是 X 的所有可能结果的自信息期望值：

其中 b 是对数的底数。上面我们使用的是 b=2，其他常见的选择还有 b=10，以及 e。其实这个影响不大，因为不同底数的对数之间存在一个常数的关系。我们这里仍然假设底数为 2，所以我们将省略下面公式中的 b。

如果仔细注意的话，你可能会疑惑，当 p(x_i) = 0 的时候会发生什么，因为这种情况下我们必须计算 0 · log(0)。事实上，我们需要计算的是一个极限：lim_(p→0) p*log(p(x_i))=0。使用洛必达法则或泰勒展开式求解的过程读者可以查阅书籍自行完成。

当香农熵泛化到连续域的时候，通常它指的是一种微分熵，对于连续的随机变量 x 及其概率密度函数 p(x)，它的香农熵定义如下：

我们上述三个分布的熵分别是 0（狄拉克δ分布），174（高斯分布）以及 431（均匀分布）。在我们的实验中出现的模式是：越宽广的分布对应着越高的信息熵。仔细观察图 2（B）和图 2（C）有助于你的理解。尽管高斯分布中 I（p）曲线下面的面积要远大于均匀分布，然而它的信息熵要远小于均匀分布，因为信息熵 I（P）是按照概率密度 p 加权的，在高斯分布的两侧，p 接近于 0。更广的概率密度对应着更大的信息熵，有一个很好的比喻帮助记住这个：想象某种气体充满了一个储罐。从物理学中我们可以知道，一个封闭系统中的熵会随着时间增加，而且从来不会减少。在我们从储罐的另一侧注入气体之后，气体粒子的分布会收敛于一个均匀值。低熵意味着高密度的气体粒子聚集在某个特定的区域，而这是永远不会自发发生的。很多气体粒子聚集在某个小面积区域对应的还早呢故事我们的高斯概率密度函数，在狄拉克δ分布中是一个极端粒例子，所有的气体都被压缩在一个无限小的区域。

交叉熵

交叉熵是一个用来比较两个概率分布 p 和 q 的数学工具。它和熵是类似的，我们计算 log(q) 在概率 p 下的期望，而不是反过来：

在信息论中，这个量指的是：如果用「错误」的编码方式 q（而不是 p）去编码服从 q 分布的事件，我们所需要的 bit 数。在机器学习中，这是一个衡量概率分布相似性的有用工具，而且经常作为一个损失函数。因为交叉熵等于 KL 散度加上一项信息熵，即 D_KL(p||q) = H(p, q) - H(p)。而当我们针对 Q 最小化交叉熵时，H(p) 为常量，因此它能够被省略。交叉熵在这种情况下也就等价于 KL 散度，因为 KL 散度可以简单地从最大似然估计推导出来，因此下文详细地以 GAN 为例利用 MLE 推导 KL 散度的表达式。

KL 散度

与交叉熵紧密相关，KL 散度是另一个在机器学习中用来衡量相似度的量：从 q 到 p 的 KL 散度如下:D_KL(p||q)。在贝叶斯推理中，DKL(p||q) 衡量当你修改了从先验分布 q 到后验分布 p 的信念之后带来的信息增益，或者换句话说，就是用后验分布 q 来近似先验分布 p 的时候造成的信息损失。例如，在训练一个变分自编码器的隐藏空间表征时就使用了 KL 散度。KL 散度可以用熵和交叉熵表示：

交叉熵衡量的是用编码方案 q 对服从 p 的事件进行编码时所需 bit 数的平均值，而 KL 散度给出的是使用编码方案 q 而不是最优编码方案 p 时带来的额外 bit 数。从这里我们可以看到，在机器学习中，p 是固定的，交叉熵和 KL 散度之间只相差一个常数可加项，所以从优化的目标来考虑，二者是等价的。而从理论角度而言，考虑 KL 散度仍然是有意义的，KL 散度的一个属性就是，当 p 和 q 相等的时候，它的值为 0。

KL 散度有很多有用的性质，最重要的是它是非负的。KL 散度为 0 当且仅当 P 和 Q 在离散型变量的情况下是相同的分布，或者在连续型变量的情况下是『几乎处处』相同的。因为 KL 散度是非负的并且衡量的是两个分布之间的差异，它经常被用作分布之间的某种距离。然而，它并不是真的距离因为它不是对称的：对于某些 P 和 Q，D_KL(P||Q) 不等于 D_KL(Q||P)。这种非对称性意味着选择 D_KL(P||Q) 还是 D_KL(Q||P) 影响很大。

在李弘毅的讲解中，KL 散度可以从极大似然估计中推导而出。若给定一个样本数据的分布 P_data(x) 和生成的数据分布 P_G(x;θ)，那么 GAN 希望能找到一组参数θ使分布 P_g(x;θ) 和 P_data(x) 之间的距离最短，也就是找到一组生成器参数而使得生成器能生成十分逼真的图片。

现在我们可以从训练集抽取一组真实图片来训练 P_G(x;θ) 分布中的参数θ使其能逼近于真实分布。因此，现在从 P_data(x) 中抽取 m 个真实样本 {𝑥^1,𝑥^2,…,𝑥^𝑚}，其中符号「^」代表上标，即 x 中的第 i 个样本。对于每一个真实样本，我们可以计算 P_G(x^i;θ)，即在由θ确定的生成分布中，x^i 样本所出现的概率。因此，我们就可以构建似然函数：

其中「∏」代表累乘、P_G(x^i;θ) 代表第 i 个样本在生成分布出现的概率。从该似然函数可知，我们抽取的 m 个真实样本在 P_G(x;θ) 分布中全部出现的概率值可以表达为 L。又因为若 P_G(x;θ) 分布和 P_data(x) 分布相似，那么真实数据很可能就会出现在 P_G(x;θ) 分布中，因此 m 个样本都出现在 P_G(x;θ) 分布中的概率就会十分大。

下面我们就可以最大化似然函数 L 而求得离真实分布最近的生成分布（即最优的参数θ）：

在上面的推导中，我们希望最大化似然函数 L。若对似然函数取对数，那么累乘 ∏ 就能转化为累加 ∑，并且这一过程并不会改变最优化的结果。因此我们可以将极大似然估计化为求令 log[P_G(x;θ)] 期望最大化的θ，而期望 E[logP_G(x;θ)] 可以展开为在 x 上的积分形式：∫P_data(x)logP_G(x;θ)dx。又因为该最优化过程是针对θ的，所以我们添加一项不含θ的积分并不影响最优化效果，即可添加 -∫P_data(x)logP_data(x)dx。添加该积分后，我们可以合并这两个积分并构建类似 KL 散度的形式。该过程如下：

这一个积分就是 KL 散度的积分形式，因此，如果我们需要求令生成分布 P_G(x;θ) 尽可能靠近真实分布 P_data(x) 的参数θ，那么我们只需要求令 KL 散度最小的参数θ。此外，我们可以将 KL 散度的积分形式转换为我们熟悉的 KL 散度表达式：

在离散型变量的情况下，KL 散度衡量的是，当我们使用一种被设计成能够使得概率分布 Q 产生的消息的长度最小的编码，发送包含由概率分布 P 产生的符号消息时，所需要的额外信息量。

在机器学习中的使用

你或许疑问，这里的熵和机器学习是如何相关的。下面我们看一下一些具体的领域。

贝叶斯学习

首先，上面描述的高斯分布的例子是很重要的，因为在机器学习应用中，高斯分布是一个很常见的建模选择。机器学习的目标就是减少熵。我们希望做一些预测，而且我们必须对自己的预测比较确定。而熵正好可以用来衡量这个置信度。在贝叶斯学习中，经常假设一个先验分布具有较宽广的概率密度函数，这反映了随机变量在观测之前的不确定性。当数据来了以后，熵会减小，并且让后验分布在最可能的参数值周围形成峰值。

决策树学习

在决策树的学习算法中，一般包含了特征选择、决策树的生成与决策树的剪枝过程。决策树的特征选择在于选取对训练数据有分类能力的特征，而通常特征选择的准则是信息增益或信息增益比。

在李航的统计学习方法中，一般熵 H(Y) 与条件熵 H(Y|X) 之差可以称为互信息（Mutual Information），决策树学习中的信息增益等价于训练数据中类与特征的互信息。若给定训练数据集 D 和特征 A，经验熵 H(D) 表示对数据集 D 进行分类的不确定性。而经验条件熵 H(D|A) 表示在特征 A 给定的条件下对数据集 D 进行分类的不确定性。那么它们的差，即信息增益，就表示由于特征 A 而使得对数据集 D 的分类的不确定性减少的程度。显然，对于数据集 D 而言，信息增益依赖于特征，不同的特征往往具有不同的信息增益。信息增益大的特征具有更强的分类能力。

根据信息增益准则的特征选择方法是：对训练数据集（或子集）D，计算其每个特征的信息增益，并比较它们的大小，选择信息增益最大的特征。

因此在决策树学习中，熵被用来构建树。通过将数据集 S 根据可能的「最佳」属性分成一些子数据集，从根节点开始构建决策树，「最佳」属性也就是能够将得到的子数据集的熵最小化的属性。这个过程被递归地重复，直到没有更多的属性来分割。此过程被称为 ID3 算法，由此可见 ID3 算法的核心是在决策树各个结点上应用信息增益准则选择特征，递归地构建决策树。

分类

不管是在二分类问题还是多分类问题中，交叉熵是 logistic 回归和神经网络中的标准损失函数。通常，p 是真实分布，q 是模型描述的分布。让我们来看一个二分类 logistic 回归中的一个例子。两个类别的标签分别是 0 和 1，logistic 模型给每一个输入赋予以下概率：q_(y=1) =y_hat，q_(y=0) = 1- y_hat。这个可以简写为 q ∈ {y_hat, 1 − y_hat}。尽管真实标签是精确的 0 和 1，但是这里还是写成 p ∈ {y, 1 − y}，因此不要被这个表达方式搞混。在这个标记下，每个样本的真实值和估计分布之间的交叉熵如下：

当它被作为一个损失函数使用的时候，我们用的是 N 个样本的交叉熵均值，

结语

以上基本上来说就是机器学习中所涉及的信息论基础，虽然我们并不怎么使用信息论中关于消息长度的解释，但机器学习主要使用用信息论的一些关键思想来描述概率分布或者量化概率分布之间的相似性。信息论是我们构建损失函数随必须要考虑的，而且它的对数形式很容易与输出单元一般采用的指数形式相结合而提高学习的效率。此外，现代深度网络的成功与最大似然估计的流行，很大程度是因为有像信息熵那样对数形式的损失函数而取得极大的提升。

机器之心编译

参与：Nurhachu Null、蒋思源