当你增加神经网络的层数时会发生什么？

作者｜ Pradeep Mutalik

译者｜ 马卓奇

编辑｜Emily

“深度学习”是人工智能领域中的新兴词汇。Natalie Wolchover 在最近 Quanta Magazine 的文章中指出:“‘深度神经网络’已经学会了交谈、开车、通关电动游戏，并且打败了围棋冠军，做梦、画画以及帮助科学家完成科学发现。”

更多干货文章请关注微信公众号"AI 前线"，ID："ai-front"

如此巨大的成功之下，许多人们认为深度学习是一项革命性的新技术。但其实这种看法是错的。深度学习的基础可以回溯到半个多世纪之前的 AI 黎明，当时具有层连接的类神经单元的人工神经网络，和“反向传播”算法——利用误差修正来改变不同层的神经元之间的连接强度，这两项技术才刚刚创立。在过去的几十年中，这两个创新的受欢迎程度一直随时间跌宕起伏，不仅跟它们的进步和失败相关，也跟该领域的重要人物对它们的支持和蔑视相呼应。反向传播算法在 20 世纪 60 年代发明，大概同时，Frank Rosenblatt 的“感知器”学习算法引起了领域内对于人工神经网络的前景的关注。反向传播算法首先在 20 世纪 70 年代应用于这些网络，但是在受到 Marvin Minsky 和 Seymour Papert 的批判后，该领域的发展受到了打击。在 20 世纪 80 年代和 90 年代，当 David Rumelhart、Geoffrey Hinton 和 Ronald Williams 再一次将这两个想法结合起来之后，它卷土重来。但是在 21 世纪初，由于它的表现低于人们的预期，它再一次失去了关注。最终，在 2010 年左右，深度学习开始征服世界，获得了一系列前文所提到的成功。

是什么改变了？就是直接的计算能力，使得应用反向传播算法的人工神经网络可以比之前具有更多的层（这也是“深度学习”中“深度”的由来）。这一点也允许了深度学习机可以在海量数据上进行训练。同时，利用 Hinton 提出的方法，还可以允许网络进行逐层训练。

仅仅增加网络中的层数能产生这样质的差别吗？在这个月的“洞察之谜”中，让我们看看是否能利用一个简单的神经网络来证明这个想法。

问题 1

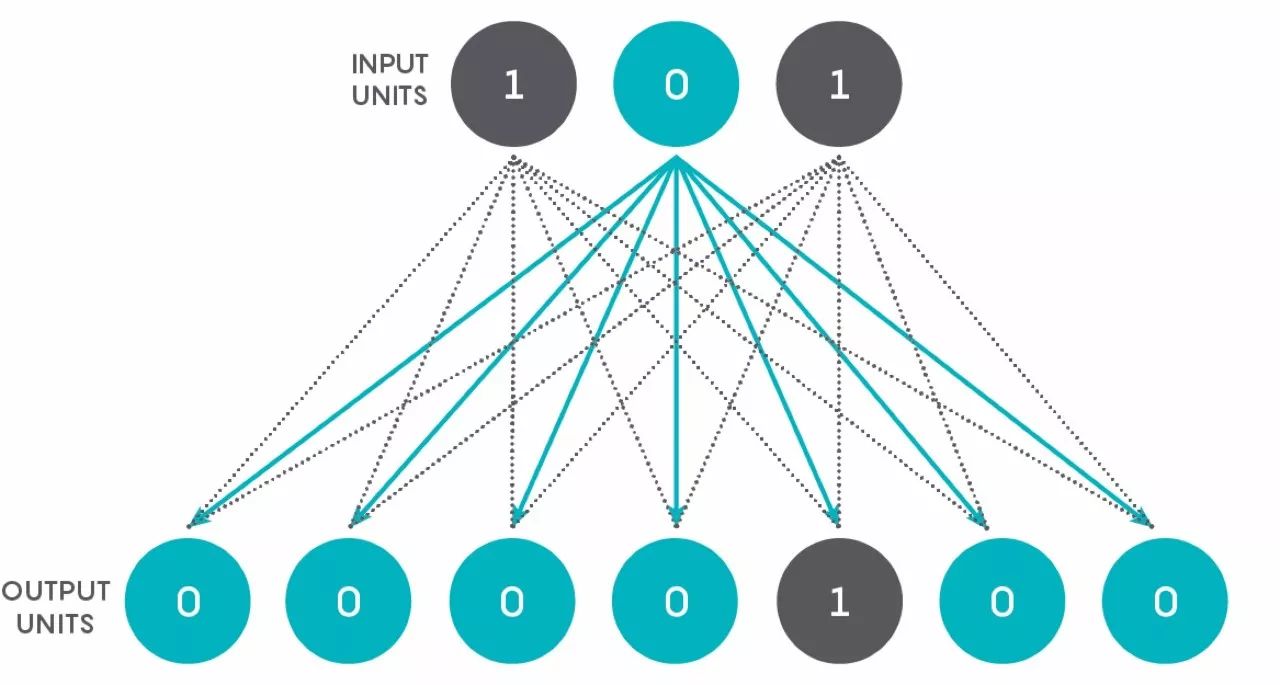
我们将要创建一个把二进制数转化为整数的简单网络。假设一个只有两层的网络——输入层由 3 个单元组成，输出层由 7 个单元组成。第一层的每个单元都与第二层的每个单元相连，如下图所示。

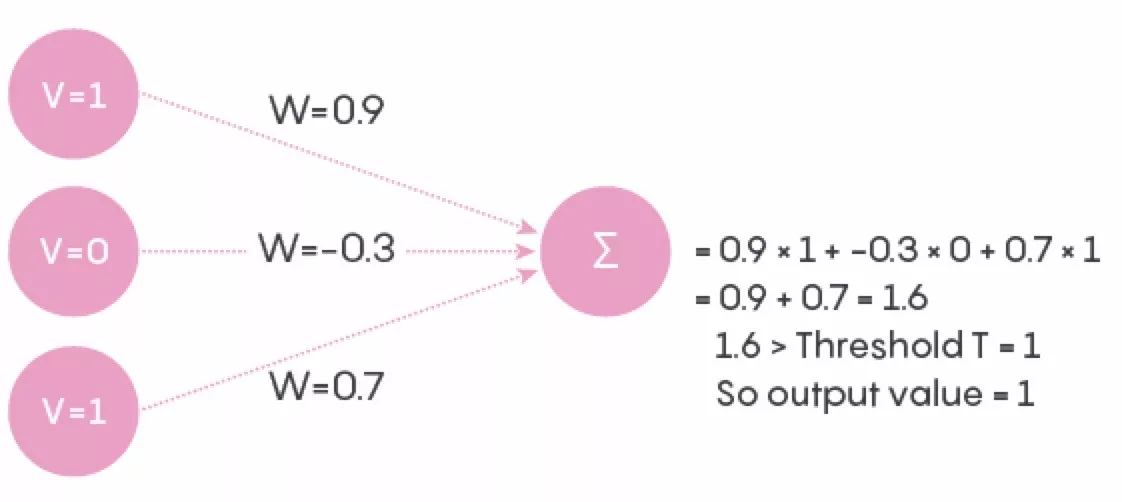
可以看到，图中一共有 21 个连接。输入层的每个单元在给定的时间点上，都处于关闭或打开的状态，其值为 0 或 1。从输入层到输出层的每个连接都有一个相关权重，在人工神经网络中，这个数字是 0 到 1 之间的实数。为了使网络更类似于一个实际的神经网络，我们将权重设置为–1 到 1 之间的实数（负号表示抑制神经元）。输入的值和连接权重的乘积传送到输出神经元，如下图所示。输出神经元将它从所有连接处得到的数字相加，获得一个单个的数字。例如下图中，使用任意的输入值和连接权重输入到单个输出神经元。基于这个数字，输出神经元决定它的状态是什么。如果数字超过一定阈值，则单元的值为 1，否则为 0。我们称值为 1 的单元为“开”或“激活”单元，值为 0 的单元为“休眠”单元。

这三个输入单元从上到下的值可以为 001，010，011，100，101，110，111，可以看作是 1-7 的二进制数。

现在问题是：是否能通过调整连接权重以及 7 个输出单元的阈值，使每个二进制数字输入仅能激活一个对应的输出单元，而其他输出单元都处于休眠？激活单元的位置反映了二进制输入所代表的值。所以，如果原始输入为 001，应该仅有最左侧的输出单元（手机用户是最底部的单元）被激活，同理，如果原始输入为 101，则应该是从左数第 5 个（手机用户则为从底部数）输出单元被激活，以此类推。

如果你觉得以上的结果不可能，那么试着调整一下权重，让结果尽量靠近。你能想到一种简单的调整方法，通过增加连接而不增加单元来改进你的答案吗？

问题 2

现在让我们引入学习方面。假设网络处在初始状态，每个连接权重为 0.5，每个输出阈值为 1。然后，网络按顺序依次输入全部 7 组输入值（重复 10 次），可以根据观测值和预期值之间的误差来调整权重和阈值。在问题 1 中，连接权重必须处在 -1 到 1 之间。你能创建一个全局的、通用的学习规则来调整连接和阈值，使问题 1 能得到或接近最优解吗？比如说，学习规则可以是“如果输出单元应该激活却处于休眠状态时，在范围内增加连接权重 0.2，减少阈值 0.1。”只要遵守特定的限制，你可以尽情创造学习规则。要注意，规则对给定层的所有单元都相同，并且必须具有通用性：它应该让网络在不同的输入和输出中都表现地更好。

问题 3

最后，让我们在输入层和输出层中间增加额外的一层，具有 5 个单元。对这个 3 层网络进行分析会需要计算机的帮助，例如使用电子表格或者简单的模拟程序。遵循上面相同的规则，并且隐藏层有额外的规则，与两层网络相比，三层网络该如何在问题 1 和 2 上执行？

这期“洞察之谜”就到这里。希望你能好好思考这个问题。希望这个练习能对你设计的神经元的连接权重和阈值进行建设性的微调！

查看英文原文：

https://www.quantamagazine.org/how-to-win-at-deep-learning-20171009/