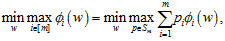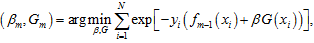Minimizing the Maximal Loss: How and Why-ICML(2)

Minimizing the Maximal Loss: How and Why

Author: Shai Shalev-Shwartz and Yonatan Wexler

前言：先说一声迟到的圣诞快乐！好啦，话不言多，立刻进入正题。这是一篇属于机器学习中计算学习理论范畴的论文，挑中这篇文章的原因是这篇文章讨论了机器学习当中的一个基础问题：如何有效最小化经验风险？我们知道，AdaBoost是一种采用了委员会机制的方法，通过组合弱学习器，最小化经验风险。而这篇文章提出了一种作用于采样训练数据上的“boosting”机制：基于在线学习方法，从训练集中每次采样有利于当前优化的样本数据，用以模型学习效率的提升。接下来，进入正题！

 1  知识点概要

---

 a  PAC（Probably Approximately Correct-可能近似正确）学习

在PAC学习理论中涉及到几个基础概念：X是输入空间，D是输入空间上的一个分布，h∈H是输入x输出标签y的一种假设（hypothesis）。PAC学习的目标是：假设训练集是来自于D的独立同分布地采样，目标是找到一种假设h，使得L_D(h)< ε，其中L_D(h)=P_x~D[h(x)≠h^*(x)]，h^*表示最优假设，ε表示误差范围。由于零误差的实现比较困难（ε=0），因此我们只能从概率上保证（以1−δ的概率）模型误差小于一个较小的值ε。

 

 b  VC维（Vapnik-Chervonenkis Dimension）

提到VC维就需要明确一个概念“shatter”：当假设空间H作用于N个输入样本时，产生的二分（dichotomies）数量等于这N个点总的组合数2^N时，就称这N个输入被H给shatter掉了。一个假设空间H的VC维是这个H最多能够shatter掉的点的数量，记为VC(H)。如果不管多少个点，H都能shatter它们，则VC(H)=无穷大。

VC提供了解释PAC学习可行的两个核心条件：1）是否经验误差和期望误差相近（训练和测试中的期望损失相近）？ 2）经验误差是否足够小？当VC维较小时，条件（1）容易满足，但条件（2）不容易满足。当VC维较大时，条件（2）容易满足，但条件（1）不容易满足。这就是所谓的欠拟合和过拟合问题。有一篇写得相当不错的博文深入的介绍了VC维了，大家可以参考[1]。

 2  动机及主要贡献

---

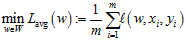
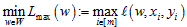
典型的有监督的机器学习应用场景为：给定训练集S=((x₁, y₁), …, (x_m,y_m))∈(X, Y)^m，学习函数h_w:X→Y，其中w∈W是函数h参数向量。定义损失函数l: W×X×Y→[0, 1]用来评价参数化的函数h在训练样本(x, y)上的表现。有两种一般的适用学习规则用来指导有监督的机器学习：1）最小化平均损失；2）最小化最大损失 。最小化L_max可以更有效地利用训练集中较为稀少的训练样本（离群点-outlier），另外，由于L_max≥L_avg，这使得在相同约束条件L_D(h)< ε下，最小化L_max能够更好地拟合训练集。但在实际应用中，最小化L_avg仍然比最小化L_max更为流行，这是因为：1）在假设训练样本独立同分布的情况下，最小化L_avg支持在线学习方法，例如：SGD（Stochastic Gradient Descent）方法；2）最小化L_max可以更好地拟合训练集，但相比最小化L_avg存在更大的过拟合风险；3）由于最小化L_max对离群点敏感，使得最小化L_max很不稳定。

那么是否可以有这样一种方法，能够综合最小化L_max以及L_avg的优势，模型在线学习的训练策略，训练过程中保证模型在有效降低经验风险的情况下，防止模型过拟合并且获得稳定的解？为此文章提出了一种在训练过程中自适应地调整训练集样本分布的方法，在线学习策略中所采样的训练集样本，其样本分布会根据当前训练的损失进行自适应地调整。这种调整策略既能保证模型能够有效捕捉训练集中的离群点信息，又能保证训练模型的稳定性，并防止因为过度拟合离群点所带来的过拟合现象。

 3   Focused Online Learning（FOL）

---

令S_m={p∈[0,1]^m: ||p||₁=1}为训练集中m个样本分布所定义的单纯形。在FOL中，损失函数的形式为：

其中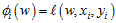。在总共T轮的训练中，在每一迭代轮t中，选取训练样本i_t ~ p_t用于当前的训练，并根据当前迭代轮的损失调整训练集中的样本分布。具体FOL算法为：

另外，作者还给出了用于快速采样训练样本以及更新样本分布的方法：

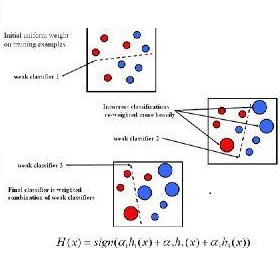
 4  FOL和AdaBoost

---

AdaBoost的策略是通过组合弱学习器的方式，最小化经验风险。假设有m个弱分类器，AdaBoost组合这m个弱分类器：

其中G_m为当前组合的弱分类器，f_m-1为m-1步的组合结果，β_m为当前弱分类器所对应的系数。在Adaboost中，系数β_m的根据第m-1步组合后的模型误差计算所得。FOL对训练样本的分布进行更新的策略近似于AdaBoost的更新策略，虽然FOL和AdaBoost的作用方式不同，但最终都能有效的最小化经验风险。

 5  实验结果

---

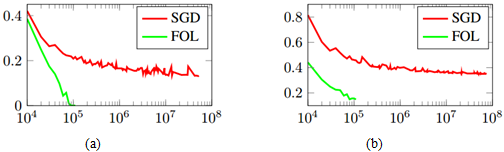
在实验中作者采用CNN模型进行人脸识别，模型分别采用了SGD和FOL这两种优化策略。在训练集上，FOL的收敛速度明显优于SGD。这是因为当分类误差达到一个很小的值（<0.4%）时，识别任务的训练对于SGD而言，每千个训练样本中只有4个训练样本是包含有效信息的。如果每个迭代步选择的batch大小为64，则SGD平均每15轮才能挑选到一个包含有效信息的训练样本。而FOL在每个迭代步平均可以包含32个有效的训练样本。在测试集上，FOL的表现性能也明显优于SGD。

图 1 FOL和SGD在训练集和测试集上随迭代步变化的误差情况。(a)训练误差；(b)测试误差。

另外，作者还与AdaBoost进行了比较，在这一点上AdaBoost的收敛速度稍优于FOL。

---

总结 这是一篇面向机器学习基础理论的文章，个人觉得文章所述对我们的实际工作也有相当的指导作用。最后提一个小问题，这个问题的答案还需要通过实际应用来进行解答：文章工作所基于的假设是线性可分的数据集，作者并没有解答如果数据中存在噪声时会对FOL方法有何种影响。这也是这篇文章的最大疑问所在。以上我并没有完全按照文章的逻辑来叙述论文，省略了相当多的理论推导，如果有感兴趣的，可以自行翻阅。最后，祝即将迎来的新年，大家元旦快乐！

 

---

参考文献：

[1]VC维的来龙去脉:

http://www.flickering.cn/machine_learning/2015/04/vc%E7%BB%B4%E7%9A%84%E6%9D%A5%E9%BE%99%E5%8E%BB%E8%84%89/