Approximability of Discriminators Implies Diversity in GANs

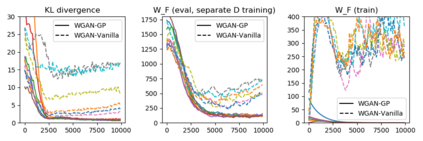
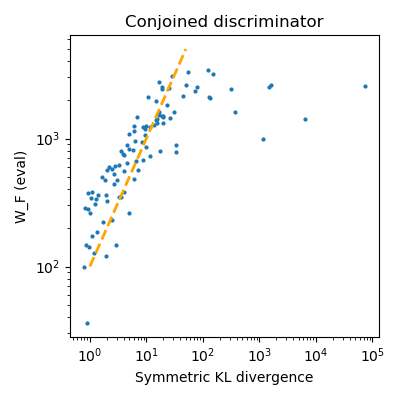
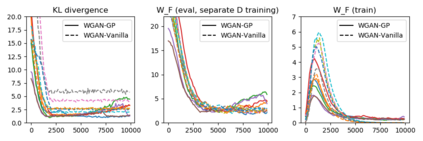
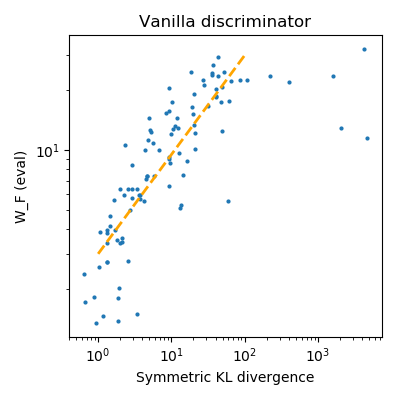
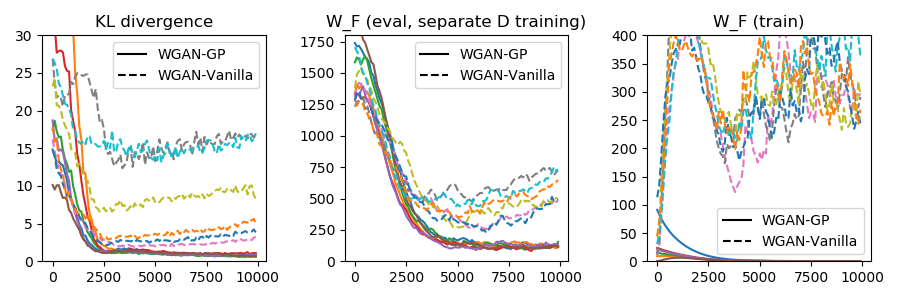
While Generative Adversarial Networks (GANs) have empirically produced impressive results on learning complex real-world distributions, recent work has shown that they suffer from lack of diversity or mode collapse. The theoretical work of Arora et al.~\cite{AroraGeLiMaZh17} suggests a dilemma about GANs' statistical properties: powerful discriminators cause overfitting, whereas weak discriminators cannot detect mode collapse. In contrast, we show in this paper that GANs can in principle learn distributions in Wasserstein distance (or KL-divergence in many cases) with polynomial sample complexity, if the discriminator class has strong distinguishing power against the particular generator class (instead of against all possible generators). For various generator classes such as mixture of Gaussians, exponential families, and invertible neural networks generators, we design corresponding discriminators (which are often neural nets of specific architectures) such that the Integral Probability Metric (IPM) induced by the discriminators can provably approximate the Wasserstein distance and/or KL-divergence. This implies that if the training is successful, then the learned distribution is close to the true distribution in Wasserstein distance or KL divergence, and thus cannot drop modes. Our preliminary experiments show that on synthetic datasets the test IPM is well correlated with KL divergence, indicating that the lack of diversity may be caused by the sub-optimality in optimization instead of statistical inefficiency.