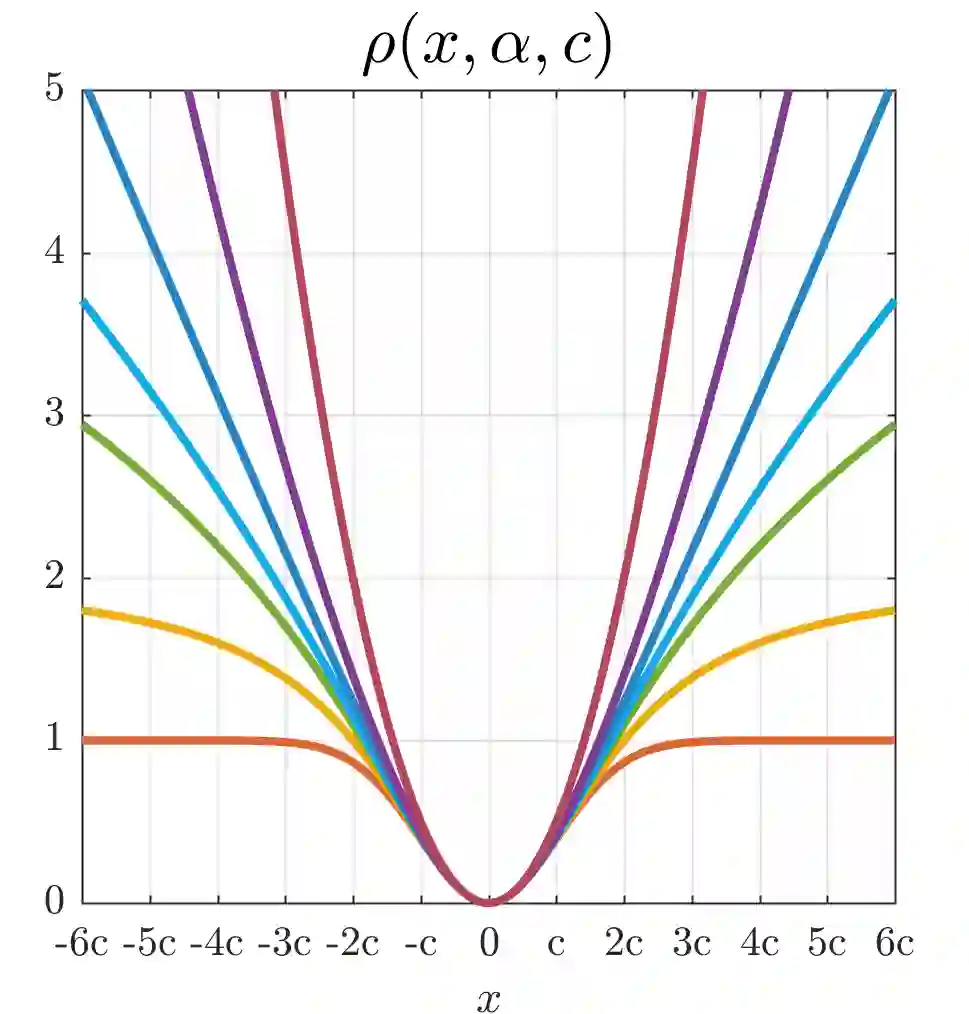
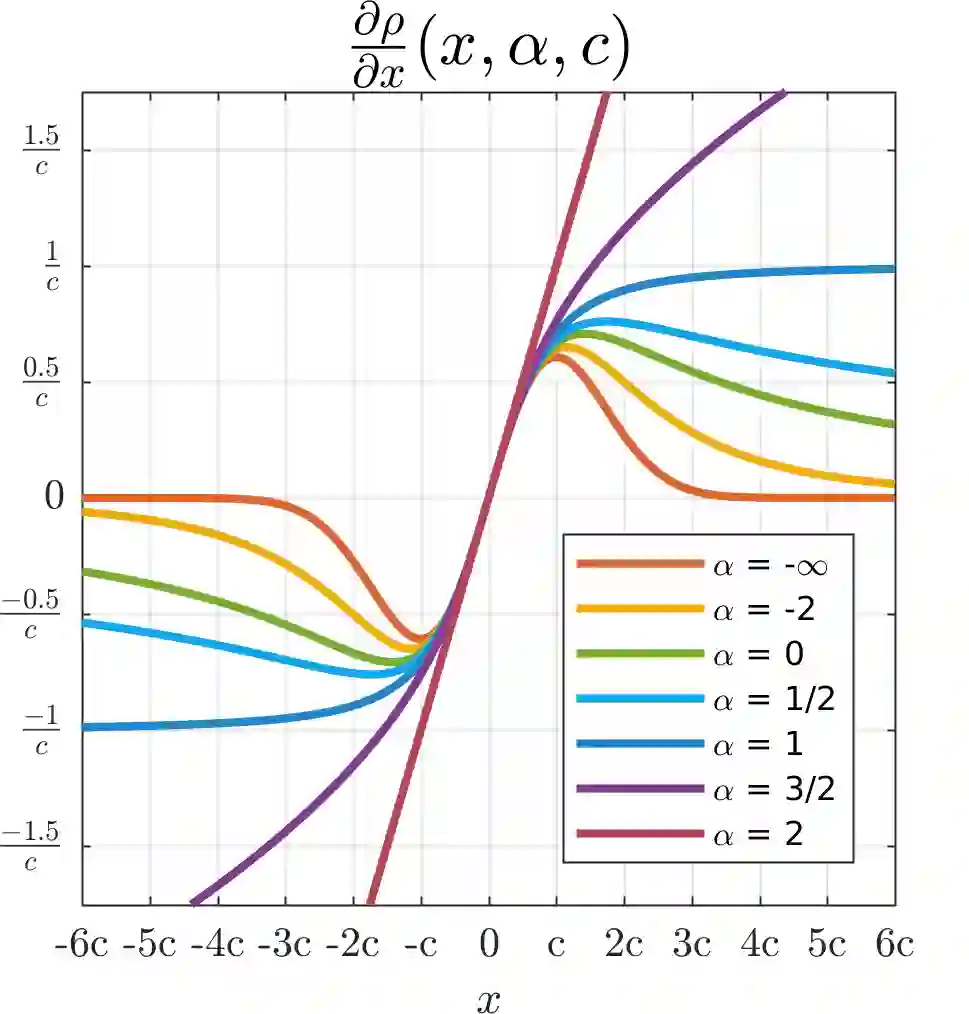
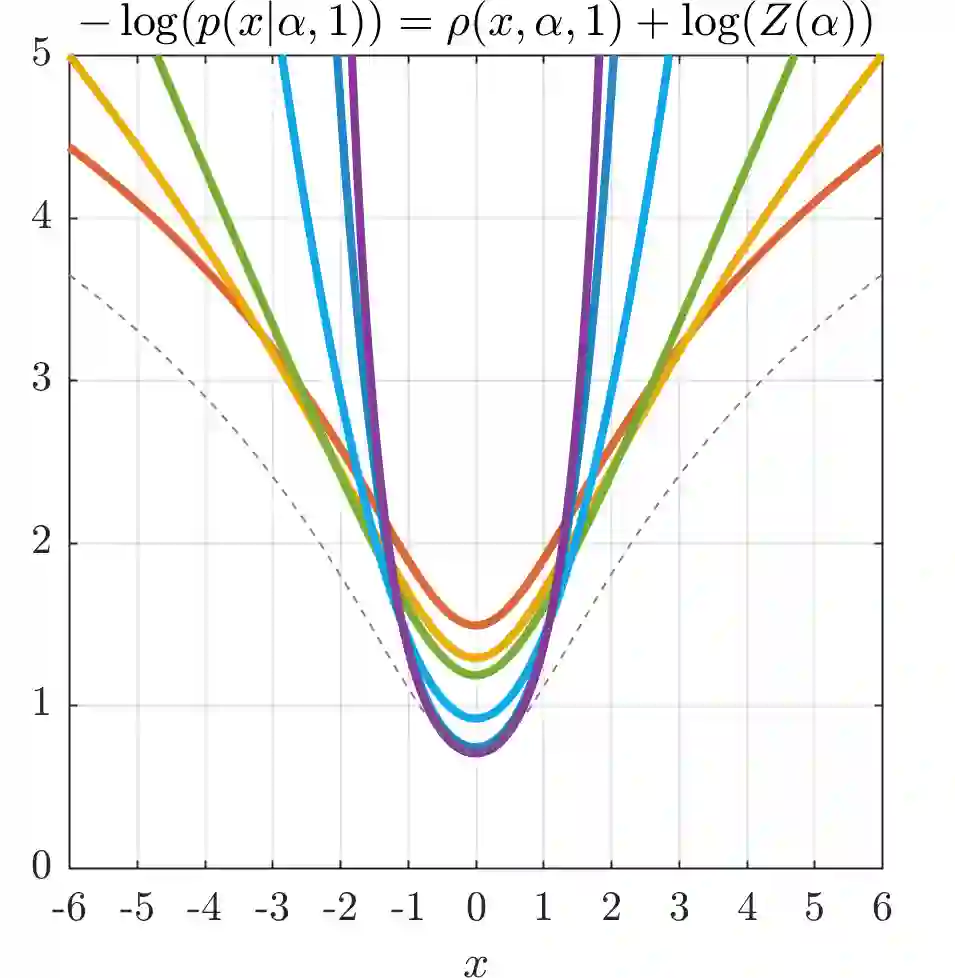
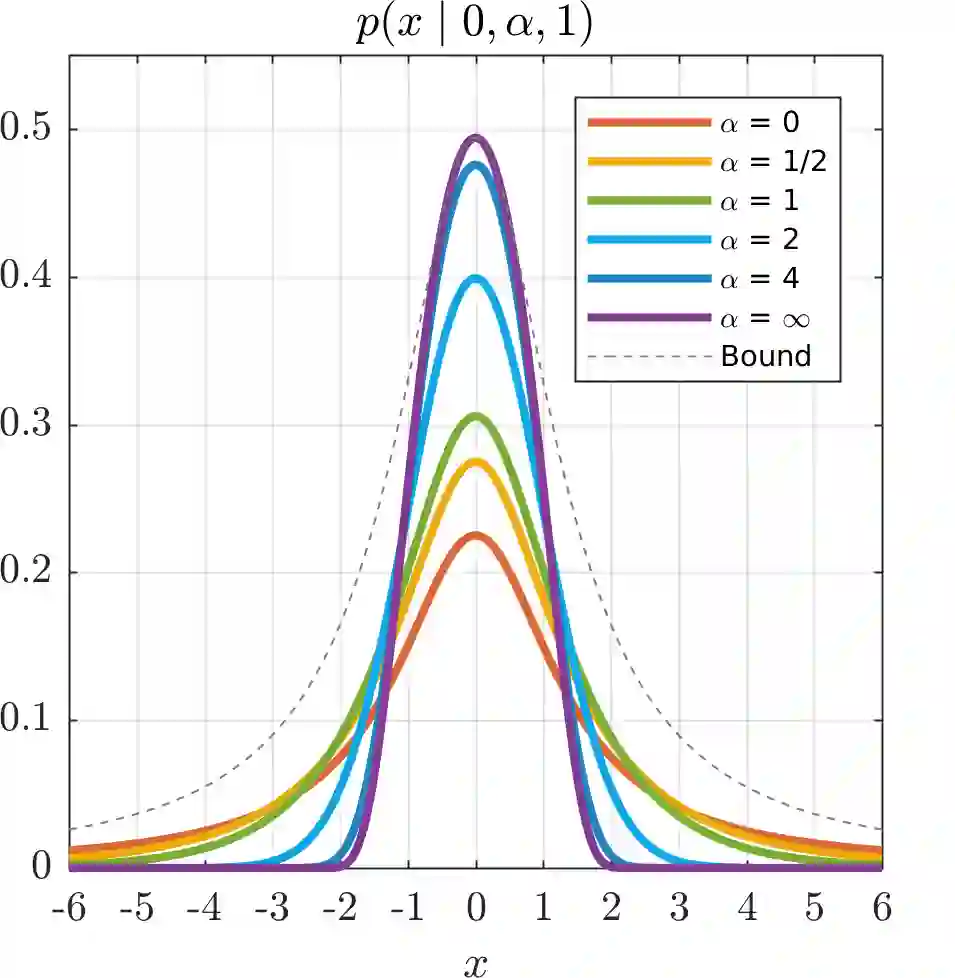
We present a generalization of the Cauchy/Lorentzian, Geman-McClure, Welsch/Leclerc, generalized Charbonnier, Charbonnier/pseudo-Huber/L1-L2, and L2 loss functions. By introducing robustness as a continous parameter, our loss function allows algorithms built around robust loss minimization to be generalized, which improves performance on basic vision tasks such as registration and clustering. Interpreting our loss as the negative log of a univariate density yields a general probability distribution that includes normal and Cauchy distributions as special cases. This probabilistic interpretation enables the training of neural networks in which the robustness of the loss automatically adapts itself during training, which improves performance on learning-based tasks such as generative image synthesis and unsupervised monocular depth estimation, without requiring any manual parameter tuning.
翻译:我们介绍了Cauchy/Lorentzian、Geman-McClure、Welsch/Leclerc、Charbonnier、Charbonnier/peredo-Huber/L1-L2和L2损失功能的概括性。通过将稳健性作为连续参数,我们的损失功能使围绕稳健的损失最小化的算法得以普及,从而改进了登记和集群等基本愿景任务的业绩。将我们的损失解释为单体密度的负日志,产生一种普遍的概率分布,包括正常和Cauchy分布作为特殊情况。这种概率化解释使得能够培训神经网络,使损失的稳健性在培训期间自动调整自身,从而改进了基于学习的任务的绩效,例如基因图像合成和不统一的单体深度估计,而无需任何人工参数的调整。