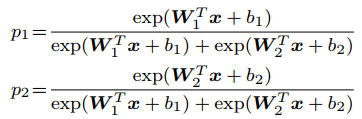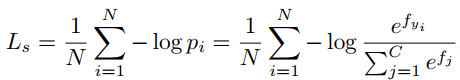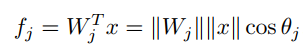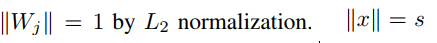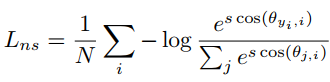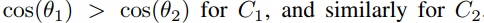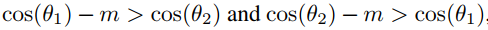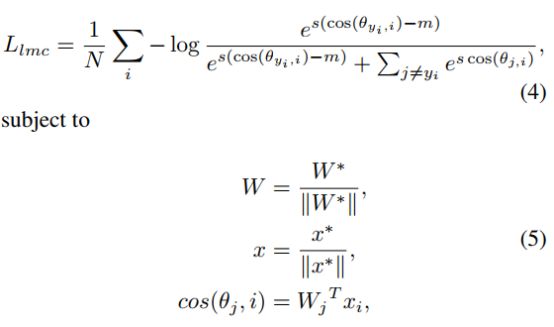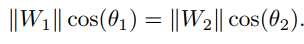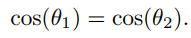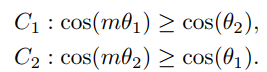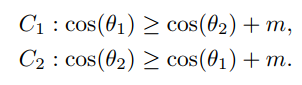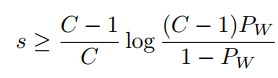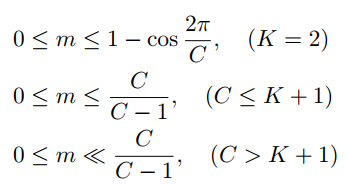CosFace: Large Margin Cosine Loss for Deep Face Recognition论文笔记

一、背景

在传统意义上的深度卷积神经网络的 softmax 代价函数的监督下，所学习的模型通常缺乏足够的判别性。为了解决这一问题，近期一系列损失函数被提出来，如 Center Loss、L-Softmax、A-Softmax。所有这些改进算法都基于一个核心思想： 增强类间差异并且减小类内差异。本文设计了一个新的损失函数，即增强边缘余弦损失函数 (LMCL)。更具体地说，通过对特征向量和权向量的 L2 归一化，把 softmax 损失函数转化为余弦损失函数，这样做消除了半径方向的变化，并在此基础上引入了一个余弦边缘值 m 来进一步最大化所学习的特征在角度空间的决策边界。

二、增强边缘余弦损失函数 (LMCL)

对于二分类问题，后验概率如下：

对应的softmax损失函数为：

令b=0，由向量内积公式可知

将w通过L2范数归一化，令||x||=s，即

将上式带入softmax损失函数可得如下公式，论文中称为NSL损失函数

 由上面的损失可知，该损失函数只能用来正确分类，即

由于判别性不强，引入了余弦间隔m（m>=0），即

带入NSL中，可得LMCL如下：

三、与不同损失函数的比较

（1）softmax

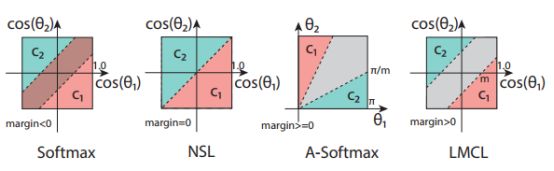
 决策边界如下，可以看出决策边界与W和角度都有关系，所以会导致分类间隔margin<0， 如图a所示，

（2）NSL

 先将W进行L2归一化，决策边界如下，此时分类间隔margin=0 ，如图b所示，

（3）A-softmax

将W进行L2归一化的前提下，引入了余弦间隔参数m。决策边界如下，此时分类间隔margin随角度减小而减小到0，如图c所示，

（4）LMCL

将W进行L2归一化的前提下，引入了余弦间隔参数m。决策边界如下，此时分类间隔恒等于 √2m，如图d所示。

四、对 LMCL 的理论分析

对于LMCL中的参数s和m，论文给了详细的推导，其中C为类别数，K为特征维度，如下：

五、实验

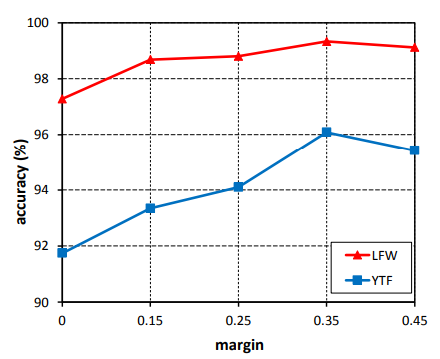
（1）在 LFW 和 YTF 上，具有不同边缘参数值 m 的 CosFace 的表现（%）

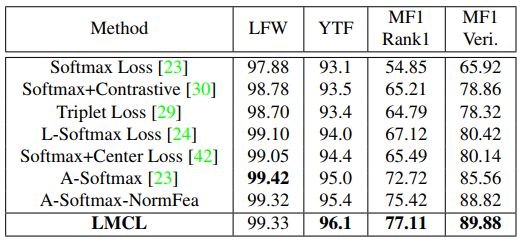
（2）论文提出的LMCL 与人脸识别社区当前最佳的损失函数的比较实验

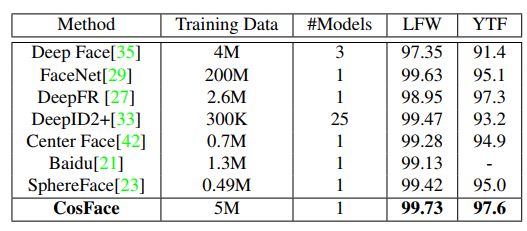
（3）在 LFW 和 YTF 数据集上的人脸验证表现（%）。#Models 表示评估方法中所使用的模型的数量。

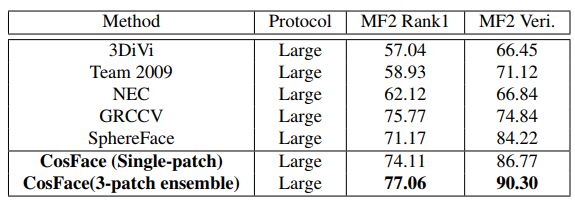
（4）在 Megaface Challenge 2 (MF2) 上的人脸辨识和人脸验证评估。