《Advances in Graph Neural Networks》第1~2章读书笔记
本书是由GAMMA Lab实验室推出,全面介绍了图神经网络的基础和前沿问题,主要分为以下三个部分:
Part 1:GNNs的基本定义和发展(Chaps. 1 - 2);
我们首先概述了不同图的基本概念,以及图神经网络的发展,包括几个典型的图神经网络。这一部分将帮助读者迅速了解这个领域的整体发展。特别是在第1章,将总结基本概念和定义,以及图神经网络的发展。第二章将介绍基本的图神经网络,包括GCN,GAT,GraphSAGE,HAN等。 Part 2:GNNs的前沿课题(Chaps. 3 - 7);
我们接着对有代表性的图神经网络技术进行了深入而详细的介绍。该部分将帮助读者了解该领域的基本问题,并说明如何为这些问题设计高级图神经网络。特别是第三章讨论了同质图神经网络,包括多通道图神经网络等。第4章介绍了异质图神经网络,主要集中在异质图传播网络等。之后,我们在第五章中介绍了动态图神经网络,其中考虑了时态图、动态异质 Hawkes process和时态异质图。然后,在第六章中,我们介绍了双曲图神经网络,包括双曲图注意网络和洛伦兹图卷积神经网络等。最后,第七章介绍了蒸馏图神经网络,包括图神经网络的知识蒸馏和对抗性知识蒸馏等。 Part 3:GNNs的未来发展方向(Chaps. 8)。
我们做出结论并讨论了未来的研究方向。尽管有大量的图神经网络方法被提出,许多重要的开放性问题仍然没有得到很好的探索,例如图神经网络的鲁棒性和公平性。当图神经网络被应用于现实世界的应用,特别是一些风险敏感的领域时,这些问题仍需要被仔细考虑仔细考虑。 📖一言以蔽之,本书从图表示学习的基础知识开始,广泛地介绍了GNNs的前沿研究方向,包括heterogeneous GNNs, dynamic GNNs, hyperbolic GNNs, distilling GNNs等。一方面基本知识可以帮助读者迅速了解GNNs的优点,另一方面各种前沿GNNs则有望激发读者开发自己的模型。相信,无论是初学者还是来自学术界或工业界的研究人员,相信都会从本书的内容中受益。
本文主要聚焦于Part 1,简要介绍GNNs的基本定义和发展,并帮助读者快速回顾GNNs经典模型。
(其余章节会在GAMMA Lab公众号持续更新,希望能与读者一同在本书中获益🥰)
✏️chapter 1-简要介绍
1.1 基本概念
1.1.1 图的定义和属性
-
图一般被定义为
-
邻接矩阵A一般用于描述图中边的分布
-
邻居,一般指一阶邻居节点 的邻居集合可以表示为 ,这里表示的是无向图,类似的还可以定义有向图出边邻居,入边邻居
-
节点的度,一般可以由临界矩阵行(列)求和得到
同时 ,这里表示的是无向图,类似的还可以定义有向图出度,入度。
-
拉普拉斯矩阵(Laplacian)定义为 -
相应地,有标准化形式的拉普拉斯矩阵(Normalized Laplacian),一般记作 或者 :
1.1.2 复杂图
-
异质图(Heterogeneous Graph)
一般可以简单认为是含有多个类型的节点,多个类型的边组成的图,数学定义为每个节点v和每条边e与其类型相关联的映射函数
-
元路径(Meta-path)
给定一个异质图 ,一条Meta-path 可以被定义为 , 表示特定类型的节点和边,这种新的关系 可以定义为
-
元图(Meta-graph)
元图 可以视为一个具有共同节点的多条元路径有向无环图(DAG)。
形式上,元图可以被定义为 ,对于所有的 ,都有 所有的 ,都有
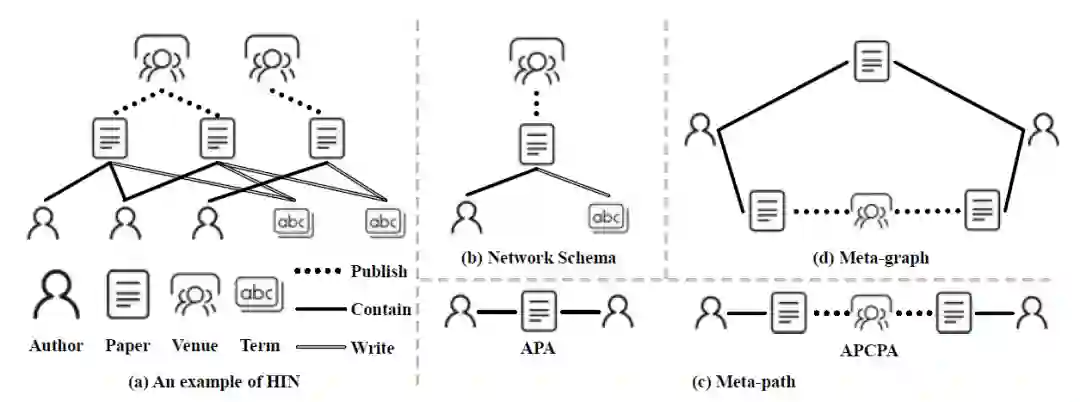
"APA"的meta-path表示一篇论文共同作者的关系;"APCPA"代表两作者在同一会议发表过文章关系。
两者都可以用来制定作者之间的接近关系。并且,元图可以是对称的或不对称的。
-
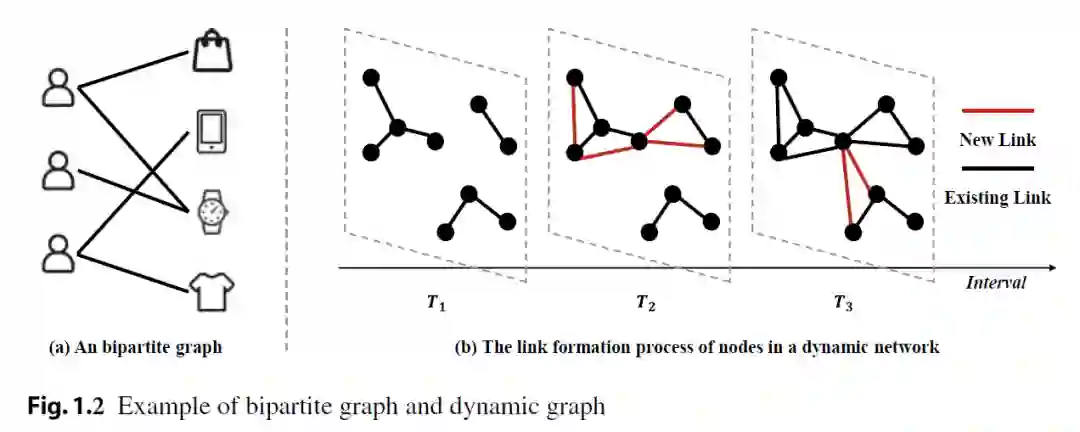
二部图(Bipartite Graph)
一个二部图 ,其中 包含两个不相交的子集 ,并且 , 所以对所有的边 ,都有 .
-
动态图(Dynamic Graph)
一个动态图 ,其中 是随时间动态改变的。具体来说,每个节点或每条边有一个时间戳信息,表明它们出现的时间。
1.2 图上的计算任务
-
对于不同的计算任务,它们主要可以分为两类
-
如图分类、图匹配和图生成(如用于药物发现)。 -
如节点分类、节点排名、链接预测、社区检测等。 -
一类是以节点为中心的任务,整个数据通常被表示为一个图,节点为数据样本。
-
另一种是以图为中心的任务,数据通常由一组图组成,每个数据样本就是一个图。
1.3 图神经网络的发展
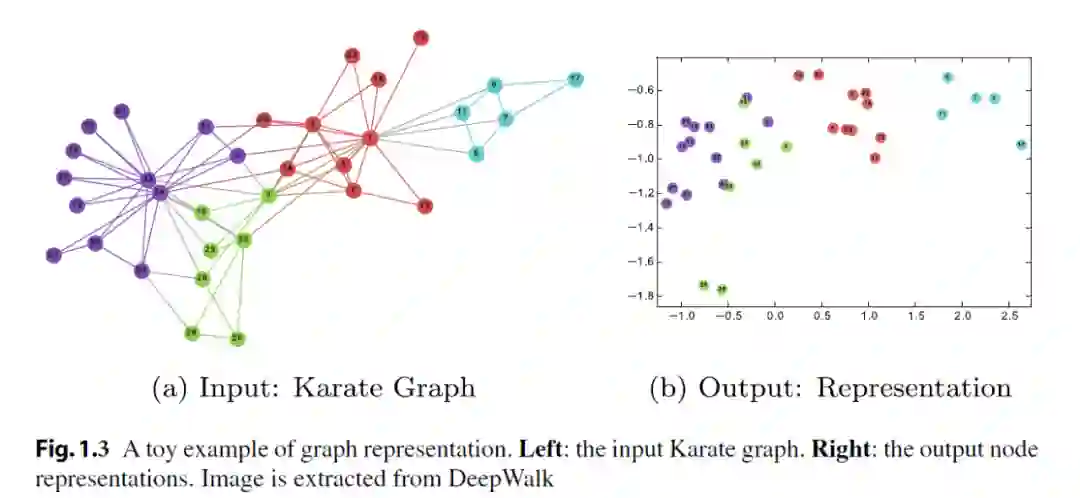
在过去的几十年里,它得到了很大的发展,可以大致分为三代,包括传统图嵌入、现代图嵌入和图上深度学习。
-
例如,DeepWalk是一种结合了random walk和word2vec的图表示学习算法。
-
图神经网络(GNN)可以大致分为空域方法和谱域方法
-
频谱方法通过利用图傅里叶变换和反图傅里叶变换的优势来利用图的谱信息。它们主要侧重于设计图谱滤波算子,可用于过滤输入信号的某些频率。如从谱域的GCN理解。 -
基于空域的发放执行涉及邻居的空间信息聚合。这些方法明确地利用图的结构信息。如从空域的GCN理解 ,GAT ,GraphSAGE。
✒️chapter 2-Fundamental Graph Neural Networks
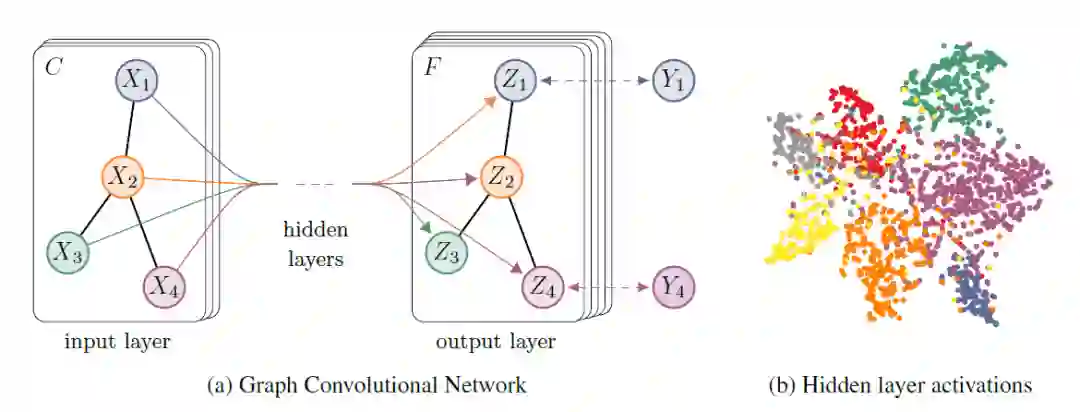
在CNN的启发下,图卷积网络(GCN)被提出来,将卷积操作从网格数据推广到图数据,并导致图领域的突破。作为基本的GNN,GCN在基于频谱(从图信号处理的角度)和基于空间(从信息传播的角度)的卷积GNN之间架起了桥梁。
基于空域的GCN(从消息传播的角度)指出GCN的本质的本质是迭代地聚合邻居的信息; 基于谱域的GCN将傅里叶变换引入图信号处理,将GCN看作一个低通滤波器。
2.1 Graph Convolutional Network (GCN)
谱域角度
谱域的图卷积可以被定义为一个信号 (每个节点由一个标量表示)与一个滤波器 的乘积,可以写成
,其中 是标准化后的拉普拉斯矩阵 ,通常定义 是特征值的函数,即 .
由于对拉普拉斯矩阵L的特征分解开销较大,一般用切比雪夫多项式去逼近,切比雪夫多项式的递推定义如下
从而, .
GCN的简单推导如下:(使用了切比雪夫多项式的一阶近似,K=1)
空域角度
空域的图卷积一般被定义为消息传递(MessagePassing),
-
GCN:http://arxiv.org/abs/1609.02907
2.2 Graph SAmple and aggreGatE (GraphSAGE)
-
transductive learning(转导学习),指所有的数据在训练阶段都可以拿到,学习过程是在固定的数据上,一旦数据发生改变,需要重新进行学习训练,典型的比如图上的随机游走算法,一旦图数据发生变动,所有节点的表示学习都需要重新进行。 -
inductive learning(归纳学习),指可以对在训练阶段不可见的数据(在图数据中,可以指新的节点,也可以指新的图)直接进行预测而不需要重新训练学习方法
GCN被设计为从一个固定的图中学习每个节点的良好表示。
对于大规模的图来说,训练过程在内存方面可能是昂贵的。
GNN的主要问题是它们缺乏对未见过的数据的概括能力。而且,它必须为新的节点重新训练模型以表示这个节点。
GraphSAGE计算过程中完全没有拉普拉斯矩阵的参与,每个节点的特征学习过程仅仅只与其K阶邻居相关,而不需要考虑全图的结构信息。对于新出现的节点数据,只需要遍历得到K阶子图,就可以代入模型进行相关预测。
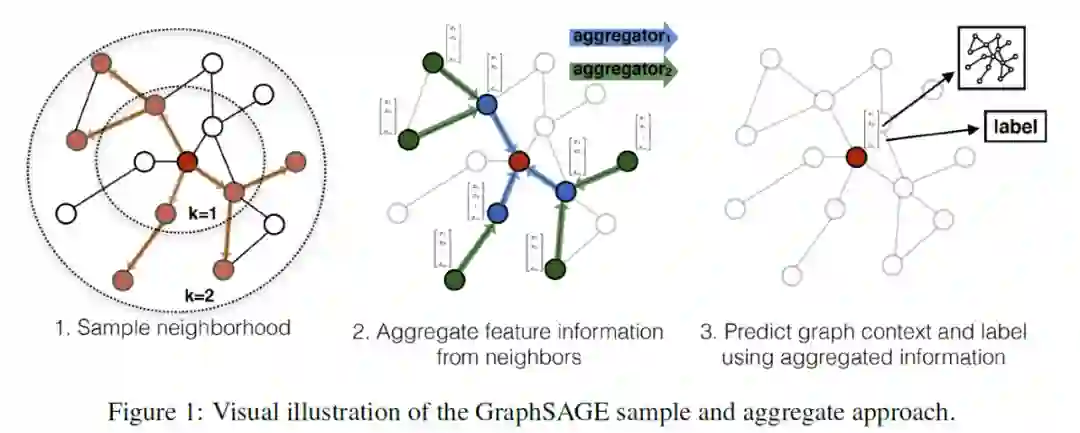
上述,算法的基本思路是先 将小批量集合B内的中心节点聚合操作要涉及到的k阶子图一次性全部遍历出来,然后在这些节点上进行 K 次聚合操作的迭代计算。
【Sampling时,从内到外,得到k阶子图(由于每层设置的有邻居采样倍率,所以一般来说是非完全子图),
Aggregate时,从外到内,生成 minibatch B 所有节点最终的特征表示】
-
GraphSAGE:http://arxiv.org/abs/1706.02216
2.3 Graph Attention Network (GAT)
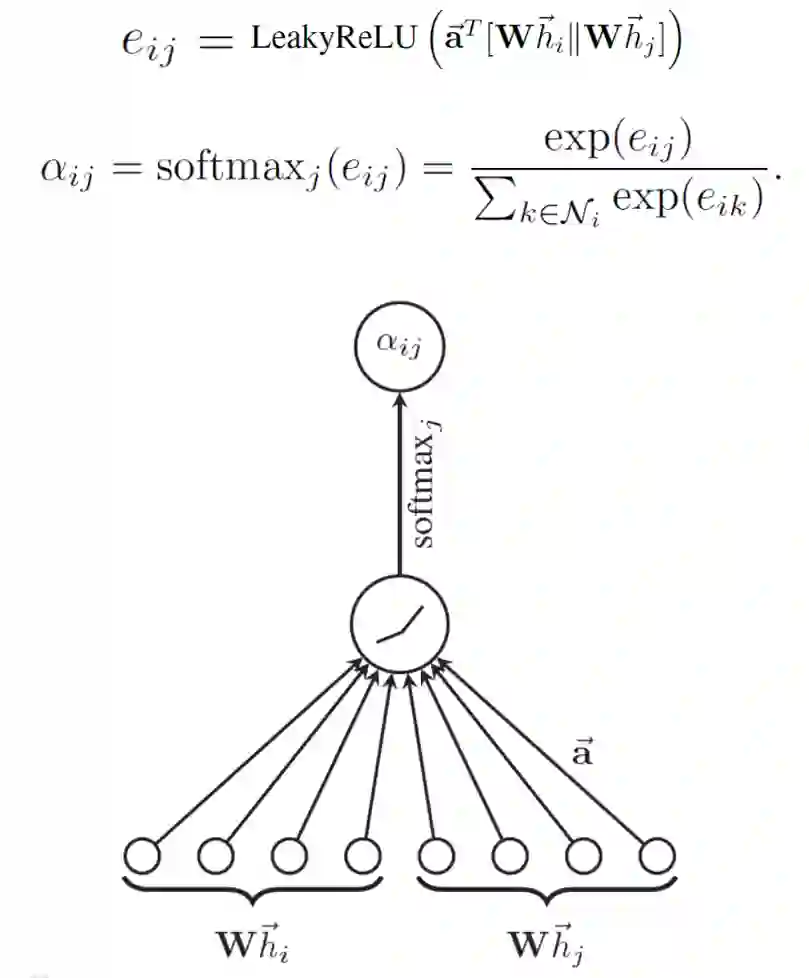
GAT通过引入注意力机制来聚合邻居,从而扩展了GCN.
-
注意力机制
为了获得足够的表达能力将输入特征转化为更高层次的特征,至少需要一个可学习的线性变换。GAT中,每层使用一个可训练的共享的线性变换矩阵 和权重向量 。
-
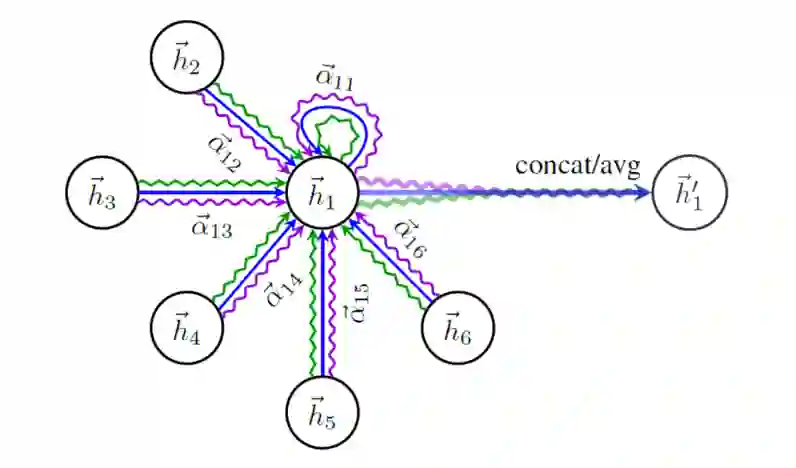
多头注意力
-
多头注意力机制的引入,同样与transformer相似,用Muti-Head Attention来模拟CNN多输出通道的效果。以求学习到更多层次的表达。GAT原文中,除最后一层muti-head attention取avg外,其余均concat.
-
GAT:http://arxiv.org/abs/1710.10903
2.4 Heterogeneous Graph Attention Network (HAN)
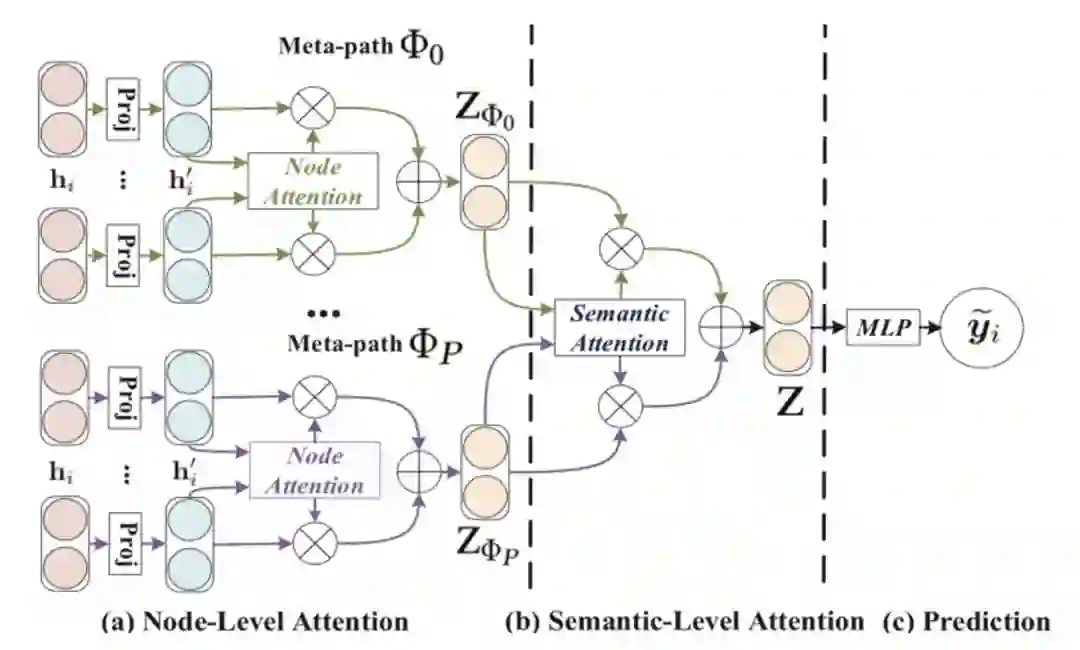
在这部分,我们介绍HAN,它通过利用节点级注意力和语义级注意力来学习节点和元路径的重要性,为异构图扩展了GCN。因此,HAN可以捕获异构背后的复杂结构和丰富的语义。
HAN
-
利用元路径将异质图分割成几个同质图,在每个同质图内应用节点级别的注意力机制生成节点表示。 -
然后再通过一次语义级别的注意力机制去关注基于每个Meta-path的同质图间的节点表示,进而生成最终的节点表示。
-
HAN:http://arxiv.org/abs/1903.07293
专知便捷查看
便捷下载,请关注专知公众号(点击上方蓝色专知关注)
后台回复“图神经网络” 就可以获取《图神经网络合集资料》专知下载链接