图机器学习 2.2-2.4 Properties of Networks, Random Graph

图机器学习 2.1 Properties of Networks, Random Graph

本文继续学习斯坦福CS224W 图机器学习的第二课~

前面介绍了用来衡量一个图模型的几个主要属性，并且应用于实际中：msn人际关系图和PPI网络之后发现一些属性的值很接近

特殊->一般->建立模型

那么现在考虑一般情况下的模型：考虑最简单的图模型

【注意这里考虑的是无向图】我们用G_{np}来表示具有n个节点且每个边(u,v)都是服从概率p的独立同分布的无向图

img

【注意】n和p不能唯一决定图模型！

也就是说图其实是随机过程的一个结果，下图是给定n,p值的一个例子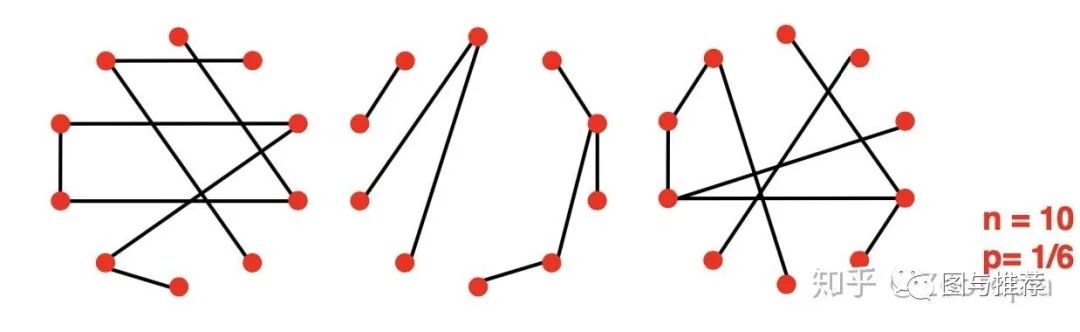

img

那么现在对于这么general的一个图，我们来看看前面提到的那些属性的值是多少

（1）度分布（degree distribution)

img

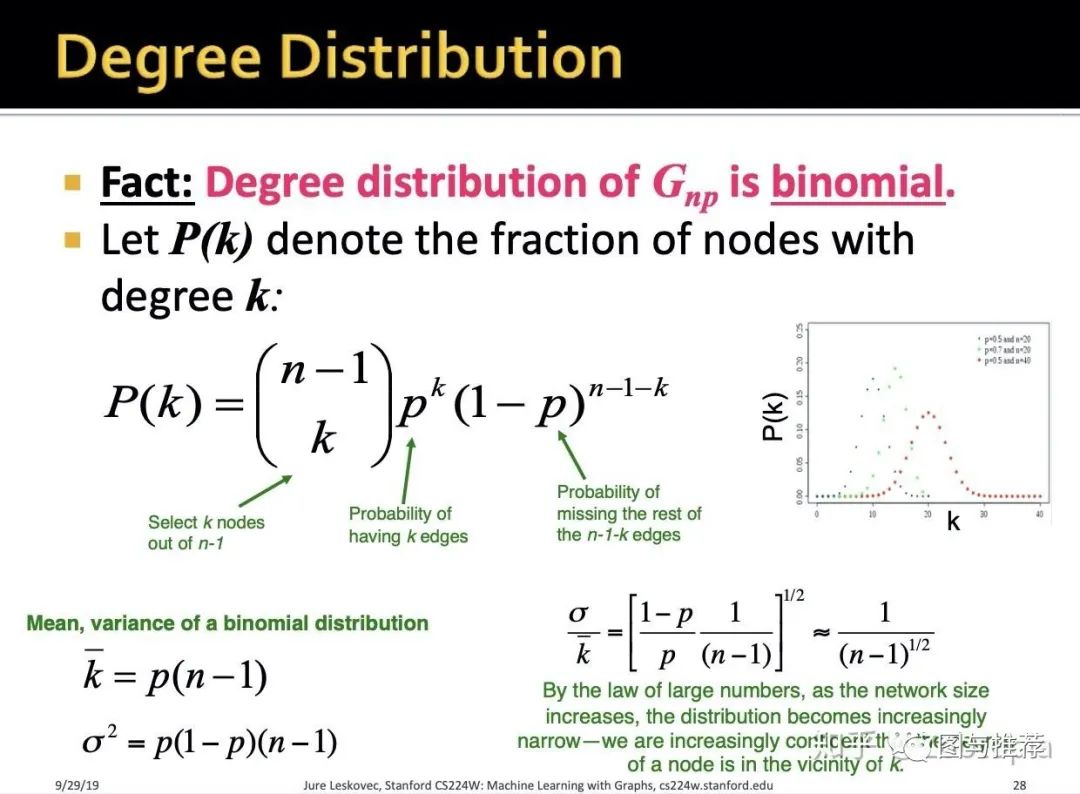
• P(k)：选定了一个节点，于是图中剩下n-1个节点，从剩下的节点中选取k个节点乘以这k个节点有k个边（也就是度为k）的概率
• 有了度分布，可以发现其是 二项式的
• 既然是二项式的我们就能得到其期望和方差

img

方差和期望的比值说明：当网络规模逐渐变大，平均值会越来越集中

对应了大数定理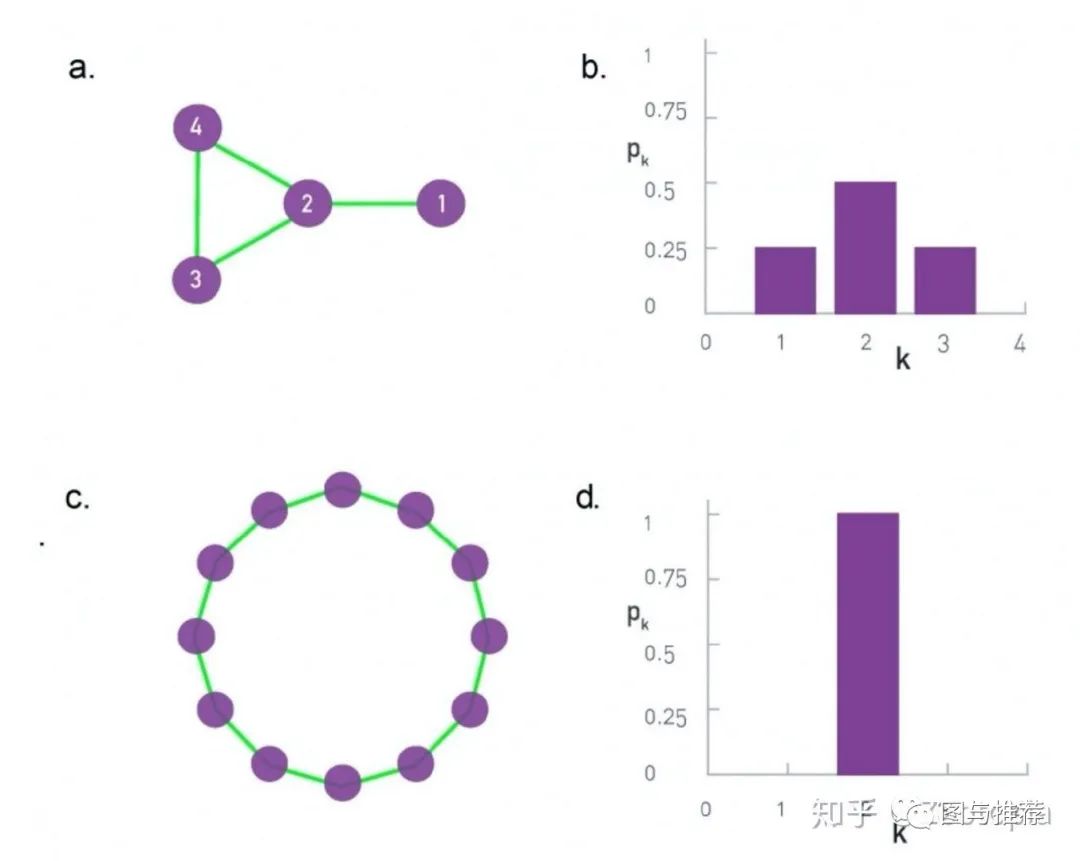

img

补充上一节的一个内容：注意到度的直方图有利于我们判断图的结构

（2）聚合系数

img

这里的计算比较显然，但是注意到E[Ci]可以发现当期望是一个固定值时，随着图规模越来越大，随机图的聚合系数会趋近于0。

【下面的学习部分，需要记住随机图的聚合系数是p】

讨论完了度分布和聚合系数，下面来看随机图的路径长度，这里通过“扩展(expansion）“来衡量

（3）expansion

什么是扩展数？

img

简单理解为：任取图中节点的一个子集，相对应的从子集中离开的（也就是和这些节点相关的）最小节点数目

或者还可以理解为：为了让图中一些节点不具备连接性，需要cut掉图中至少多少条边？

（answer：需要至少cut掉alpha Num(节点）条edges）

扩展数alpha也是一个用来衡量鲁棒性的一个度量

（4）largest connected component（最大连接元）

什么是最大连接元？我们看下面这个图就一目了然

图中标红的部分就是最大连接元：连接最多节点的部分

图来源：

https://networkx.github.io/documentation/networkx-1.9/examples/drawing/giant_component.htmlnetworkx.github.io

最大连接元的用途/意义：展示随机图的“进化”过程

当聚合系数=0的时候：也就是没有edge，这时候是一个空图

当聚合系数=1度时候：就是一个“全连接”的图

那么当聚合系数从0变化到1的过程中发生了什么变化？【当平均度=1的时候，因为k=p(n-1),此时聚合系数c=p=1/（n-1），出现了一个大连接元，以此类推】

img

学习完了随机图中的四个重要属性，下面来看随机图的应用性如何，看看和MSN数据的对比

img

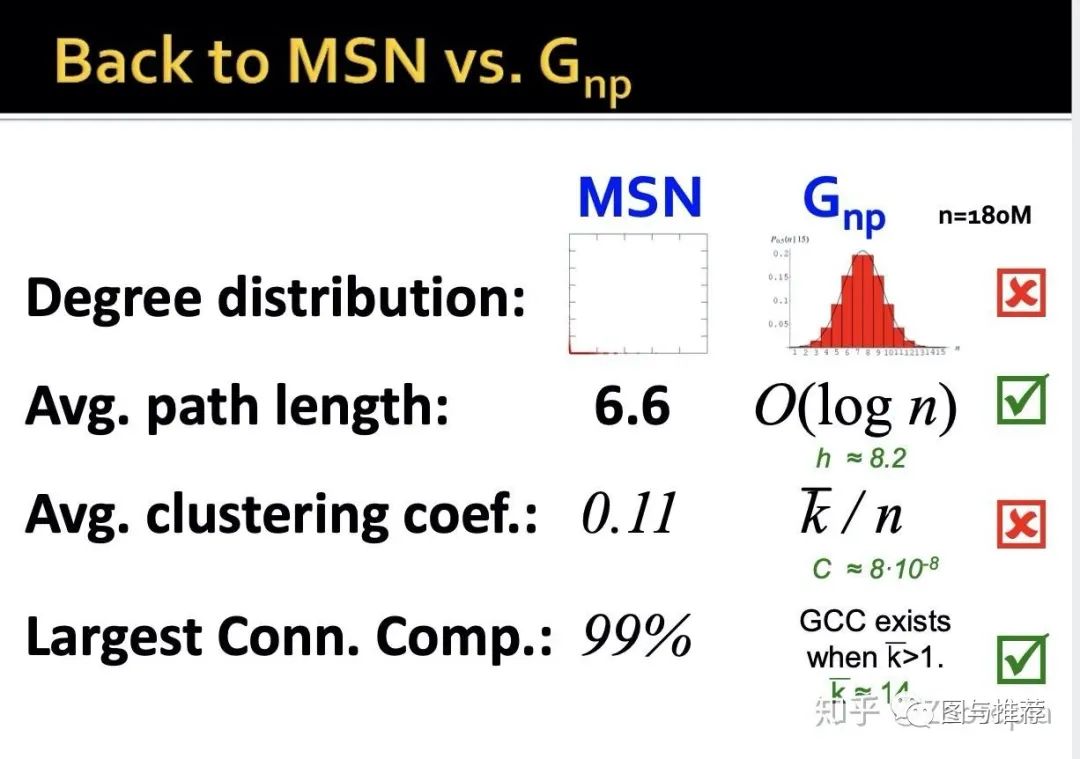
• 之前说过度分布的直方图有利于判断图的结构，MSN和随机图的直方图差距还是很大的；
• 平均路径：MSN和随机图的数据差不多
• 平均聚合系数：差距很大，随机图的非常小
• 最大连接元：很接近

综上来看，随机图的实际应用性如何？----不好！

img

从上面的属性比较可以看出：实际上的网络并不是随机的。

那么问题来了，既然如此又为什么要学习随机图呢？因为这是最简单也是最有效的学习和评估网络的方法！

随机性包罗万象，我们可以根据实际网络的特性来修改随机图来适应实际网络的需要

那么，如何让随机图实际应用性变强呢？

上一节说了随机图和实际网络还是有差距的：主要体现在聚合系数和度分布不一样

那么能不能对随机图进行一定的修改，使得重要的度量能和实际网络对应上呢？那么就要介绍这部分的主要内容：small-world model（我暂且翻译为小世界模型吧）

img

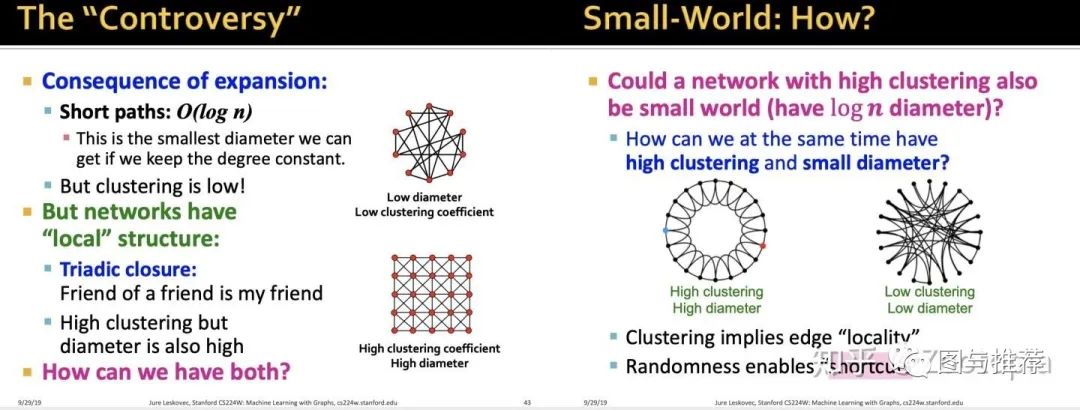
随机图的聚合系数很小，直径很大。这才是和真实网络最大的差异之处。所以能不能有【高聚合系数+小直径】？首先来分析聚合系数反应的本质是什么。

【高聚合系数反映了局部性】简单来说就是：社交网络中，我的朋友们互相也是认识的，如同下图

img

聚合系数和直径之间有一个矛盾之处在于：图的扩展（expansion）会使得保持度不变的情况下，直径越小也会导致聚合系数越小；而高聚合系数（高度连接的网络）却往往直径很大。那么怎么解决这个矛盾？基于以下两个思想：

（1）聚合反应局部性（2）随机性可以使得“捷径“出现

img

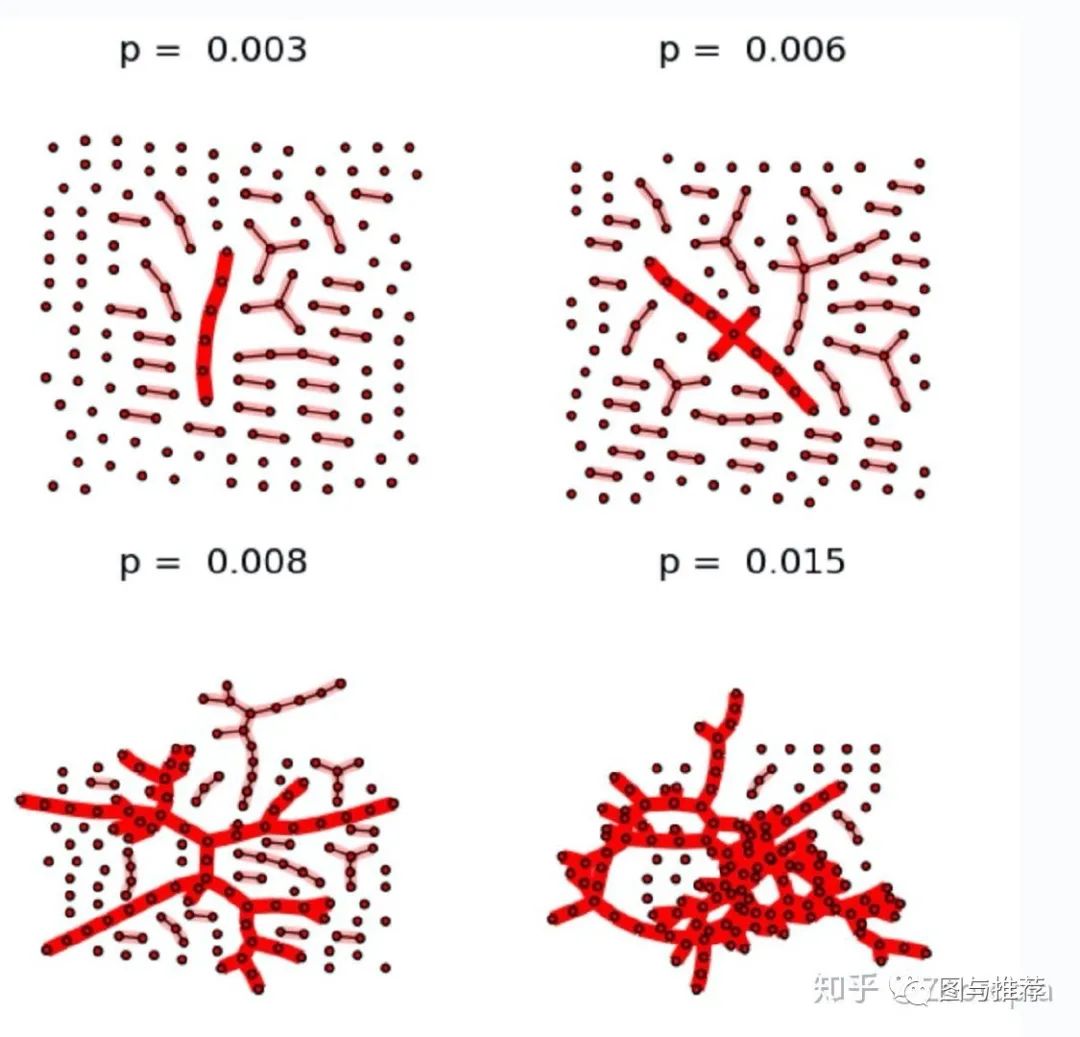
解决方案如下：

STEP 1：选择高聚合的网络

STEP 2：对每个边，以概率p修改边的终点（引入捷径）

img

这个“捷径”的方法很类似于数值计算中的“插值”：把节点作为插值节点，那么这里修改过的边就类似”线性插值“

从图上可以看出来，想要随机创造捷径是很简单不费力的。

反过来思考：聚合系数呢？社交网络中，我的朋友们互相也认识，所以聚合系数高，可是很难让我的朋友们互相“绝交”从而让聚合系数降下来。下图可以反应这个现象

横坐标是修改原有图的边位置的概率，纵坐标是聚合系数

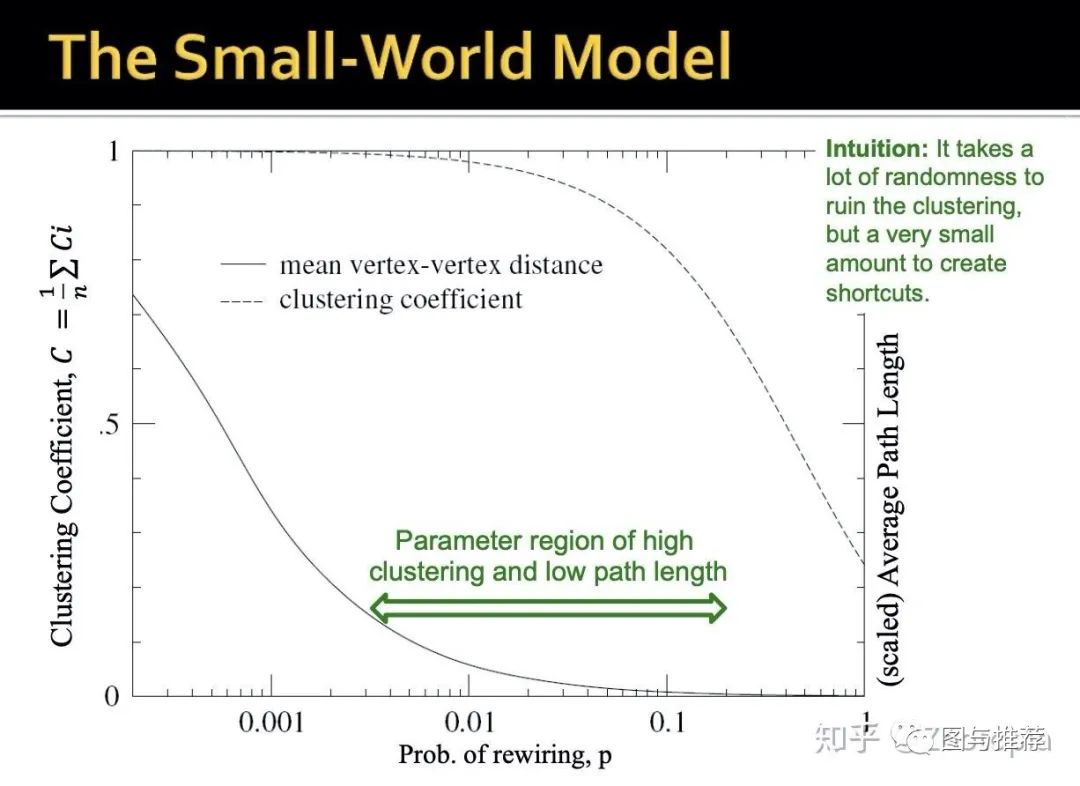
从图中可以看到“高聚合系数+低路径长度”的区域是很大的

既然已经解决了随机图和实际网络的"gap“，那么现在我们看看这个被修改了的随机图，表示的是什么？

（1）高聚合系数：我的大部分朋友们互相都认识（2）低直径：但是我也有几个朋友在另一个城市，且他们和其他朋友互不认识

实际网络这样的情况还是很多的

第二节课的最后一部分：Kronecker图模型

前面一直都是在讨论随机图，上一节还说到通过对随机图引入随机“捷径”可以将随机图变为small-world model，那么这部分来讲讲如何生成大的真实图。

首先开门见山介绍背后的idea：就是递归（循环）图生成

基于现实观察：自相似性

比如不同的friendship的建立往往基于相同的文化、相似的爱好等等

很多物体和本身的一部分是很类似的，那么利用这个思想，可以给定初始的小的图，从而对其进行不断的扩张得到递归图

img

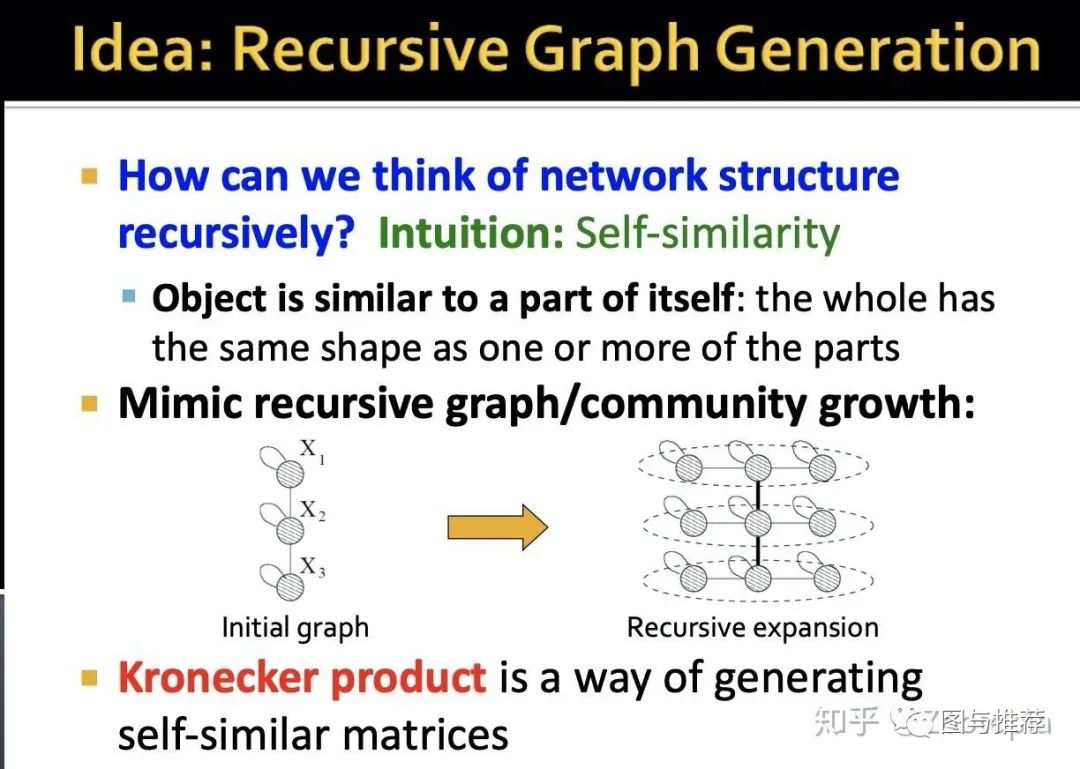
那么这个思想基于的工具是：kronecker积--定义如下

img

这个积的定义基本上大家在很多数学书上都有看到，这个积的结果是明显放大了原有的矩阵的阶。那么对于在图中的推广就是利用图的邻近矩阵来做kronecker积

那么什么是kronecker 图？--初始图（初始邻近矩阵）的循环kronecker积

img

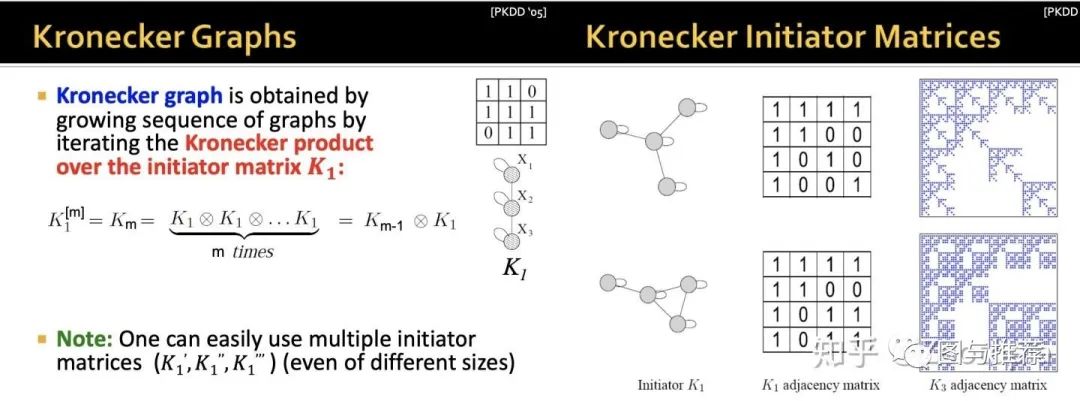
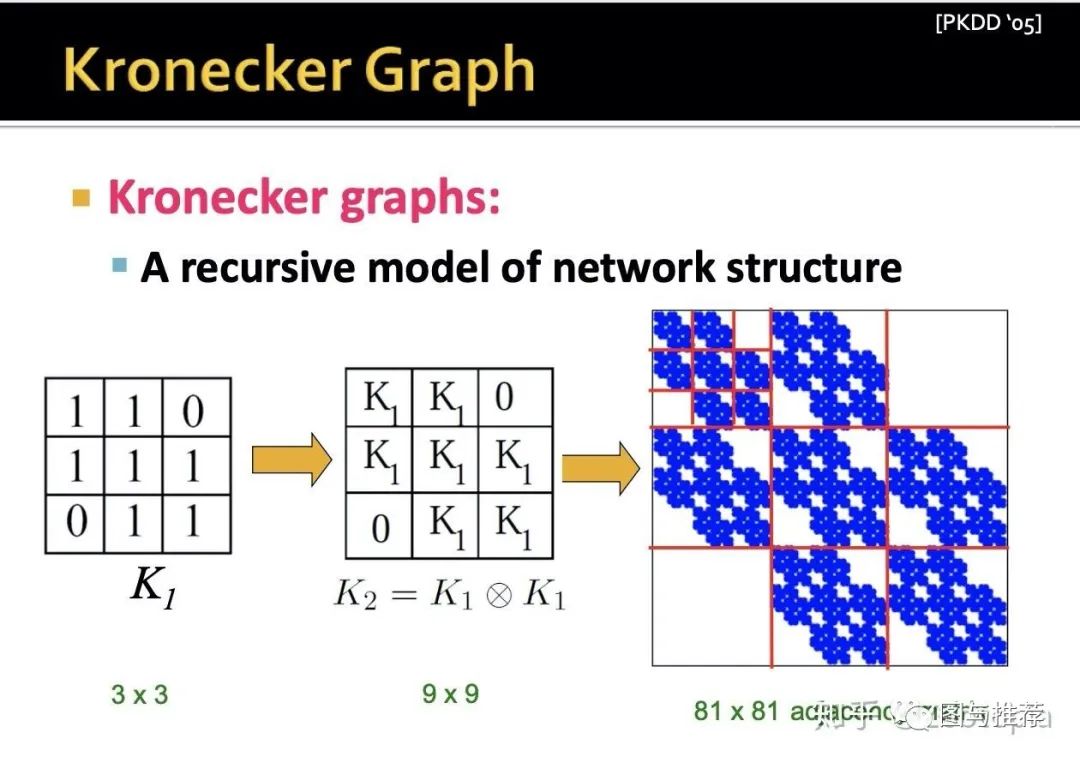
这样的方法即自然又简单，但是呢，我们观察下面这个图

img

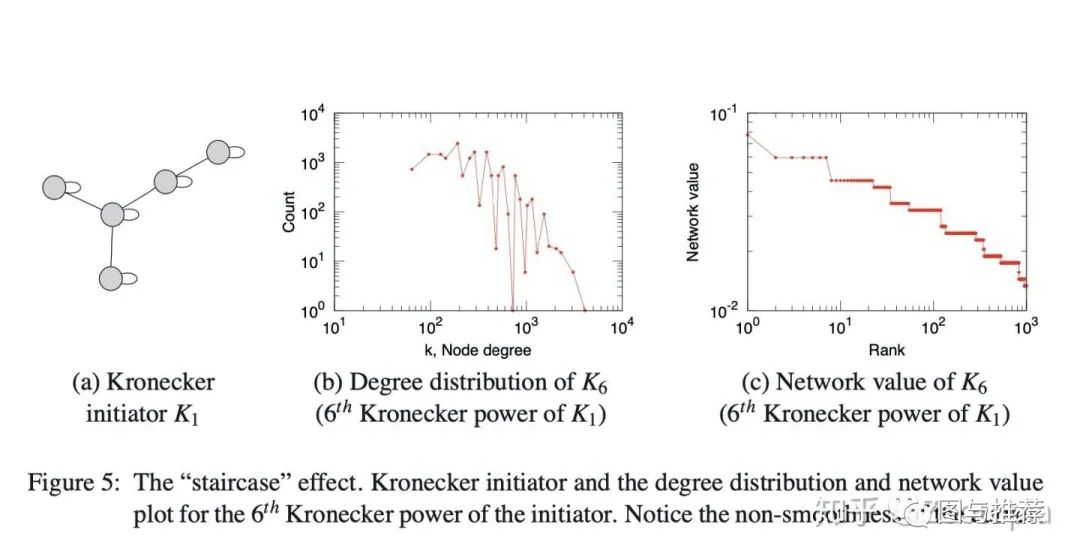
尽管到目前为止讨论的Kronecker结构产生的图具有一系列所需的特性，但其离散性质在程度和频谱数量上会产生“阶梯效应”，这仅仅是因为单个值具有较大的多重性。例如，图邻接矩阵的特征值的度分布和分布以及主要特征向量分量的分布（即“网络”值）都受此影响。这些数量是多重分布的，这导致具有多个重复的单个值。下图说明了阶梯效应（这部分来自lecture讲解人的论文https://dl.acm.org/doi/10.5555/1756006.1756039

img

会发现得到的图邻近矩阵的结构是很规则的（因为邻近矩阵的元素都是1或者0），类似于具有规则结构的网格一样，这样的当然好（利于我们分析），可是这样的图结构就很难capture真实复杂网络的信息了，那么要怎么办？-----答案是引入随机性！

这里在初始矩阵引入随机性的意思是：放松初始矩阵--邻近矩阵只有0或者1元素的条件，而是可以有[0,1]之间的元素，也就是

（1）初始矩阵的每个元素反应的是特定边出现的概率

（2）对初始矩阵进行Kronecker积运算，以获得较大的随机邻接矩阵，在该矩阵中，大型矩阵的每个元素数值再次给出了特定边出现在大图中的概率，这样的随机邻接矩阵定义了所有图的概率分布

img

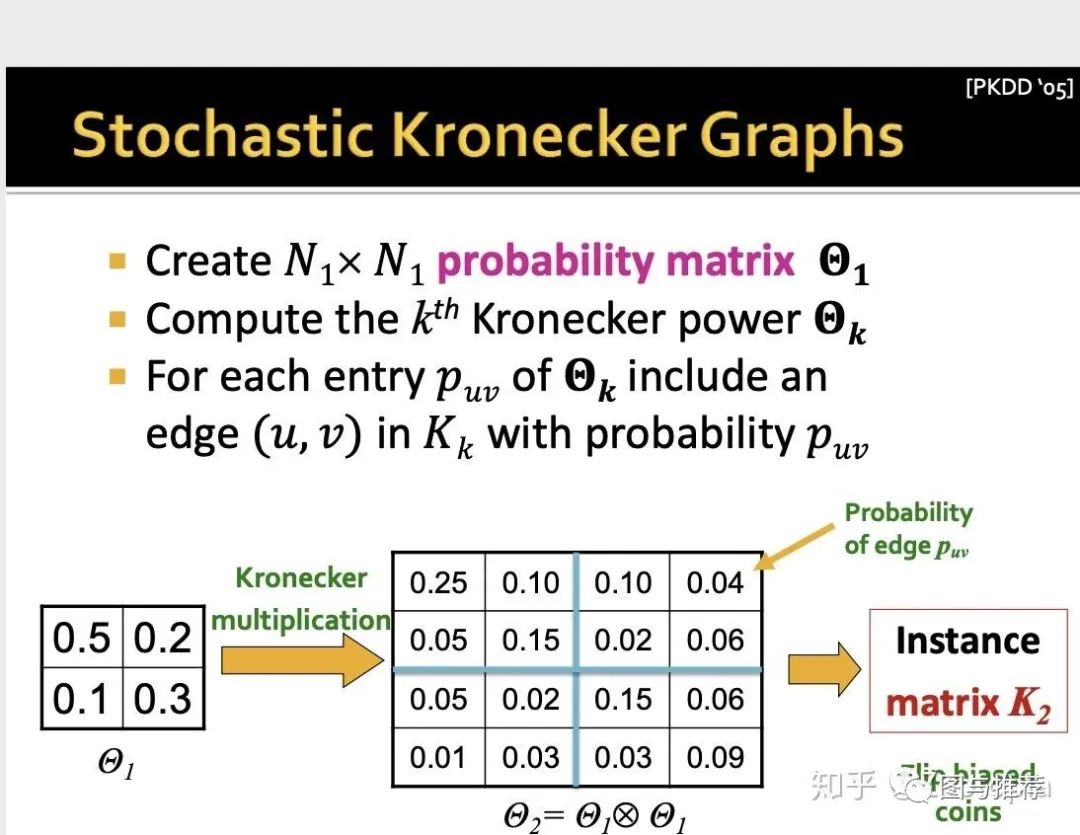
那么这个方法存在一个缺陷：费时间！

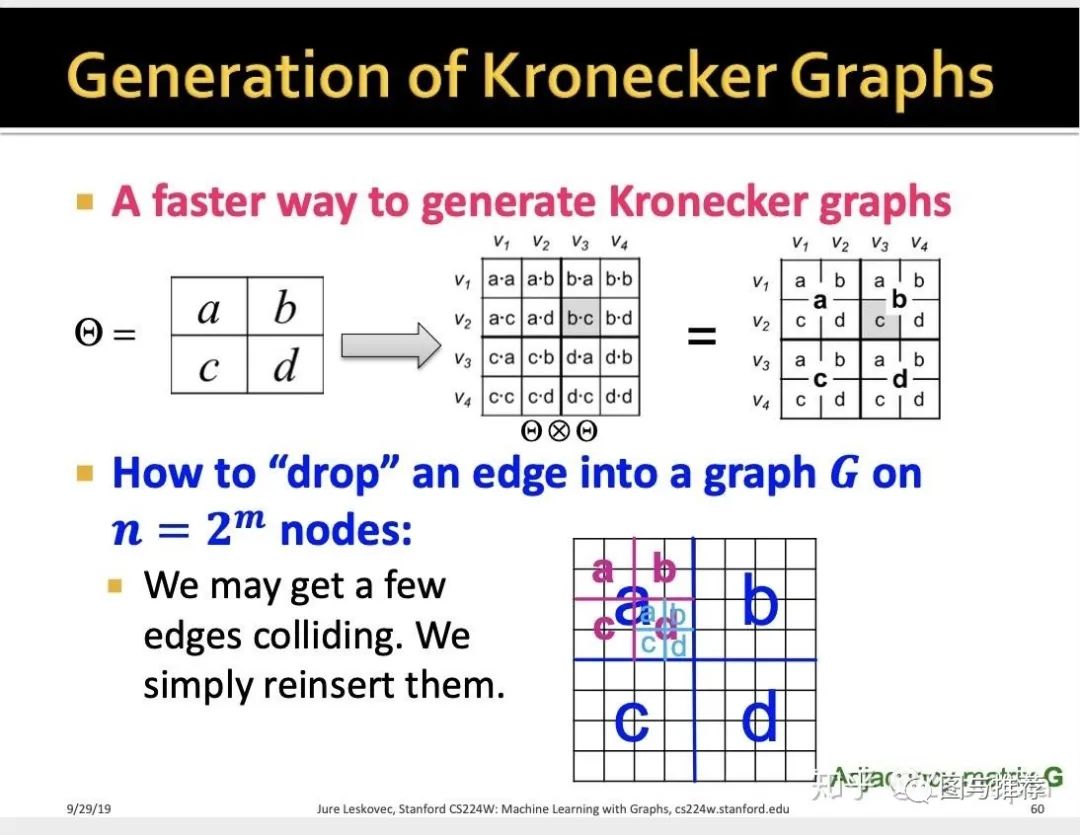
所以下面给出了一种快速方法---基于的思想：还是kronecker积的本质--循环性

img

img

img

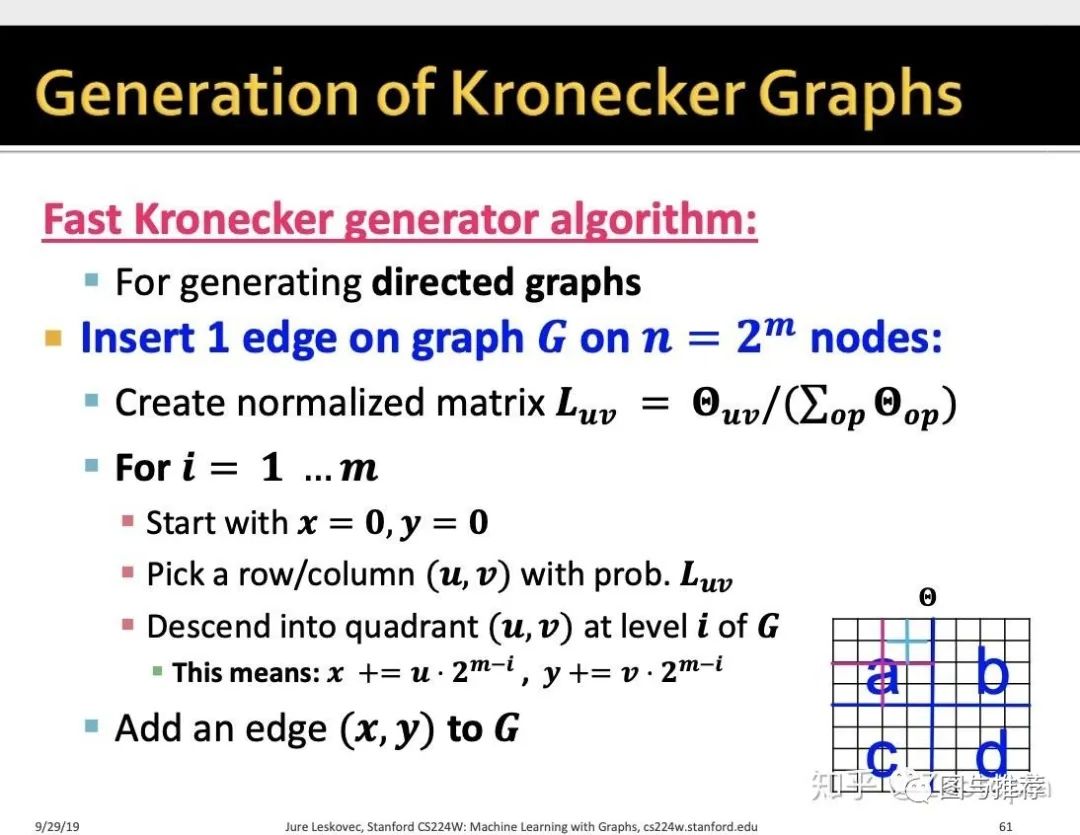
总结一下：随机kronerker图从数学上用公式来表示就是

img

img

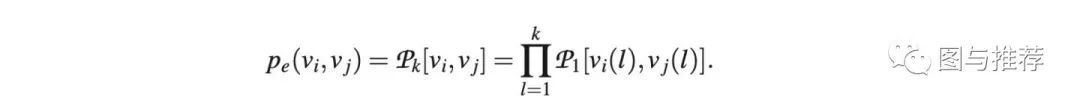
这给了我们对随机Kronecker图的非常自然的解释：每个节点由一系列分类属性值或特征来描述。然后，两个节点链接的可能性取决于各个属性相似性的乘积。