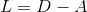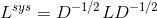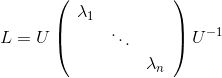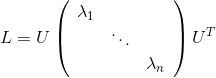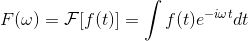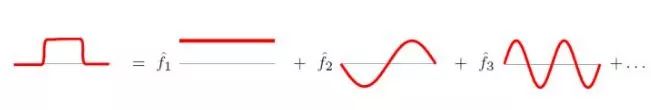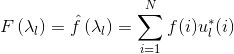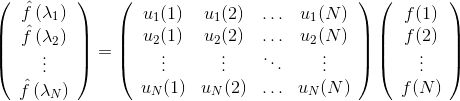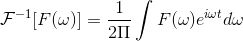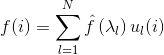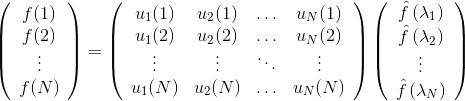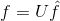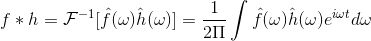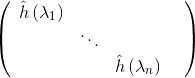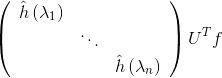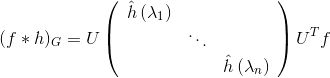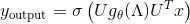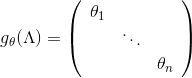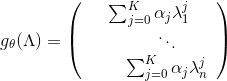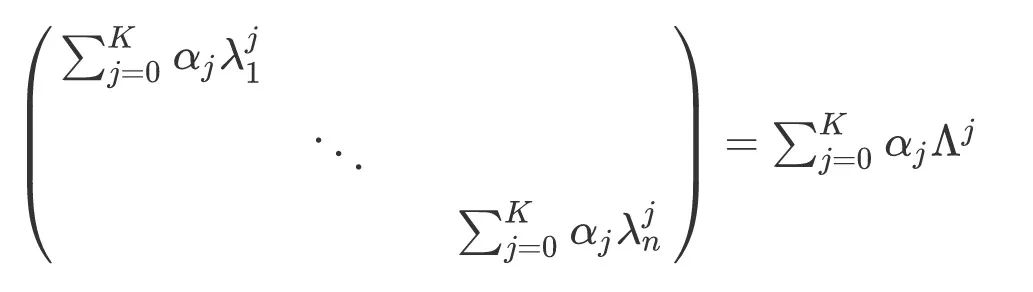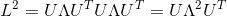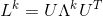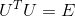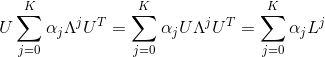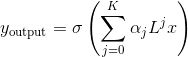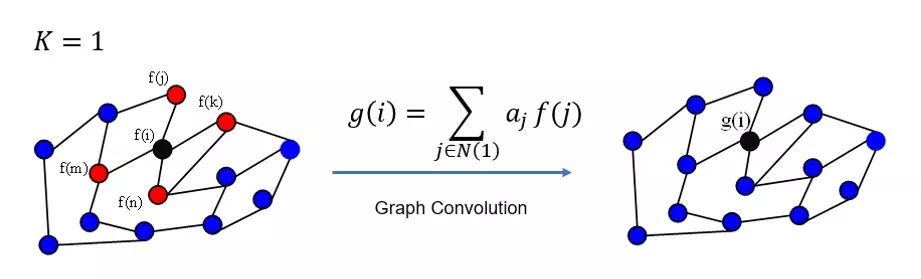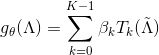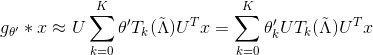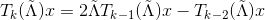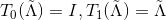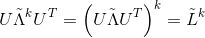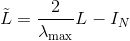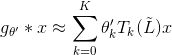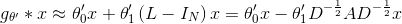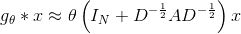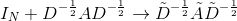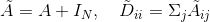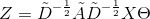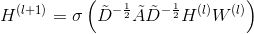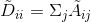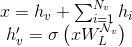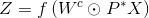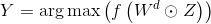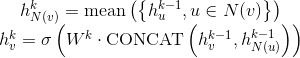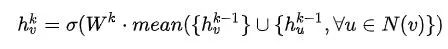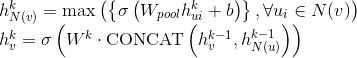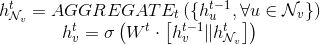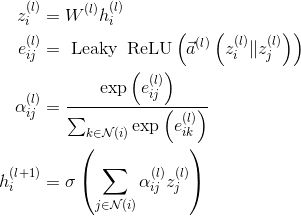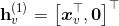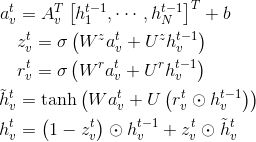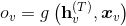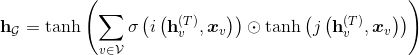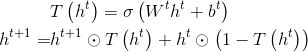Graph Neural Networks 综述

2019 年 8 月 13 日 计算机视觉life

点击上方“计算机视觉life”，选择“星标”

快速获得最新干货

深度学习一直都是被几大经典模型给统治着，如CNN、RNN等等，它们无论再计算机视觉CV还是自然语言处理NLP领域都取得了优异的效果。

针对CV领域，图像是一个二维的结构，于是人们发明了卷积神经网络CNN来提取图像特征。CNN的核心在于它的卷积核kernel，kernel是一个小窗口，在图像上平移滑动，并不断与图像进行卷积来提取窗口内的特征。这种操作的有效性在于二维图像结构的平移不变性：一个小窗口无论移动到图像的哪一个位置，其内部的结构都是一致的，因此CNN可以实现参数共享。这就是CNN的精髓所在。

针对RNN领域，它的对象是自然语言这样的序列信息，是一个一维结构，RNN就是专门针对这些序列结构而设计的，通过各种门的操作，使得序列前后的信息互相影响，从而很好地捕捉序列的特征。

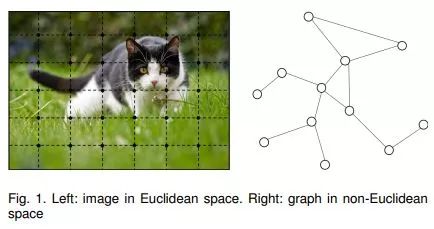
图像和自然语言，都属于欧式空间Euclidean Structure的数据，欧式空间的数据的特点就是结构很规则。但是现实生活中，其实有很多很多不规则的数据结构，典型的就是图Graph结构，或称拓扑结构，如社交网络、化学分子结构、知识图谱等等；即使是语言，实际上其内部也是复杂的树形结构，也是一种图结构；而像图片，在做目标识别的时候，我们关注的实际上只是二维图片上的部分关键点，这些点组成的也是一个图的结构。

图的结构一般来说是十分不规则的，每一个节点的度不尽相同，所以它没有平移不变性，导致传统的CNN、RNN瞬间失效。所以很多学者从上个世纪就开始研究怎么处理这类数据了。这里涌现出了很多方法，例如GNN、DeepWalk、node2vec等等。

图神经网络GNN的根本目标就是学习图中每个节点v的表示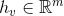，可以认为是提取每个节点的最终特征。每个节点的表示是根据当前节点特征和其邻居节点特征进行更新，这和CNN具有相同的本质。最简单的图结构是由节点和无向边构成，而实际上会分为有向图、异构图（不同类型的节点）和带边信息的图结构（不同权重或类型的边），如下图所示。综上所述，图神经网络需要解决的难点就是如何根据相邻节点特征和边的信息对当前节点特征进行更新！

最终的节点特征能够让我们可以去对图数据进行节点分类（node classification）、图分类（graph classification）、边预测（link prediction），还可以得到图的嵌入表示（graph embedding），用途非常广泛。

其实，针对Euclidean Structure数据，同样可以使用GNN，广义上来讲任何数据在赋范空间内都可以建立拓扑关联，谱聚类就是应用了这样的思想。

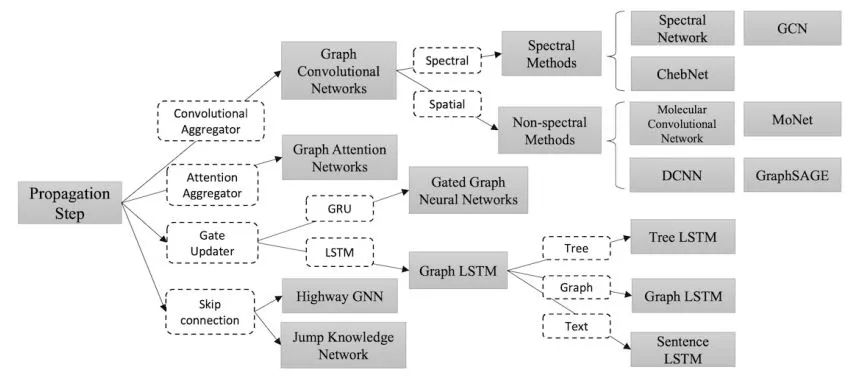
GNN根据传播方式也可以分为以下几类：图卷积神经网络GCN（Graph Convolution Networks）、基于注意力更新的图网络GAT(Graph Attention Networks)、基于门控的图网络（Gate Updater）、具有跳边的图网络（skip connection）。下文对这几种图神经网络进行概述。

GCN

GCN的本质目的就是用来提取拓扑图的空间特征，spectral domain就是GCN的理论基础了。这种思路就是希望借助图谱的理论来实现拓扑图上的卷积操作。Spectral graph theory简单的概括就是借助于图的拉普拉斯矩阵的特征值和特征向量来研究图的性质。

背景知识

(1) 拉普拉斯矩阵

对于一个图Graph，其拉普拉斯（Laplacian）矩阵的定义如下：

其中，D：Degree matrix 图中节点的度矩阵（对角矩阵，对角线上元素为各节点的度）

A：Adjacency matrix 图的邻接矩阵，反映图中每个节点之间边的特性。可见下图进行理解。

为了避免神经网络反向传播过程中的梯度消失，一般会使用归一化拉普拉斯矩阵（Symmetric normalized Laplacian）：

GCN的核心是根据拉普拉斯矩阵的特征值和特征向量来研究图的性质，所以需要进一步对拉普拉斯矩阵进行特征分解。

拉普拉斯矩阵是半正定对称矩阵，具有以下三个属性：

（1）对称矩阵一定n个线性无关的特征向量

（2）半正定矩阵的特征值一定非负

（3）对阵矩阵的特征向量相互正交，即所有特征向量构成的矩阵为正交矩阵

对拉普拉斯矩阵进行特征分解：

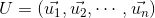
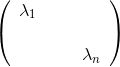
其中，：由特征向量组成的矩阵

：n个特征值构成的对角阵

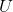
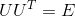
由于是正交矩阵，即，所以特征分解又可以写成：

(2）Graph傅里叶（逆）变换

为了生成Graph中的卷积操作，需要把传统的傅里叶变换以及卷积迁移到Graph上来，核心工作其实就是把拉普拉斯算子的特征函数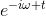变为Graph对应的拉普拉斯矩阵的特征向量。

传统傅里叶变换定义如下：

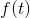
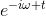
即信号与基函数乘积的积分

傅里叶变换的本质是任意一个函数可以表示为若干个正交函数（sin，cos函数）组成的线性组合，如下图所示：

而在图结构中，同理，把Graph中N维向量表示为若干个正交函数的线性组合，自然而然地想到了图拉普拉斯矩阵的特征向量。所以，仿照传统傅里叶变换，在图结构中的离散傅里叶定义如下：

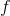
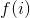
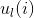
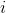
其中，是图Graph中的N维向量，与Graph的顶点一一对应

表示第个特征向量的第个分量。

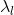
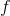
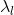
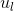
那么特征值下的，的Graph傅里叶变换就是与对应的特征向量进行内积运算。

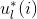
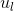
注：上述的内积运算是在复数空间中定义的，所以采用了，也就是特征向量的共轭。

进一步将Graph傅里叶变换推广为矩阵形式：

即

而针对傅里叶的逆变换，传统傅里叶逆变换是对频率进行积分：

同理，针对Graph傅里叶逆变换是对特征向量进行积分：

推广到矩阵形式如下：

即

(3）图的卷积操作

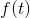
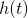
根据傅里叶变换的性质可知函数与两者的卷积是其函数傅立叶变换乘积的逆变换：

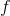
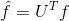
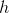
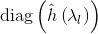
同理，针对Graph卷积，的傅里叶变换为，卷积核的傅里叶变换写成对角矩阵的形式即为，即

两者的傅立叶变换乘积即为：

再对其进行逆变换，即左乘一个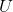，最终得到Graph中的卷积操作：

到这步，就有了对Graph进行卷积来提取特征的理论基础了。

第一代GCN

类似CNN中的卷积形式，论文Spectral Networks and Locally Connected Networks on Graphs直接将上文中的卷积项变成了卷积核再进行非线性运算，那么上文的卷积输出为

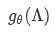
其中，

：激活函数

：GCN权重训练参数，通过初始化赋值并利用误差反向传播进行调整

：graph上对应于每个顶点的特征向量（由数据集提取特征构成的向量）

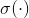
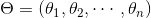
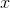
第一代GCN的存在着一些弊端：

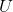
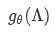
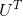
1）每一次前向传播，都要计算, 及三者的矩阵乘积，特别是对于大规模的graph，计算代价较高

2）卷积过程需要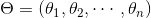n个参数，参数数量较多。

第二代GCN

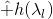
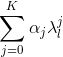
论文Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering把巧妙地设计成了，也就是：

进一步整理得

并根据以下公式：

从而导出

最终生成

其中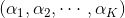是训练参数，通过初始化赋值然后利用误差反向传播进行调整。

第二代GCN设计的卷积核有如下特点：

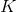
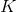
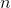
1）卷积核只有个参数，一般远小于，参数的复杂度被大大降低了

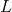
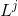
2）矩阵变换后，神奇地发现不需要做特征分解了，直接用拉普拉斯矩阵进行变换。然而由于要计算，计算复杂度还是

3）卷积核有很好的空间局部性（图论：通过计算邻接矩阵的K次方得到的矩阵非零位置表示两个节点存在长度为K的路径，K就是卷积核的receptive field，也就是说每次卷积会将节点的路径长度为K的领域节点的特征进行加权求和），可见下图分析：

注：GCN每次卷积过程对所有节点进行上图操作。

Chebyshev多项式递归计算卷积核

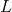
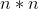
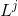
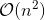
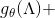
在第二代GCN中，是的矩阵，所以的计算复杂度还是，论文Wavelets on graph via special graph theory提出了利用切比雪夫Chebyshev多项式拟合上文卷积核的方法，来降低计算复杂度。卷积核可以利用截断（truncated）的shifted Chebyshev多项式来近似逼近。

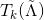
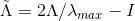
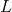
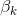
其中，：（经的最大特征值（即谱半径）缩放后的特征向量矩阵）的Chebyshev多项式，进行这个shift变换的原因是Chebyshev多项式的输入要在 [-1,1]之间

：Chebyshev多项式的系数

从而可得到：

由Chebyshev多项式的性质，已知以下递推公式

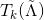
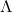
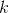
而是的阶多项式，且有

其中，

这样，就得到下述的公式：

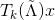
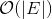
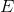
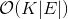
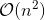
这个时候不难发现：卷积操作不再有矩阵乘积了，只需要计算矩阵与向量的乘积即可。计算一次的复杂度是，是图中边的集合，则整个运算的复杂度是。当graph是稀疏图的时候，计算加速尤为明显，这个时候复杂度远低于。

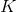
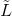
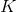
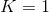
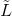
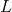
该近似的谱图卷积虽然可以建立起阶邻居的依赖，然而，却仍然需要在上进行阶运算。在实际过程中，这一运算的代价也是非常大的。为了降低运算代价，本文进一步简化了该运算，即限定。此时，谱图卷积可以近似为（或）的线性函数。

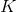
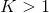
当然，这样做的代价是，只能建立起一阶邻居的依赖。对于这一问题，可以通过堆积多层图卷积网络建立阶邻居的依赖，而且，这样做的另一个优势是，在建立阶邻居的依赖时，不需要受到切比雪夫多项式的限制。

为了进一步简化运算，在GCN的线性模型中，本文定义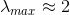。此时，我们可以得到图谱卷积的一阶线性近似：

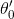
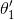
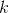
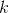
可以看到，该式中仅有两个参数与。若需建立阶邻居上的依赖，可以通过设置层这样的滤波器来实现。

在实际的过程中，可以通过对参数进行约束来避免过拟合，并进一步简化运算复杂度。例如，可以令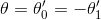，从而得到

需要注意的是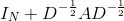，的特征值范围为[0,2]，这意味着，当不停地重复该操作时（网络非常深时），可能会引起梯度爆炸或梯度消失。为了减弱这一问题，提出了一种 renormalization trick：

其中，

只使用A的话，由于A的对角线上都是0，所以在对其进行信息提取的收，只会计算当前节点所有邻居的特征加权和，该节点自身的特征却被忽略了。因此，我们可以做一个小小的改动，给A加上一个单位矩阵，这样就让对角线元素变成1了，形成一个自环！

当图中每个节点的表示不是单独的标量而是一个大小为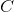的向量时，可以使用其变体进行处理：

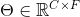
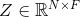
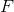
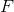
其中，表示参数矩阵，为相应的卷积结果。N为图中节点个数，C为每个节点的特征向量维度，F是变换后每个节点特征向量的维度，此时，每个节点的节点表示被更新成了一个新的维向量，该维向量包含了相应的一阶邻居上的信息。

经过以上的推导，本文得到了图卷积神经网络的（单层）最终形式

其中，第层网络的输入为（初始输入为）

为图中的节点数量，每个节点使用维的特征向量进行表示

为添加了自连接的邻接矩阵

为度矩阵，

为待训练的参数

为相应的激活函数，例如。

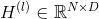
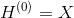
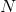
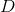
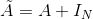
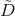
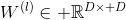
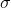
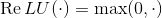
训练过程中，输入图结构，经过GCN特征提取，输出每个节点最终表示，计算有标签的节点的训练损失，进行反向传播误差进行梯度下降算法来调整权重参数，可实现半监督分类。

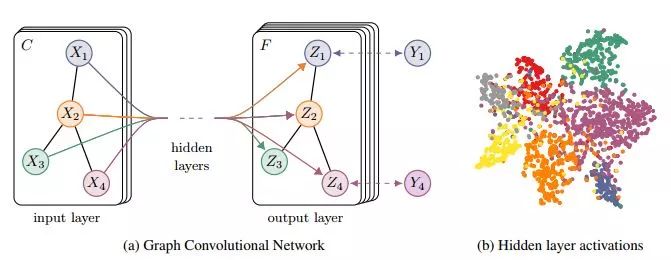
Semi-Supervised Classification with Graph Convolutional Networks

github地址

基于谱的方法需要学习的参数都是与Laplacian矩阵的特征向量和特征值相关的，即取决于图的结构，这样有什么问题呢，如果你在一个大图或者很多同构的小图上进行训练是可以的，这也有很多应用场景。但是如果我们要处理很多不同结构的图，那就不能用同一套参数来学习，不惧泛化性，比如我们对很多树结构的句子进行分类（句子表示为依存句法树或其他），每个句子的表示可能都不同，那就没办法用上面的方法做。

DeepSEA

Convolutional Networks on Graphs for Learning Molecular Fingerprints

github地址

DeepSEA

为了对图中每个节点特征进行更新，DeepSEA使用最简单的算法，即根据邻接矩阵获取当前节点的邻居节点，再把对其邻居节点特征进行直接求和，以实现对当前节点特征的更新，更新公式如下所示：

其中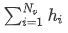，：邻居节点表示的向量和

第一个公式为收集和整合当前节点的邻居节点特征

第二个公式为对当前节点特征进行更新。

DCNN

Diffusion-Convolutional Neural Networks

github地址

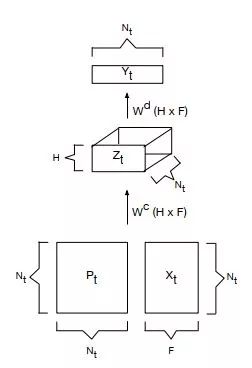
为了对图中每个节点进行分类，需对每个节点特征进行更新，DCNN提出的更新公式如下：

其中，

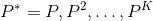
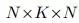
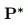
, P是通过将邻接矩阵中每一行除以该行节点的度计算得到的度归一化邻接矩阵，是一个N×N张量，而是将（K×N×N的张量）经过维度变换生成的张量，N是图中节点个数

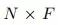
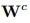
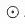
X：图中所有节点的特征矩阵，是张量，F为每个节点特征的长度

：是一个维度为K×F的权重参数

：点乘

Z ：维度为N×K×F的节点表示

f（）：一个非线性函数

获取了每个节点表示，为了进一步对节点进行分类，再对Z进行全连接操作，生成N×C的张量，最后使用softmax。公式如下：

针对节点分类，整个算法流程可用下图表示：

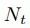
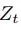
注：图中就是上文的N，H就是上文的K，就是上文的Z。

GraphSAGE

Inductive Representation Learning on Large Graphs

github地址

GraphSAGE框架的核心是如何聚合节点邻居特征信息来对当前节点特征进行更新，下文介绍GraphSAGE前向传播过程（生成节点embedding）和不同的聚合函数设定。

1. 前向传播

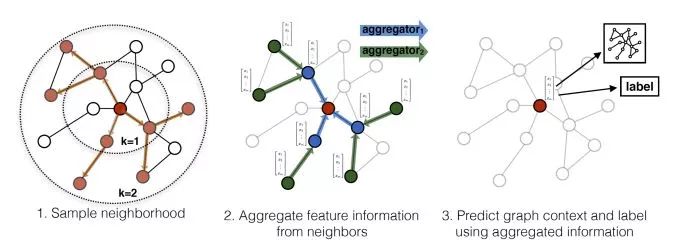
下图是GraphSAGE 生成目标节点（红色）embededing并供下游任务预测的过程：

（1）先对邻居随机采样，降低计算复杂度（图中一跳邻居采样数=3，二跳邻居采样数=5）

（2）生成目标节点emebedding：先聚合二跳邻居特征，生成一跳邻居embedding，再聚合一跳邻居embedding，生成目标节点embedding，从而间接获得二跳邻居信息。

（3）将embedding作为全连接层的输入，预测目标节点的标签。

前向传播伪代码如下：

2. 聚合函数

每个节点需要获取邻居节点的特征信息，这个过程叫做聚合过程。聚合过程可以使用不同聚合函数，本小节介绍五种满足排序不变量的聚合函数：平均、GCN归纳式、LSTM、pooling聚合器。（因为邻居没有顺序，聚合函数需要满足排序不变量的特性，即输入顺序不会影响函数结果）

a.平均聚合：先对邻居embedding中每个维度取平均，然后与目标节点embedding拼接后进行非线性转换。

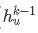
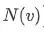
其中，：当前节点v的邻居节点上一层的embedding

: 当前节点v的邻居节点

b. 归纳式聚合：直接对目标节点和所有邻居emebdding中每个维度取平均（替换伪代码中第5、6行），后再非线性转换：

c. LSTM聚合：LSTM函数不符合“排序不变量”的性质，需要先对邻居随机排序，然后将随机的邻居序列embedding 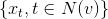作为LSTM输入。

d. Pooling聚合器: 先对每个邻居节点上一层embedding进行非线性转换（等价单个全连接层，每一维度代表在某方面的表示（如信用情况）），再按维度应用 max/mean pooling，捕获邻居集上在某方面的突出的／综合的表现以此表示目标节点embedding。

对于上述所有的聚合方法，可以使用以下统一公式进行概括：

这里的AGGREGATE可以指上文中不同的聚合函数。

GAT

GRAPH ATTENTION NETWORKS

github地址

图的节点之间的信息传递当然也可以用attention进行控制（NLP中的每个单词、CV中的每个像素当做一个节点，它们的attention都可以当做是在图上的操作），通过当前节点的不同邻居与当前节点的关系计算信息流的权重, Graph Attention Network (GAT) 提出了用注意力机制对邻居节点特征加权求和。邻居节点特征的权重完全取决于节点特征，独立于图结构。

图注意力模型 GAT 用注意力机制替代了GCN中固定的标准化操作。以下公式定义了如何对第 l 层节点特征做更新得到第 l+1 层节点特征：

其中，

第一个等式表示对节点特征表示进行线性变换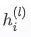（为第l层中图第i个节点的特征嵌入）

第二个等式计算了成对节点间的原始注意力分数。它首先拼接了两个节点的特征嵌入Z（ || 在这里表示拼接concatenate）；随后对拼接好的嵌入以及一个可学习的权重向量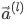做点积；最后应用了一个 LeakyReLU 激活函数。

第三个等式公式对一个节点所有入边的原始注意力分数应用了一个 softmax 操作，得到了注意力权重

第四个等式形似 GCN 的节点特征更新规则，对所有邻节点的特征做了基于注意力的加权求和

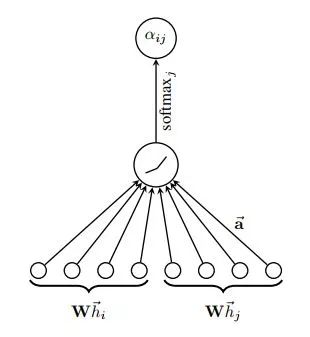
上述节点特征嵌入可用如下示意图进行表示：

GGNN

PPT

GATED GRAPH SEQUENCE NEURAL NETWORKS

github地址

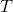
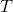
相比于GNN，GGNN的特点在于使用了门控单元来控制信息的传播，比如可以用GRU，LSTM等门控方式来传递图的信息而且，节点表示的更新次数被固定成了。也就是说，GGNN并不能保证图的最终状态会到达不动点。由于更新次数变成了固定值，因此GGNN可以直接使用BPTT算法来进行梯度的计算。

1.传播过程

这里只介绍一下基于GRU的GGNN，传播过程可以表示为：

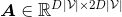
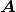
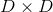
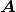
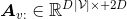
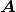
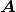
其中，表示图中节点与其他节点的连接关系（可以视作将邻接矩阵的每一个“1”元素替换为的传播矩阵得到），在大多数情况下，是比较稀疏的矩阵，而且，在同一类型的边上，参数是共享的

是的一个子矩阵，对应于中与节点有关的列。

|V|是节点个数

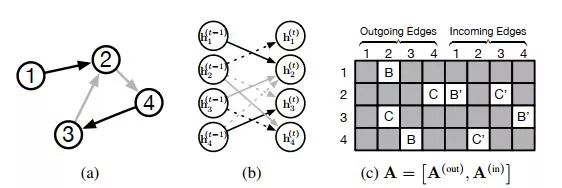
D是表示一个节点所需的维度，2D|V|中的2是因为边有两种类型，如下图（c）所示。

第一个等式是一个初始化步骤，用于将节点特征复制到节点状态向量中，其余部分使用0补齐。

第二个等式用于不同节点之间的信息传播，这些信息传播要受到图中边的限制(包括是否有边、边的方向以及边的类型)。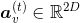包含了每个方向上的激活。

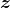
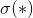
其余等式就是GRU单元。与分别表示更新门与重置门，为sigmoid函数，表示逐元素相乘

2.输出过程

根据任务的不同，GGNN可以有多种不同形式的输出。

当GGNN用于node-focused任务时，对于每个节点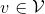都需要有一个输出：

若对于图级(graph-level)输出，可以定义一个图的表示向量：

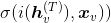
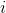
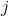
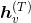
其中，相当于一个soft attention机制，用于决定哪个节点与当前的任务有关。与都是神经网络，其输入是与的连接，输出是实值向量。tanh函数也可以被替换为恒等变换。

Skip connection

Semi-supervised User Geolocation via Graph Convolutional Networks

github地址

相比于传统的网络，GNN的深度一般更浅，原因是随着深度的增加，梯度消失很明显，以及GNN的感受野指数增大在信息传递过程中会引入大量噪声。所以在GNN中也有人尝试加入skip connection来缓解这个问题。下面是一个用Highway门控的方法的例子：

其中，

第一个公式计算Highway的权重，用于控制层输入信息对当前层的影响

第二个公式根据Highway权重综合计算层的输入和输出的门控权重和来获取最终节点特征嵌入

参考资料

(1) [Graph Neural Networks （GNN）综述简介]

(https://zhuanlan.zhihu.com/p/68015756)

(2) [如何理解 Graph Convolutional Network（GCN）？]

(https://www.zhihu.com/question/54504471/answer/332657604)

(3) [图卷积神经网络(GCN)详解:包括了数学基础(傅里叶，拉普拉斯)](https://zhuanlan.zhihu.com/p/67522582)

(4) [Gated Graph Sequence Neural Networks]

(https://arxiv.org/abs/1511.05493)

(5) [Graph Attention Networks](https://arxiv.org/abs/1710.10903)

(6) [深入理解图注意力机制](https://zhuanlan.zhihu.com/p/57180498)

(7)[如何理解 Graph Convolutional Network（GCN）？]

(https://www.zhihu.com/question/54504471/answer/730625049)

交流群

欢迎加入公众号读者群一起和同行交流，目前有SLAM、算法竞赛、图像检测分割、人脸人体、医学影像、自动驾驶、综合等微信群（以后会逐渐细分），请扫描下面微信号加群，备注：”昵称+学校/公司+研究方向“，例如：”张三 + 上海交大 + 视觉SLAM“。请按照格式备注，否则不予通过。添加成功后会根据研究方向邀请进入相关微信群。请勿在群内发送广告，否则会请出群，谢谢理解~