使用卡尔曼滤波器和路标实现机器人定位

2019 年 2 月 26 日 AI研习社

本文为 AI 研习社编译的技术博客，原标题：

Robot localization with Kalman-Filters and landmarks

作者 | Jannik Zürn

翻译 | 郭乃峤、ThomasGui

校对 | Disillusion 审核 | 酱番梨整理 | 立鱼王

原文链接：

https://medium.com/@jannik.zuern/robot-localization-with-kalman-filters-and-landmarks-cf97fa44e80b

注：本文的相关链接请访问文末二维码

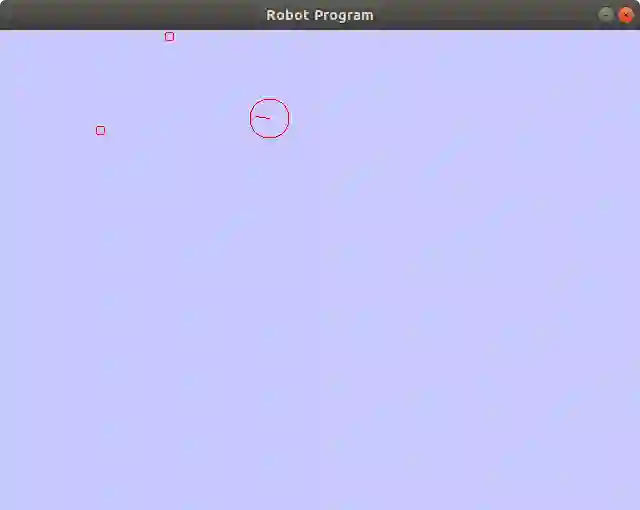
让我来介绍一下——Robby 是个机器人。技术上说他是个过于简单的机器人虚拟模型，但对我们的目的来说足够了。Robby 迷失在它的虚拟世界，这个世界由一个2维平面构成，里面有许多地标。他有一张周围环境的地图（其实不需要地图也行），但是他不知道他在环境中的确切位置。

Robby(红色大圆圈)和2个地标（红色小圆圈）

这个文章的目的是教你用地标检测和扩展卡尔曼滤波器一步一步实现机器人定位。

第一部分-线性卡尔曼滤波器

卡尔曼滤波器可以理解为一种感知充满噪声的世界的方式。当我们要定位机器人在哪里，依赖两个条件：我们知道机器人如何从一个时刻移动到下个时刻，因为我们以某种确定的方式命令它移动。这称为状态转移（即机器人如何从一个状态转移到另一个）而且我们能用各种传感器如相机，激光雷达或回波探测器（德语：毫米波雷达）测量机器人的环境。问题是这2类信息都受到噪声影响。我们不能精确地知道机器人从一个状态转移到下一个状态的精确程度，因为执行部件不完美。而且我们不能无限精确地测量物体间的距离。这就是卡尔曼滤波器发挥作用的场合。

卡尔曼滤波器允许我们结合当前状态的不确定和它的传感器测量的不确定来理想地降低机器人的总体不确定程度。这两类不确定通常用高斯概率分布或正态分布来描述。高斯分布有2个参数：均值和方差。均值表示最高概率的值，方差表示我们认为这个均值有多大的不确定性。

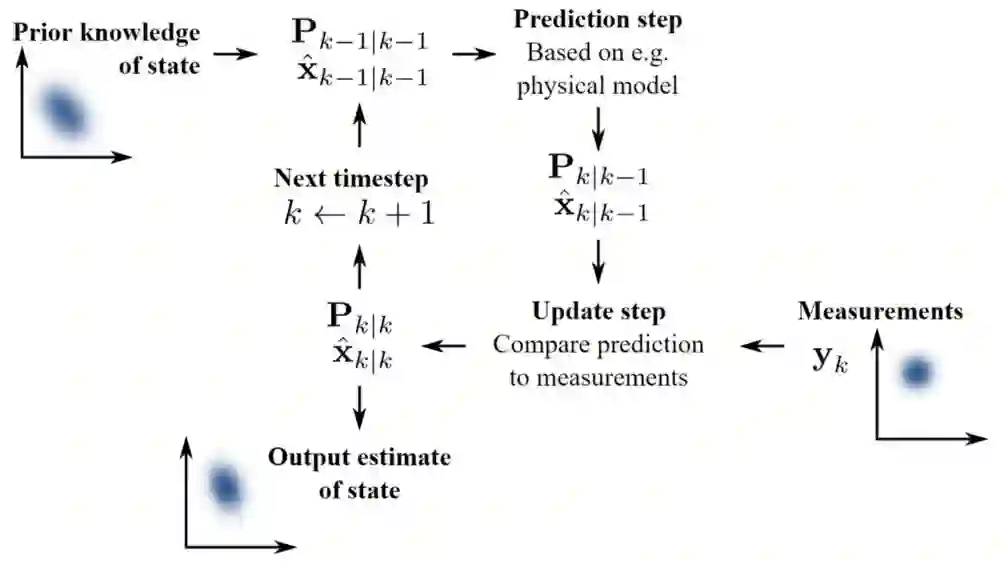
卡尔曼滤波器运行2个步骤。在预测步骤，卡尔曼滤波器以当前状态变量值生成预测和不确定度。当观测到下一次测量结果（必然有一定的误差，包含噪声），就能以加权平均的方式更新这些预测，确定程度高的预测给予更高的权重。算法是递归的。它可以实时运行，仅需要当前测量输入和前个计算的状态和不确定矩阵；不需要更多的过去信息。

因为Wikipedia 关于卡尔曼滤波器的信息流图太好了，我这里就直接用它了：

卡尔曼滤波器图片来自：https://upload.wikimedia.org/wikipedia/commons/a/a5/Basic_concept_of_Kalman_filtering.svg

我不会深入探讨卡尔曼滤波器的数学计算细节，因为很多聪明人已经做过了。如想要了解更深层次的解释，我可以推荐Tim Babb的博客：

How a Kalman filter works, in picturesI have to tell you about the Kalman filter, because what it does is pretty damn amazing. Surprisingly few software…

第二部分-扩展卡尔曼滤波器

扩展卡尔曼滤波器（如名字所示）是“标准”卡尔曼滤波器的扩展。在上节内容我没有告诉你的一个隐含的假设：当使用卡尔曼滤波器时，状态转移和测量必须是线性模型。从数学观点，这意味着我们可以采用这个假设和线性代数的优雅来更新机器人状态和机器人测量。实际上，这意味着状态变量和测量值随着时间线性改变。举个例子，如果我们测量机器人的X 方向位置。我们假设机器人在时刻t1 位于x1, 它在t2时刻必定位于x2位置。变量v表示机器人在x 方向的速度。假设机器人实际上在加速，或任意非线性运动（例如沿着圆周运动），状态转移模型有点错误。在大多数情形下，并没有多大的错误。但是在某些边界情形，这个线性假设就错的离谱。

同样假设线性测量模型也会有问题。假设你正沿着直路行驶，在你前方的路旁有一个灯塔。而你离的比较远，你测量到离灯塔的距离和它位于你视野的角度接近线性地改变（距离大致以你的车辆的速度来减少，而且角度基本不变）。但是当你越来越靠近，尤其当你行驶过它的时候，角度则急剧地改变。这就是为什么当Robby在它的2-D 世界采用散落在它的2-D 平面的地标导航的时候，我不能再用线性卡尔曼滤波器。

扩展卡尔曼滤波器是拯救者，它解除了线性状态转移和测量模型的线性限制。而它允许使用任何非线性函数对你的机器人状态转移和测量建模。为了还能在我们的滤波器中使用有效而且简单的线性代数的魔力，我们采取了一个技巧：我们在当前机器人状态邻域采取线性化。这意味着我们假设测量模型和状态转移模型在我们当前的状态附近接近线性（再次引用路/灯塔的例子）。但在每个步骤之后，我们在新状态的临域线性化更新。而这个方法迫使我们对非线性函数采取线性化。

这就是结果。扩展卡尔曼滤波基本上是“正常”卡尔曼滤波，只是对现有的非线性状态转移模型和测量模型进行了额外的线性化。

在我们的例子中，Robby迷路了，想要在这个(有争议的)敌对环境中进行本地化，扩展卡尔曼滤波使Robby能够感知地标并相应地更新其状态信念。如果状态估计值和测量估计值的方差足够低，罗比很快就能非常确定他所处的位置相对于地标的位置因为他知道地标的确切位置，他知道自己在哪里!

他的快乐指数飙升!

第三部分-实现

实现的代码是非常直接的。为了直观，我选择使用SDL2 库去实现一些必要物体的图像。这里可以下载：

根据面向对象编程，我实现了下面的类：

Robert类

这个类最重要的部分是Pose(x 的位置, y的位置, 方向) 和 Velocity (线速度和角速度)。它可以向前，向后，向右和想左旋转。为了测量路标的位置，它有measureLandmarks方法，这个方法可以获取真实的路标，并且考虑路标的位置和观测噪音，从而得到观测过的路标的列表。

class Robot {
public:
    Robot(int x_start, int y_start, float orientation, int radius, SDL_Color col);
    ~Robot();
    
    void render(SDL_Renderer * ren);
    void move(const Uint8 * , Eigen::VectorXf & control);
    void moveForward(Eigen::VectorXf & control);
    void moveBackward(Eigen::VectorXf & control);
    void rotateLeft(Eigen::VectorXf & control);
    void rotateRight(Eigen::VectorXf & control);
    void setPose(float x, float y, float phi);

    Eigen::VectorXf get_state();
    std::vector<Landmark> measureLandmarks(std::vector<Landmark> landmarks);

private:
    Pose pose;
    Velocity velocity;
    SDL_Color color;
    int radius;
};

KalmanFilter类

这个类毫无疑问非常复杂。他的成员是矩阵。矩阵可以用来状态转换，观测，计算协方差。我会掠过大部分细节，因为代码注释已经提供了提示关于代码的目的。过滤在localization_landmarks函数里实现。

class KalmanFilter {
public:


    /**
    * Create a Kalman filter with the specified matrices.
    *   A - System dynamics matrix
    *   C - Output matrix
    *   Q - Process noise covariance
    *   R - Measurement noise covariance
    *   covariance - Estimate error covariance
    */

    KalmanFilter(
            double dt,
            const Eigen::MatrixXf& A,
            const Eigen::MatrixXf& C,
            const Eigen::MatrixXf& Q,
            const Eigen::MatrixXf& R,
            const Eigen::MatrixXf& covariance
    );

    /**
    * Initialize the filter with a guess for initial states.
    */
    void init(double t0, const Eigen::VectorXf& x0);

    /**
    * Update the estimated state based on measured values. The
    * time step is assumed to remain constant.
    */
    void update(const Eigen::VectorXf& y);

    /**
    * Return the current state and time.
    */
    Eigen::VectorXf get_state() { return state; };

    void renderSamples(SDL_Renderer * ren);

    void localization_landmarks(const std::vector<Landmark> & observed_landmarks,
                                const std::vector<Landmark> & true_landmarks,
                                const Eigen::VectorXf & control);

private:

    // Matrices for computation
    Eigen::MatrixXf A, C, Q, R, covariance, K, P0;

    // System dimensions
    int m, n;

    // Initial and current time
    double t0, t;

    // Discrete time step
    double dt;

    // Is the filter initialized?
    bool initialized;

    // n-size identity
    Eigen::MatrixXf I;

    // Estimated states
    Eigen::VectorXf state, state_new;
};

Landmark类

这个类是最简单的。他有位置，ID, 一个把自己呈现在屏幕上的方法。这就是全部了。

class Landmark {
public:
    Landmark(float x, float y, SDL_Color id);
    ~Landmark();
    Position pos;
    SDL_Color id;
    void render(SDL_Renderer * ren);
};