【元图(Meta-Graph)：元学习小样本连接预测】

这篇文章是基于这篇论文“Meta-Graph: Few Shot Link Prediction via Meta Learning” by Joey Bose, Ankit Jain, Piero Molino, and William L. Hamilton.

许多真实世界的数据都是以图的结构呈现，因此，多年来基于图的机器学习研究一直是学术界研究的一个活跃领域。其中，一个流行基于图数据的机器学习的任务是链接预测，它涉及到预测图数据中节点之间缺失的关系/边。例如，在一个社交网络中，我们可能使用链接预测来支撑一个朋友推荐系统，或者在生物网络数据中，我们可能使用链接预测来推断药物、蛋白质和疾病之间可能的关系。然而，尽管链接预测很受欢迎，但是以前的工作通常只关注一个特定的问题设置:它通常假设链接预测是在一个大型图上执行的，并且这个图是相对完整的，即在训练过程中，至少有50%的真实边是可以观察到的。

在这项工作中，我们考虑了更有挑战性的小样本链接预测设置，其中的目标是对多个图执行链接预测，这些图只包含它们的真实、底层边的一小部分。这个任务的灵感来自于这样的应用程序:我们可以访问来自单个域的多个图，但是每个单独的图只包含真实的底层边的一小部分。例如，在生物环境中，高通量互作提供了从不同的组织、细胞类型和生物体估计数以千计的生物互作网络的可能性；然而，这些估计的关系可能是有噪音的和稀疏的，我们需要学习算法来利用这些多个图的信息来克服这种稀疏性。类似地，在电子商务和社交网络设置中，当我们必须快速地对稀疏估计的图进行预测时，比如最近将某个服务部署到新地区时，链接预测通常会产生很大的影响。换句话说，新的稀疏图的链接预测可以受益于从其他图(可能更密集的图)传输知识，假设存在可利用的共享结构。

我们介绍了一个新的框架元图，用于小样本链接预测，和以及相应的一系列基准测试。我们采用了经典的基于梯度的元学习公式对图域进行小样本分类。具体地说，我们把图上的分布看作是学习全局参数集的任务上的分布，并将此策略应用于训练能够进行小概率链路预测的图神经网络(GNNs)。为了进一步引导快速适应新图，我们还引入了图签名函数，该函数学习如何将输入图的结构映射到GNN链路预测模型的有效初始化点。我们在三个链接预测基准上对我们的方法进行了实验验证。我们发现我们的MetaGraph方法不仅实现了快速适应，而且在许多实验设置中收敛到更好的整体解决方案，在非元学习基线上收敛的AUC平均提高了5.3%。

小样本链接预测设置

给定一个分布在图p(G)上的分布，从中我们可以对一个训练图Gi = (Vi, Ei, Xi)进行抽样，其中Vi是节点集合，Ei是边集合，Xi是一个实值节点属性矩阵。我们假设每个示例图Gi都是一个简单的图，这意味着它只包含一种类型的关系，没有自环。我们进一步假设，对于每个图Gi，我们在训练期间只能访问少量的训练边E_train (其中|E_train| << |E|)。最后，我们假设p(G)是在一组相关图上定义的，不管它们是来自一个公共域还是具体的应用设置。

我们的目标是学习一个全局或元链接预测模型的样本训练图表Gi~p (G) （其中i=1,2...n）。有了这个元模型，随后我们可以快速学习局部链接预测模型从边的一个小子集内新采样图G*~p (G)。更具体地说，我们想找一个全局的参数θ，它可以在局部链接预测模型图G生成一个有效的参数初始化φ。

请注意，这与标准的链接预测设置有很大的不同，后者的目标是从单个图而不是图的分布中学习。它也不同于用于小样本分类的标准元学习，后者通常假设任务中个体预测是独立且同分布的，而与训练图中相互依赖的边相反。

方法：元图

我们的方法，元图，利用了图神经网络(GNNs)。原则上，它可以与多种基于GNNs的链路预测方法相结合，但我们采用了一种特定的GNN——变分图自动编码器(VGAEs)作为我们的基本链路预测框架。

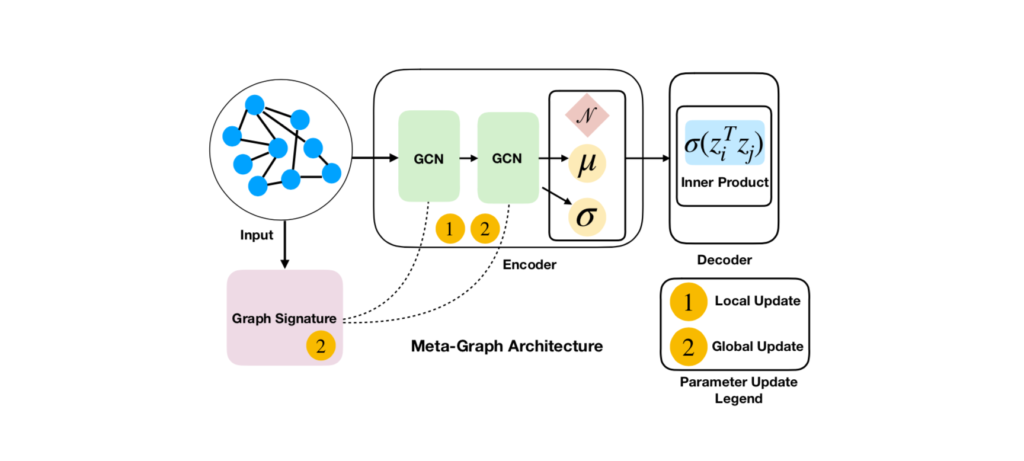
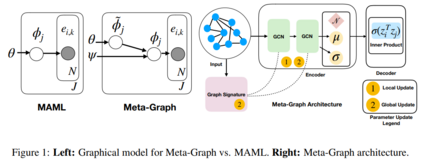
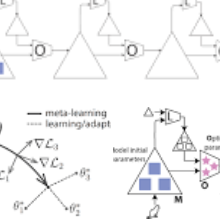
Meta-Graph背后的关键思想是基于我们使用梯度元学习优化共享全局参数θ,用于初始化VGAE链接预测模型的参数。同时，该模型还学习了一个图签名函数，这是一个图的向量表示，我们使用它来调整VGAE模型的参数。如果模型观察到的图与当前正在检查的图相似，它就能够相应地调整模型参数。这有助于模型利用梯度下降的几个步骤来学习有效的参数。

如果我们给出一个采样的训练图Gi，我们使用两个学习组件的组合初始化VGAE链接预测模型的参数：

• 全局参数θ,用于初始化VGAE模型所有的参数φ。φ参数优化的梯度下降的n步，尽管全局参数θ，通过二阶梯度下降优化提供一个有效的初始化点的任何图采样分布p(G)。
• 图签名si =ψ(Gi),用于调节VGAE的激活模式。通过另一个GNN获得图的签名函数。像全局参数θ，类似地，图签名模型ψ是通过二阶梯度下降优化编码相似参数初始化的本地链接预测模型图元学习的目的。关于我们的图签名函数的更多信息，请参考我们的论文。

总的来说，训练的算法可以总结如下：

• 采样一批训练图
• 使用全局参数和签名函数初始化这些训练图的VGAE链接预测模型
• 运行k个梯度下降步骤来优化这些VGAE模型
• 使用二阶梯度下降更新全局参数和基于边验证集的签名函数

我们的论文详细介绍了元图的其他几个变体，它们在如何使用图形签名函数的输出来调节VGAE推理模型的激活方面有所不同。

实验

为了测试元图在真实环境中的工作方式，我们设计了三个新的基准来进行小样本链接预测。所有这些基准测试都包含一组从公共域绘制的图。在所有设置中，我们使用这些图的80%作为训练图，10%作为验证图，其中这些训练图和验证图用于优化全局模型参数(用于元图)或训练前权重(用于各种基线方法)。剩下的10%作为测试图，我们的目标是在这些测试图上训练一个模型，以达到较高的链接预测精度。

在这个小样本链接预测设置中，在边层和图层都有训练/验证/测试分割。我们使用训练边在每个图的基础上预测测试边的可能性，但我们也同时在多个图上对模型进行训练，目的是通过全局模型参数快速适应新的图。

我们的两个基准来自于蛋白质相互作用(PPI)网络和3D点云数据(FirstMM-DB)的标准多图数据集。第三种是基于AMINER引用数据的新型多图数据集，其中每个节点对应一篇论文，链接代表引用。对于所有数据集，我们通过对一个小子集(即，然后尝试预测不可见的边(20%的剩余边用于验证)。

一些基线对应于元图的修改或消融，包括模型无关元学习(MAML)的直接适应，一个微调的基线，在这里我们对VGAE按顺序观察的训练图进行预训练，并对测试图进行调优（称为 Finetune）。我们还考虑在每个测试图上单独训练一个VGAE(称为No Finetune)。我们为链接预测任务使用了另外两个标准基线，即DeepWalk和Adamic-Adar来进行比较，以确保元图能够提供实质性的改进。

结果

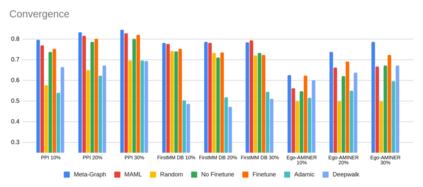
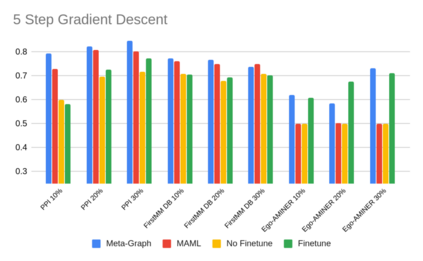
我们比较了元图和基线模型在两种情况下的表现，以了解模型适应新的不可见测试图的能力和速度。收敛设置，我们训练模型收敛，和快速适应设置，我们适应模型后，只执行5个梯度更新。在这两种设置中，我们使用测试图的10%、20%和30%的边进行训练，并对测试图的测试边进行测试。我们通过计算链路预测AUC来衡量性能。

对于收敛设置。我们发现Meta-Graph获得了最高的平均AUC，与MAML方法相比，相对改善了4.8%，与Finetune基线相比，相对改善了5.3%。当只使用10%的边时，元图的性能更强，这表明在处理非常有限的数据时该方法的潜力。

在快速适应设置中，我们再次发现Meta-Graph在除一个设置外的所有设置中都优于所有基线，与MAML相比平均相对改进9.4%，与Finetune基线相比平均相对改进8%。换句话说，元图不仅可以从有限的数据中学习，还可以快速地接收新数据，只需要很少的梯度步骤。

展望

在本研究中，我们引入了元图(Meta-Graph)，这是一种解决小样本链路预测问题的方法，其目标是精确地训练ML模型，使其能够快速适应新的稀疏图数据。在实验上，我们观察到使用元图与在三个小样本链接预测变体基准上的基线相比，有显著的提高。

总的来说，这项工作适用于研究人员从一个域访问多个图，但其中每个单独的图只包含真实的底层边的一小部分。例如，在生物环境中，高通量互作提供了从不同的组织、细胞类型和生物体估计数以千计的生物互作网络的可能性;然而，这些估计的关系可能是嘈杂的和稀疏的，我们需要学习算法来利用这些多个图的信息来克服这种稀疏性。类似地，正如前面提到的，在电子商务和社交网络设置中，当我们必须快速地对稀疏估计的图进行预测时，比如最近将某个服务部署到新地区时，链接预测通常会产生很大的影响。换句话说，新的稀疏图的链接预测可以受益于从其他图(可能更密集的图)传输知识，假设存在可利用的共享结构。