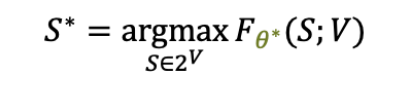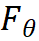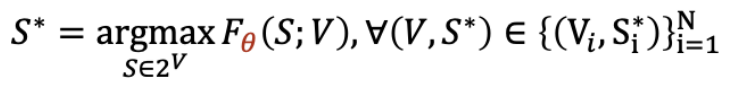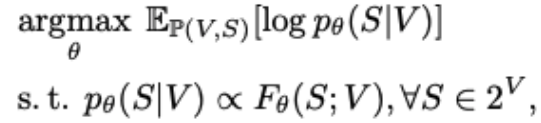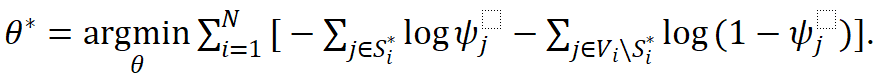NeurIPS 2022 Oral | 基于最优子集的神经集合函数学习方法EquiVSet
机器之心专栏
腾讯 AI Lab、帝国理工与中山大学合作发表论文《Learning Neural Set Functions Under the Optimal Subset Oracle》,提出基于最优子集的集合函数学习方法。
集合函数被广泛应用于各种场景之中,例如商品推荐、异常检测和分子筛选等。在这些场景中,集合函数可以被视为一个评分函数:其将一个集合作为输入并输出该集合的分数。我们希望从给定的集合中选取出得分最高的子集。鉴于集合函数的广泛应用,如何学习一个适用的集合函数是解决许多问题的关键。为此,腾讯 AI Lab、帝国理工与中山大学合作发表论文《Learning Neural Set Functions Under the Optimal Subset Oracle》,提出基于最优子集的集合函数学习方法。该方法在多个应用场景中取得良好效果。论文已被 NeurIPS 2022 接收并选为口头报告(Oral Presentation)。
论文地址:https://arxiv.org/abs/2203.01693
代码地址:https://github.com/SubsetSelection/EquiVSet
一、引言
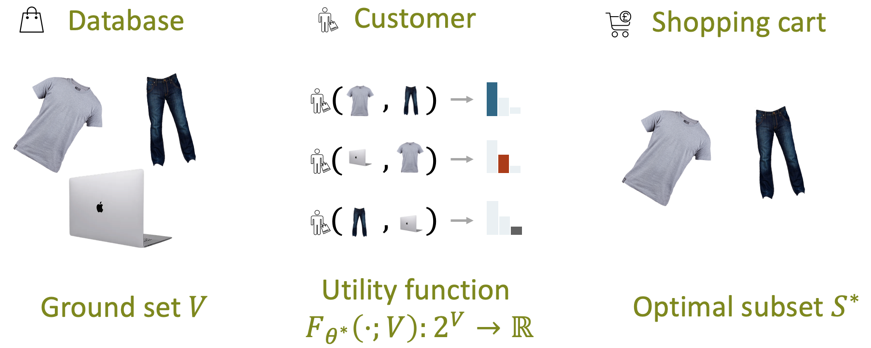
很多现实应用场景与集合密切相关,例如推荐系统、异常检测和分子筛选等。这些应用都潜在地学习了一个集合函数来评价给定集合的得分,使得输出的集合拥有最高得分。以商品推荐为例子(如下图所示),我们希望从某个网店的商品库V中推荐子集,使得用户对该商品子集拥有最高评分
图 1 集合函数学习在商品推荐中的例子
具体地,我们假设每个用户心中存在一个评分函数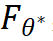
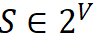
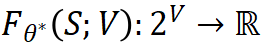
我们希望学习一个函数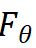
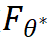
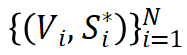
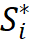
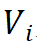
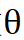
然而找到合适的参数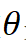
其中我们通过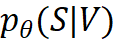
在本文中,我们提出了等变变分集合函数学习方法 (Equivariant Variational inference for Set function learning. EquiVSet). 具体地,我们使用能量模型(energy-based models)建模概率
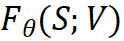
二、方法简介
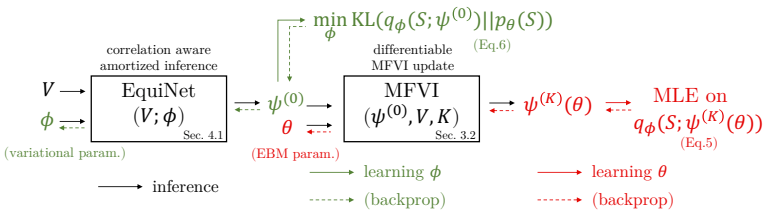
图 2 EquiVSet 训练和推理过程概览
我们首先将概率模型定义为能量模型: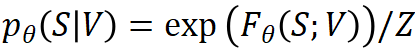
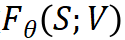
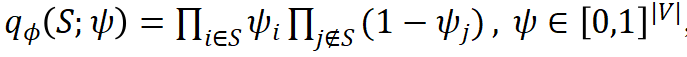
1. 为了学习变分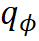
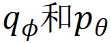
2. 为了训练模型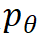
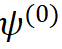
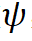
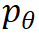
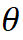
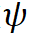
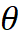
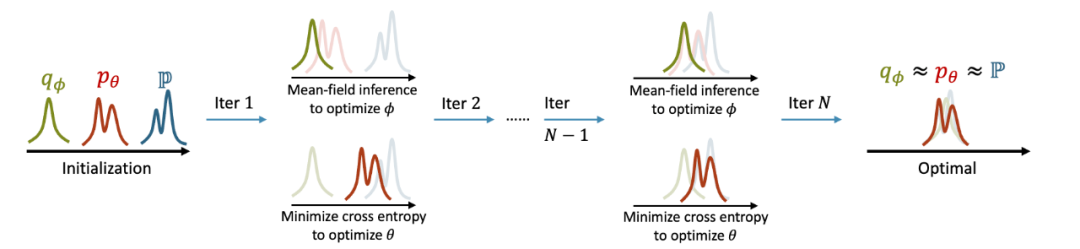
模型通过反复迭代步骤 1 和 2 来更新参数, 从而达到合作式训练变分网络 EquiNet 和能量网络的目的。这种合作学习方式的效果可以通过图 3 形象示意:在每轮迭代中,我们通过均摊变分推断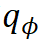
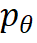
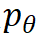
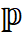
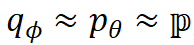
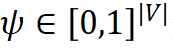
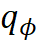
图 3 EquiVSet 参数更新示意图
三、实验结果
为了验证 EquiVSet 的有效性,我们在三个任务上进行测试:商品推荐、异常检测和分子筛选。
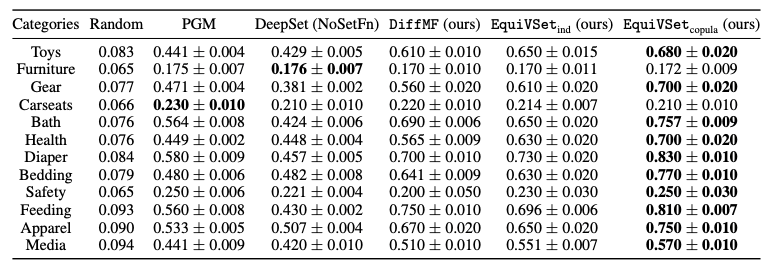
1. 在商品推荐任务中,我们使用 amazon baby register dataset,该数据集包含了真实的用户购买记录。在该任务上,EquiVSet 在大部分场景中都取得最佳性能。具体地,相比于先前的 SOTA 算法 PGM,EuiVSet 的性能平均提升 33%。相比于传统的黑盒端到端子集预测方法 DeepSet(NoSetFn)(该方法相当于仅建模了变分网络 EquiNet),EquiVSet 的性能平均提升 39%,说明了显式建模集合函数的重要性。
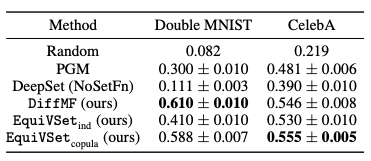
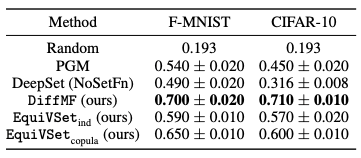
2. 在异常检测任务中,我们使用四个经典数据集:double mnist,celebA,fashion-mnist 和 cifar-10。下图给出了 celebA 上异常检测的例子。
图 3 celebA 数据集。每一行是一个数据样本。在每个样本中,正常图片拥有两个共同属性(最右列),异常图片(红色方框)没有该属性。
以下表格提供不同方法在该任务上的性能对比,可以看出 EquiVSet 显著优于其他方法, 并比 PGM 和 DeepSet(NoSetFn) 的性能分别平均提高 37% 和 80%。
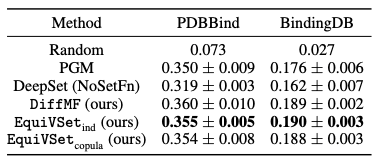
3. 在分子筛选中,我们使用 PDBBind 和 BindingDB 两个经典数据。该任务是从给定的分子库中,筛选出符合一定属性的分子。下表是 EquiVSet 和各个方法的对比结果。
四、结论
本文提出的基于最优子集的集合函数学习方法。通过将集合概率定义成能量模型,使得模型满足置换不变性、最小先验等特点。借助最大似然方法和等变变分技巧,模型能够高效地训练和推理。在商品推荐、异常检测和分子筛选上的应用认证了该方法的有效性。
© THE END
转载请联系本公众号获得授权
投稿或寻求报道:content@jiqizhixin.com