CVPR 2022 Oral | 基于熵筛选的半监督三维旋转回归

使用深度神经网络从单帧 RGB 图像中回归物体的三自由度旋转（朝向）是物体位姿估计、机器人抓取、三维重建等应用的关键技术之一，受到计算机视觉和计算机图形学的广泛关注。尽管近年来旋转回归领域的监督学习取得了明显的进展，这些工作大都依赖大规模有标注数据集。众所周知，三维旋转的精确标注是非常昂贵和耗时的，这一因素已经成为了制约该项技术发展的瓶颈之一。为了减少所需的标注，我们因而考虑探索半监督学习。当前半监督学习领域的工作主要关注分类问题，对回归关注不足，特别是对于旋转回归而言一片空白。注意到这样的算法需要处理 SO(3) 群这种非欧几里得流形上的元素预测并施加半监督学习，这对已有的半监督学习算法提出了严峻的挑战，也带来了可以研究的空间。

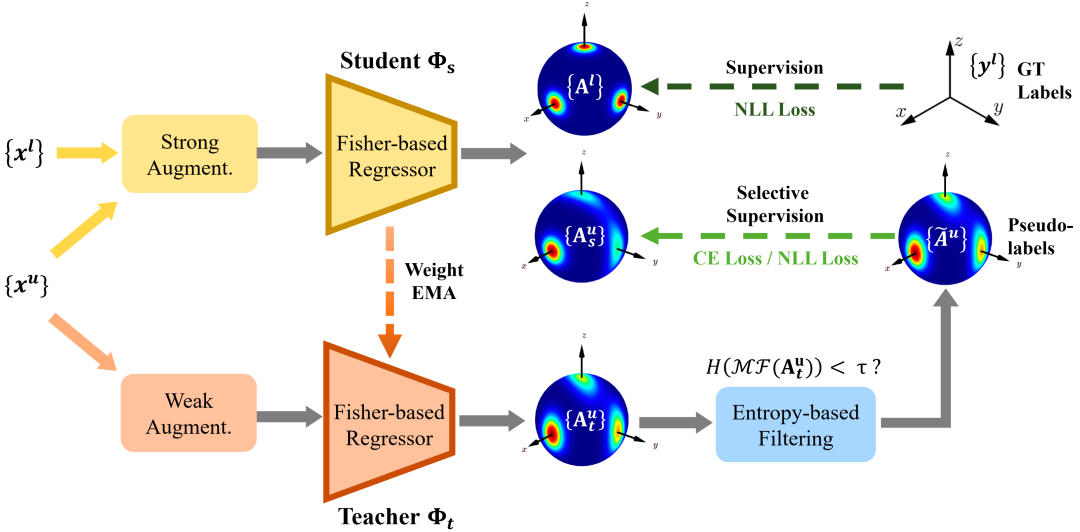
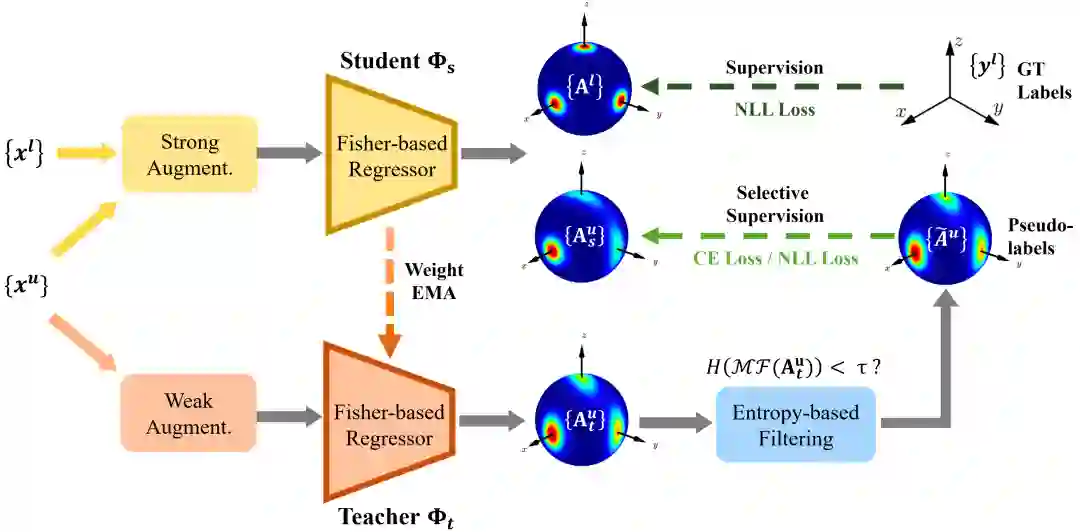
这此项工作中，我们首次提出了一个针对三维旋转回归的一般性的半监督学习算法 FisherMatch。该算法不局限于特定领域的知识，也不要求同一物体不同视角的图像对。借鉴在图像分类任务中广泛使用的半监督学习算法 FixMatch [1]，我们采用师生共同学习框架，其中学生模型的参数是可学习的，而老师模型的参数是学生模型参数的指数移动平均数（exponential moving average）。有标注数据和其对应真值用于训练学生模型，而无标注数据则使用由老师模型输出的“伪标签”进行监督，因而构建了师生模型之间的历史一致性。

FixMatch 成功的关键在于过滤掉置信度较低的伪标签，而仅使用高置信度的伪标签监督模型。这里的基本假设是预测结果的置信度和其质量呈正相关关系，因而基于置信度的筛选机制确保了伪标签的质量。幸运的是，分类任务输出的类别概率值天然包含了置信度信息；类似地，在三维目标检测任务中，3DIoUMatch [2] 构建了单独的网络用于预测当前输出的置信度。然而，由于缺乏对结果置信度的合理估计，将 FixMatch 应用到三维旋转回归任务中十分困难——我们既不能像分类任务一样直接依据概率值的大小作为置信度，也不能像三维目标检测任务一样产生足量对置信度的监督，但是我们依旧需要置信度来支持伪标签的筛选。

正如 [3] 指出，对旋转空间的概率建模是获取旋转回归置信度的合理方法。为了适应 SO(3) 群的特点，研究者分别使用 Bingham 分布，matrix Fisher 分布等分布描述旋转空间，进而获得置信度信息，其中 matrix Fisher 分布由于旋转表示的连续性获得了更优的效果。

在本文中，输入单张 RGB 图像，算法将输出一个 matrix Fisher 分布的参数，进而构建 SO(3) 空间的分布。我们提出通过计算分布的熵表达预测的置信度，并用于伪标签筛选机制。具体来讲，只有高置信度，即熵小于阈值的伪标签才会通过筛选并用于监督模型。实验证明熵对预测结果的效果具有明显的表达作用，即使在标注数据很少（低至5%）的情况下，熵仍能高效表达预测的准确性。在物体三维旋转估计的常用数据集 ModelNet10-SO(3) 和 Pascal3D+ 数据集上，我们的算法在多种标注数据比例的设定下均取得了明显优于全监督和其他半监督基线算法的效果。