SIGIR2021 | 基于排序的推荐系统度量优化新视角
本文分享一篇SIGIR’21的推荐系统文章:基于排序的推荐系统度量优化新视角。

论文下载地址:https://arxiv.org/pdf/2106.02545.pdf
动机
直接优化信息检索常用指标已经成为设计基于排序的推荐系统的一种有前景的方式。现有的大多数方法认为直接优化评测所用指标会得到更好的性能。但是,另一部分研究认为这样一种假设存在问题。因此,本文中,作者针对优化指标的选取对于基于排序的推荐系统的性能影响进行研究。分别在pairwise和listwise learning to rank (LTR)场景下进行了大量的实验。通过四个数据集上的实验结果得到了以下观点:
-
使用同样的指标进行优化和评测基于排序的推荐系统并不总能得到最好的推荐性能。
-
基于RBP损失相较于其他评测指标总能获得最好的性能,RBP有望成为LTR推荐场景下可替代的损失。
-
基于RBP的listwise优化对于活跃用户性能提升大于非活跃用户。
方法
预备知识
假设用户数目为
,物品数目为
,
交互矩阵为
(本文考虑二元交互数据),任意一个用户
都有
个交互过的物品。本文采用矩阵分解模型作为推荐模型,其中用户和物品分别被隐因子矩阵
和
表示,其中
是隐因子维度。利用用户和物品的隐向量得到预测矩阵
,其中
代表用户
对物品
的预测分数。因此排序位置
为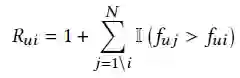
度量方式
在详细描述算法之前,介绍信息检索中常用的四个评测指标:RR, nDCG, RBP, AP,定义如下: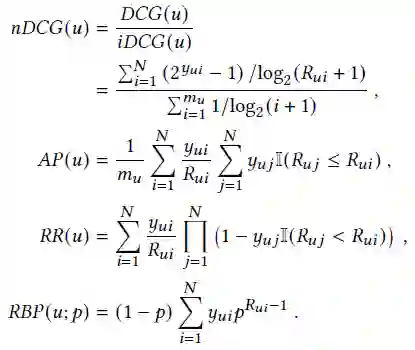
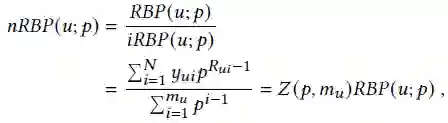
成对度量优化
对于pairwise指标优化方式,作者选择LambdaRank [1] 作为排序模型。对于RR, AP和nDCG的 优化,参考方法 [2],而使用LambdaRank优化RBP的方法之前从未有过,因此本文中详细介绍。
给定一个用户
,
优化一个物品对
的损失为: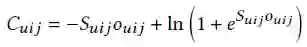

列表度量优化
pairwise方法可以轻松的避免优化指标的不平滑问题,但是在listwise方法中这一问题仍未被解决。能够成功解决这一问题十分重要是因为优化过程更加直观直接。评测指标难以优化的直接因素是因为指示函数的存在,为了统一对比,作者利用sigmoid函数替代指示函数。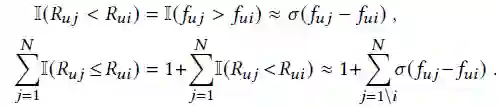
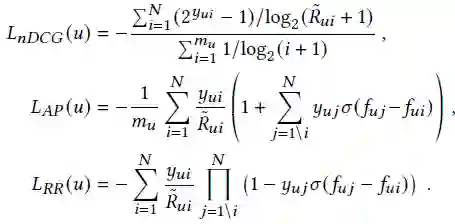
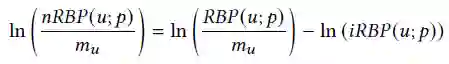
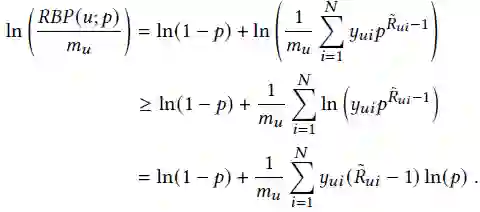
实验
数据集
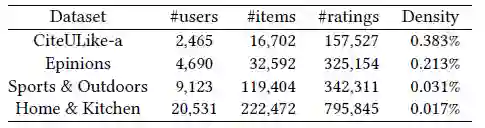
度量指标
𝑅𝑅, 𝐴𝑃, 𝑛𝐷𝐶𝐺 and 𝑅𝐵𝑃 with 𝑝 equal to 0.8, 0.9 and 0.95
结论
-
Should we Optimize the Metric Used to Evaluate?
根据上图结果可看出:1)当优化RR时性能较差,即便评测指标使用的也是RR,2)在pairwise的情况下,优化p=0.95的nRBP性能由于p=0.8/0.9的性能,3)优化nDCG,AP,nRBP性能差不多。
-
Is 𝑹𝑩𝑷 More Effective as Optimization Metric than Others?
通过上图显示,最好的pairwise和listwise性能都是在优化nRBP时得到。说明nRBP作为优化指标是有效的。
为了能够综合对比各个损失对于性能的影响,作者对比其Estimated Marginal Means (EMM)如上图所示:优化nRBP.95在六个评测指标上都实现了最好的性能,说明优化nRBP的优势。
另外,为了进一步探索在不同数据集上性能增益的稳定性,结果如下图所示:
-
When to Deploy 𝑹𝑩𝑷 for Recommendation? 1)在pairwise方法上,当有大量的活跃用户可用于训练时,优化nDCG和AP比优化nRBP.95更有优势,2)在listwise方法上,相比于nDCG和AP,在CiteULike数据集上优化nRBP.95使得所有用户都受益,在其他三个数据集上,对于非活跃用户的提升相差无几。
总结
作者报道了一项广泛的实验研究的结果,旨在获得有关此实践背后基础力量的新见解,并了解更多关于优化哪些指标以最大限度地提高推荐性能的信息。为此,作者扩展了通常用于定义 LTR 方法的目标函数的指标范围,并专注于 𝑅𝐵𝑃 作为其他指标(如 𝐴𝑃、𝑛𝐷𝐶𝐺 和 𝑅𝑅)的有前途的替代方案。
参考文献
[1] Christopher J. C. Burges, Robert Ragno, and Quoc Viet Le. 2006. Learning to Rank with Nonsmooth Cost Functions. In NIPS. MIT Press, 193–200.
[2] Pinar Donmez, Krysta M. Svore, and Christopher J. C. Burges. 2009. On the local optimality of LambdaRank. In SIGIR. ACM, 460–467.
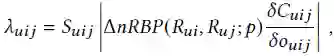
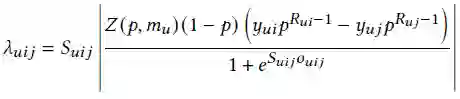
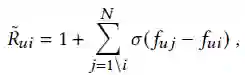
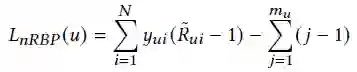
 根据上图结果可看出:1)当优化RR时性能较差,即便评测指标使用的也是RR,2)在pairwise的情况下,优化p=0.95的nRBP性能由于p=0.8/0.9的性能,3)优化nDCG,AP,nRBP性能差不多。
根据上图结果可看出:1)当优化RR时性能较差,即便评测指标使用的也是RR,2)在pairwise的情况下,优化p=0.95的nRBP性能由于p=0.8/0.9的性能,3)优化nDCG,AP,nRBP性能差不多。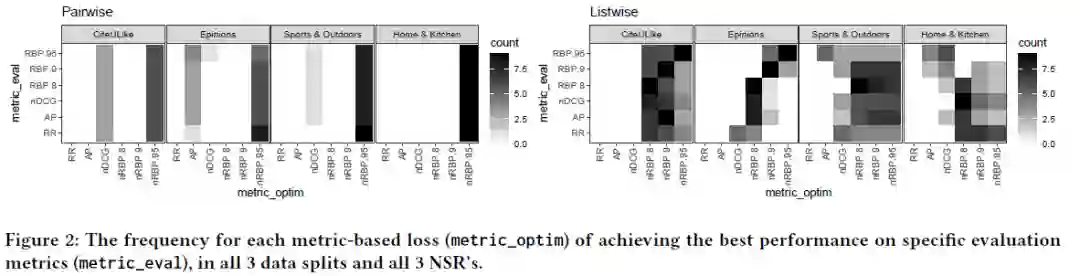 通过上图显示,最好的pairwise和listwise性能都是在优化nRBP时得到。说明nRBP作为优化指标是有效的。
通过上图显示,最好的pairwise和listwise性能都是在优化nRBP时得到。说明nRBP作为优化指标是有效的。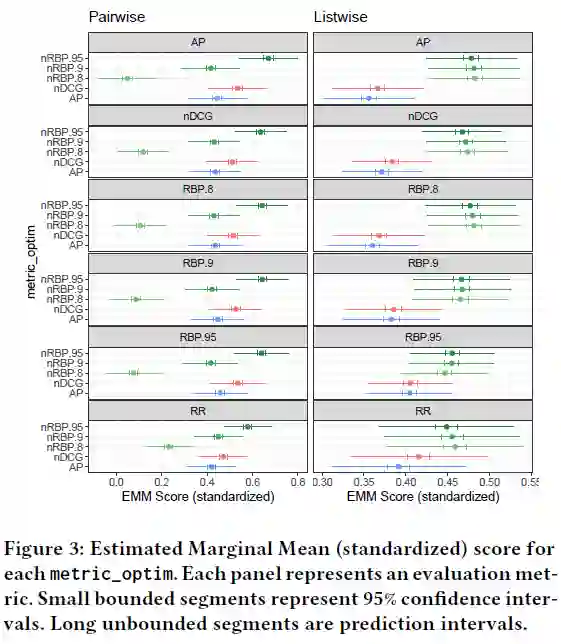 为了能够综合对比各个损失对于性能的影响,作者对比其Estimated Marginal Means (EMM)如上图所示:优化nRBP.95在六个评测指标上都实现了最好的性能,说明优化nRBP的优势。
为了能够综合对比各个损失对于性能的影响,作者对比其Estimated Marginal Means (EMM)如上图所示:优化nRBP.95在六个评测指标上都实现了最好的性能,说明优化nRBP的优势。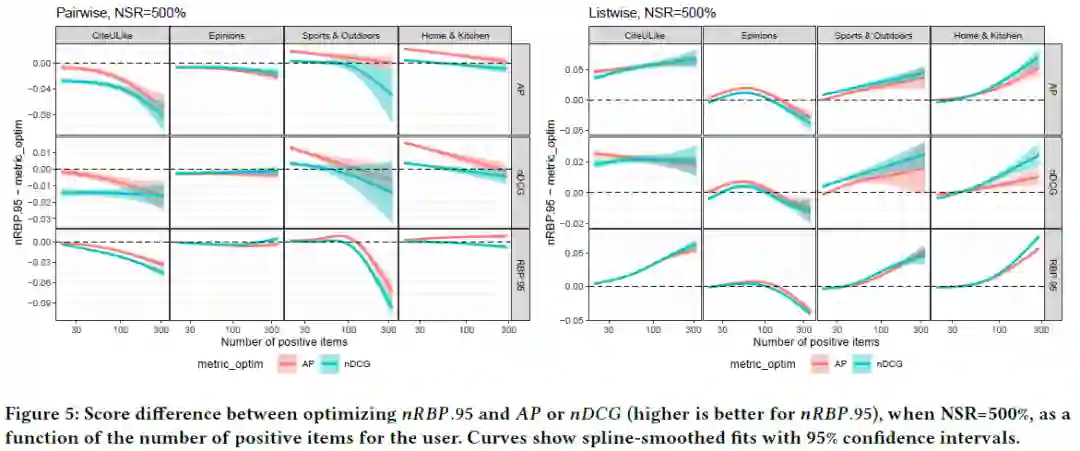 1)在pairwise方法上,当有大量的活跃用户可用于训练时,优化nDCG和AP比优化nRBP.95更有优势,2)在listwise方法上,相比于nDCG和AP,在CiteULike数据集上优化nRBP.95使得所有用户都受益,在其他三个数据集上,对于非活跃用户的提升相差无几。
1)在pairwise方法上,当有大量的活跃用户可用于训练时,优化nDCG和AP比优化nRBP.95更有优势,2)在listwise方法上,相比于nDCG和AP,在CiteULike数据集上优化nRBP.95使得所有用户都受益,在其他三个数据集上,对于非活跃用户的提升相差无几。





