ICLR'22 | You're AllSet! 超图GNN的新视角！

推荐一篇ICLR'22 新鲜出炉的超图GNN~

Title: You are AllSet: A Multiset Learning Framework for Hypergraph Neural Networks.

Authors: Eli Chien* (UIUC), Chao Pan* (UIUC), Jianhao Peng* (UIUC), Olgica Milenkovic (UIUC).

文章鏈結:

https://openreview.net/forum?id=hpBTIv2uy_E

代碼：

https://github.com/jianhao2016/AllSet

摘要

圖機器學習(特別是圖神經網絡)已經在許多圖相關任務取得成功，圖可以刻劃物件之間的 倆倆交互 關係，例如在社群網絡中，每個用戶為點(node)而朋友(或其他交互關係)為邊(edge)。但在現實問題中，我們也有許多非倆倆交互的關係，例如在共同作者網絡中，每個作者為點而論文為"邊"。可以注意到此處每個"邊"可能包含了 超過兩個點，這也就是所謂的超邊(hyperedge)，而這種廣義的圖則被稱作超圖(hypergraph)。

超圖透過CE轉換成一般圖

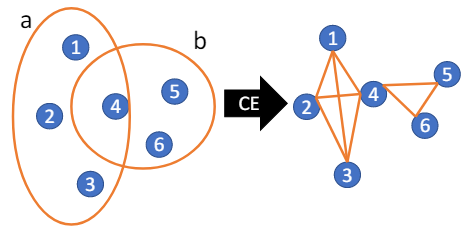
一個最直接處理超圖數據的方法就是透過集團擴張(clique-expansion, CE)轉換成一般的圖，之後便可以套用一般的圖神經網絡去處理。然而，此種轉換是會丟失信息的，進而於其他任務中造成算法次優的表現[Li et al. ICML 2018, Chien et al. AISTATS 2019]。因此，研究者們也提出了許多複雜但直接處理超圖的算法，例如多線性PageRank[Gleich et al. SIMAX 2015]與超圖上的 特徵問題有緊密的關係，[Tudisco et al. WWW 2021] 也於其工作中指出使用CE做標籤傳播的表現在某些情況下會比專門設計的非線性超圖標籤傳播要差。至此，有兩個重要的問題便自然浮現：

• 是否存在一統一框架可以包含CE、Z-based以及其他超圖傳播?
• 我們能否設計超圖神經網絡使其能根據數據學習不同且合適的超圖傳播？

本文中我們對兩者給出了肯定的答案。

AllSet 框架

AllSet 框架由兩個多重集函數 , 組成。此圖對應到前一張圖中的超圖。

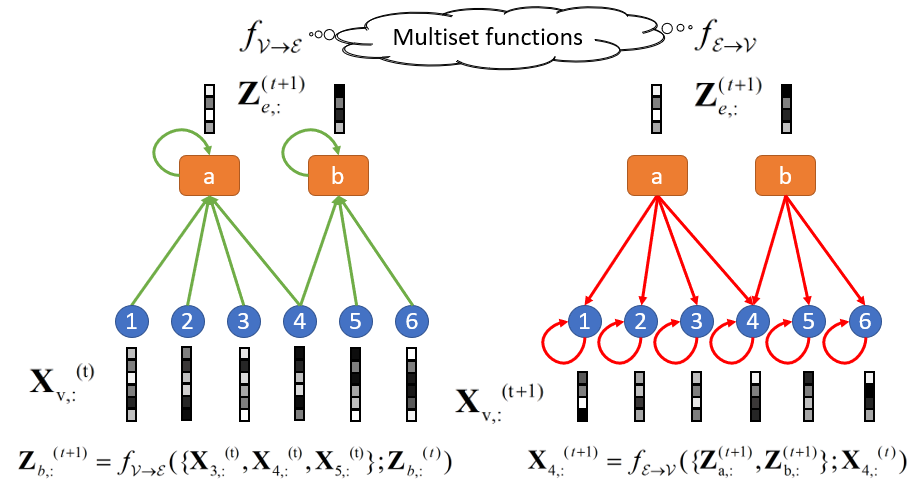
我們首先列出一些定義：一個超圖 包含了點集 與超邊集 。每個超邊 為點集的子集 ，為了方便起見我們也直接用 表示該超邊的編號。我們用 代表節點表示(representation)矩陣而 為關聯矩陣

最後，我們定義 為超邊 所對應的節點表示多重集。同理， 為節點 所對應的超邊表示多重集，且 為超邊表示矩陣。而我們的AllSet框架的傳播規則如下：

其中 , 為兩個多重集函數。注意，這裡我們也假設了 , 皆有完整的超圖拓譜信息 ，使其能還原度正則化(degree normalization)。

我們的理論貢獻如下：

• (Theorem 3.4) AllSet框架的表達能力(expressive power) 嚴格大於許多現有的超圖神經網絡，包含HGNN [Feng et al. AAAI 2019], HyperGCN [Yadati et al. NeurIPS 2019], HCHA [Bai et al. PR 2021], HyperSAGE [Arya et al. 2020], HNHN [Dong et al. 2020].
• (Theorem 3.3) CE-based 與 Z-based 傳播定義皆可被AllSet還原。
• (Theorem 3.5) AllSet是MPNN架構[Gilmer et al. ICML 2017]的超圖推廣。

值得一提的是，先前絕大部分的工作在設計超圖神經網絡時，還是基於類似圖卷積(graph convolution)的思想，也就是根據超圖定義下的拉普拉斯算子(Laplacian)來設計。其中HGNN與HCHA比較接近CE-based定義下的超圖拉普拉斯算子，如 。而HNHN與我們類似的定義了 與 的兩個傳播，但(粗略地說)只是將一般連接矩陣的角色替換成關聯矩陣。我們工作的創新性在於不去糾結該用何種超圖拉普拉斯算子定義傳播，而是將其看作兩個多重集函數，讓模型能自適應的去學習適合數據的傳播方式。

如何學習AllSet layer?

至此我們說明了AllSet框架的理論表達能力，但仍尚未說明如何學習兩個多重集函數 , 。根據我們AllSet的思想，我們必須確保模型為多重集函數的萬能模擬性質(universal approximation)。Deep Sets [Zaheer et al. NeurIPS 2017] 與 Set Transformer [Lee et al. ICML 2019]皆具有此一性質，因此為良好的選擇。我們將這些組合後得到的超圖神經網絡層分別稱為AllDeepSets 與 AllSetTransformer。

其中MH為多頭注意力機制(multihead attention)， 表示串聯(concatenation)，LN表示層正則化(layer normalization)。結合我們關於AllSet的理論結果，我們的AllSetTransformer 與 AllDeepSets的表達能力在理論上皆比現有的超圖神經網絡強。

實驗結果

我們將實驗重點放在節點分類任務上。除了五個常用的引用網絡數據集，我們也蒐集了另外三個較少使用的UCI數據集(Zoo, 20News, Mushroom)與兩個CV相關的數據集(NTU2012, ModelNet40)。另外，我們也新提出了三個超圖數據集(Yelp, House, Walmart)，且將許多現有的超圖神經網絡整合到我們的代碼中統一測試，有鑑於在超圖任務上尚未有像OGB的整合，我們的代碼與新數據可以看做對於超圖神經網絡測試基準化的第一步。

實驗結果。粗體灰底表示最佳表現，藍底表示在最佳表現一個標準差之内。

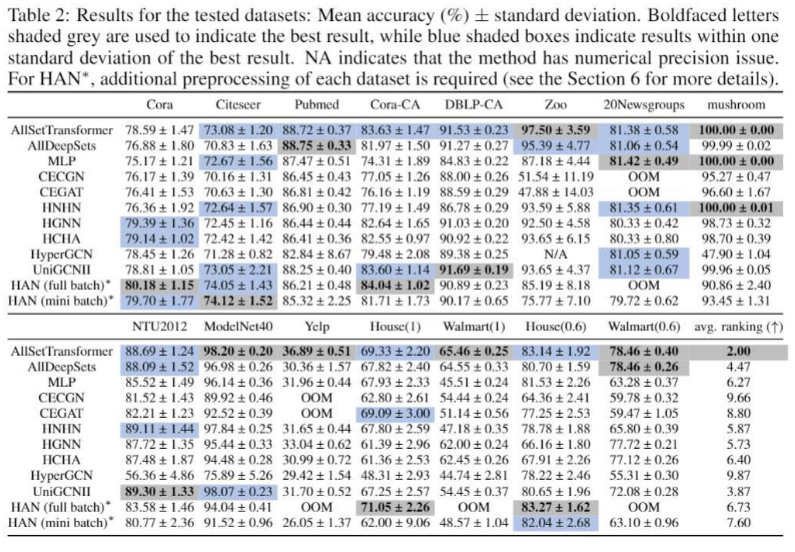
我們可以看到我們的AllSetTransformer總體來說表現最好，除cora外在6個數據集上取得最佳表現與在其餘的數據集與最佳模型表現相似。而其他模型都至少在兩個數據集上表現不佳。例如最強的基線(baseline)模型UniGCNII [Huang et al. 2021 IJCAI]在Yelp 以及Walmart上表現明顯差於AllSetTransformer。此一結果也凸顯的僅在基本的引用網絡數據集測試超圖神經網絡是不足的，我們必須增加更多不同的超圖數據集已確保超圖神經網絡的泛用性。

另外值得注意的是，雖然AllDeepSets與AllSetTransformer在理論上的表達能力相同，但如同Set Transformer作者提到，其注意力機制能幫助模型在現實中學習的更好，這點與我們的實驗結果也相吻合。

結論

我們針對超圖神經網絡提出了一個泛用的框架AllSet，我們證明了大部分現有超圖神經網絡層的表達能力皆嚴格弱於AllSet，且證明了AllSet為MPNN的超圖推廣。我們利用近年深層多重集函數學習的結果，結合AllSet概念設計出可學習的AllSet層AllSSetTransformer。我們的實驗顯示在節點分類任務中AllSetTransformer的表現優於SOTA超圖神經網絡，且我們也引入了新的超圖數據集，為超圖神經網絡的測試基準化做了初步的貢獻。