【上海交大ICLR2022】从因果不变性视角探讨图神经网络的分布外泛化鲁棒性

论文题目：Handling Distribution Shifts on Graphs: An Invariance Perspective

作者信息：吴齐天（上海交通大学），张恒瑞（伊利诺伊大学），严骏驰（上海交通大学），David Wipf（Amazon Web Service） 论文链接： https://www.zhuanzhi.ai/paper/536617e20409e65928e8540cc90c2db8

如何提高在新数据上的泛化性能是机器学习的一个核心问题。然而，近年来很多研究表明神经网络对数据的分布异常敏感，当测试数据的分布与训练数据呈现明显不同时，模型的泛化性能将受到很大的影响。这也为深度学习的实际应用与落地带来了隐忧与困难，特别是针对一些高风险的领域，如自动驾驶、金融投资、医疗诊断、刑事司法等。

目前大部分关于分布外泛化问题的研究集中在欧式数据（如图像、文本等），而对于图结构数据的相关研究还较少。与普通欧式数据不同的是，图结构数据上的分布偏移问题需要解决不同的技术挑战。首先，由于节点的互连特性，数据样本通常是非独立同分布的，这就为数据生成分布的建模带来了困难。其次，除了节点特征外，图的结构也蕴含了重要的信息，会影响到表示学习和预测任务。

本文介绍被International Conference on Learning Representations(ICLR‘22)会议接收的一项新工作，关注图结构数据的分布偏移问题，主要贡献如下：

• 对图上的分布外泛化问题给出了形式化定义，并提供了基于因果不变性假设的分析视角。
• 从理论上证明了传统学习方法无法实现有效的分布外泛化，并提出了一种新的目标函数（探索-外推风险最小化），用于实现从有限的观测数据向测试分布的外推。
• 通过理论分析表明新的目标函数可以有效解决分布外泛化问题，并且训练过程可以有效降低测试数据上的泛化误差。
• 为了验证提出的方法，考虑了三个不同的场景（处理人造混淆噪声、跨图迁移、动态图时序外推），并在多个不同的GNN主干模型上展示了方法的有效性和稳健性。

背景：图上的分布偏移与分布外泛化

宏观层面的定义 我们假设输入数据是一个图，它包含了两部分信息: 输入邻接矩阵和节点特征。这里表示节点的集合。此外，每个节点对应一个标签，所有节点的标签组成了一个向量。我们定义表示输入图的随机变量（是随机变量的一个具体实现），而是标签向量的随机变量（同理是一个具体实现）。此外，我们引入一个环境变量，它表示与数据生成相关联的某种上下文信息（未被观测到）。于是，图数据的生成过程可以由联合分布的展开进行描述

然而上述的定义方式不方便对图上的分布外泛化问题进行分析和求解，特别是考虑到图上的节点级任务（此时输入数据通常只有一张图或极少量的图），因此我们考虑一种微观层面的定义。

微观层面的定义 将输入的图以节点为单位（通常每个节点就是一个训练/测试样本）分解为一系列子图。具体的，假设表示节点的随机变量，定义节点的阶邻居内的节点集合为（这里是任意的正整数）。中的节点形成了一个子图，它包含了一个（局部）节点特征矩阵和一个（局部）邻接矩阵。同样定义为子图的随机变量而是其具体实现。定义是节点标签的随机变量，对应具体的实现。由此，我们将输入图分解为一系列子图的集合，这里我们可以将视为模型（例如图神经网络）的输入，是输出。注意到，这里可以视为是节点的马尔可夫毯（Markov Blanket），可以被分解为个独立相同的分布的乘积，即。基于上述定义，我们可以把观测数据从数据生成分布的采样生成过程考虑成两步：1)首先采样一个完整的输入图，而它可以被视作一系列子图的集合; 2)接着对图上的每一个单一节点，采样其标签。下面我们给出图上的分布外泛化问题的数学定义。

分布外泛化问题的形式化定义：给定训练数据（其数据分布为），模型的目标是最终泛化到新的测试数据（其数据分布为）。我们定义表示环境变量的取值集合，是模型的预测函数即，是损失函数。于是，我们的优化目标可以写为

当然，这里的第一步采样可以被省略，因为大部分图上的问题（如节点分类）通常假设只有一个输入图（包含成千上万的节点）。

方法：基于因果不变性的风险外推

直接解决上述的问题是非常困难的，因为模型在没有结构性假设和对学习任务的先验知识的情况下往往是不可能实现分布外泛化的。为此，本文从数据生成的角度，通过利用数据背后的因果不变性[1,2,3]，来引导模型学习到可以实现泛化的映射关系。

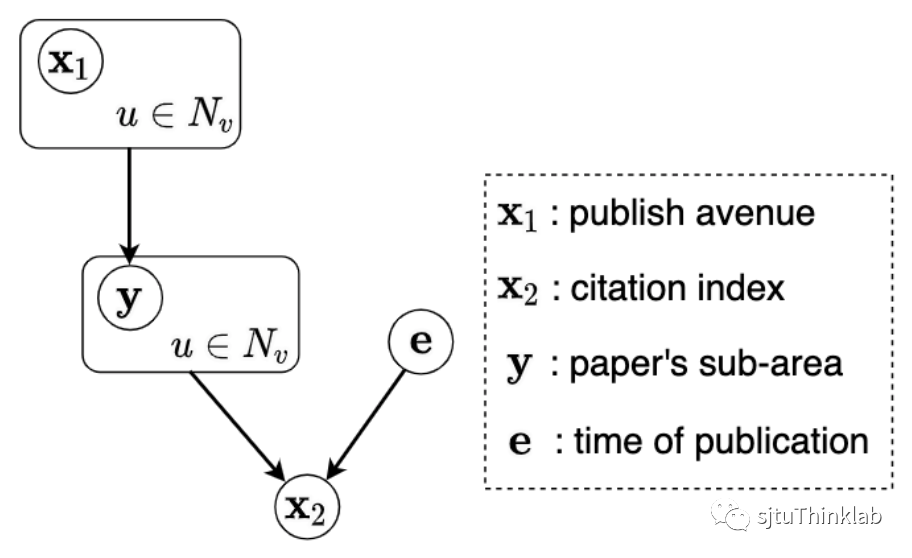
在进入技术细节之前，我们首先考虑一个具体的例子作为热身。我们考虑一个引用网络，每个节点表示一篇论文，每条连边表示论文之间的引用关系。每个节点有两个特征——论文发表的会议与论文的影响力，标签是论文的主题，环境是论文发表的时间。我们可以将上述变量的因果关系表示为下图：

具体的，对图中的三个因果依赖关系可以作如下理解。1）：论文发表的会议会决定论文研究的主题；2）：论文的影响力往往与论文的主题有关；3）：论文的影响力还与论文发表的时间有关（研究方向的流行度会随时间变化）。在这个例子中，会同时与和有关。也就是说，当环境发生变化时（对应于数据采样的分布发生了变化），与之间的关系也会发生变化。因此，如果模型在训练集上学习到了这部分关联性，当迁移到测试集后就不能获得令人满意的结果（因为环境的改变导致了与关系的改变）。相反的，如果模型在训练集中学习到了与的关系，就能够成功迁移到测试集（因为就算环境发生了改变，与之间的关系是稳定不变的）。

传统学习方法的局限性 我们接着把上述例子进行一般化推广，假设数据间的关系为线性且图神经网络只考虑一阶邻居。也就是说，（以及）只包含图上的一阶邻居。此外，假设每个节点有两个特征，，数据生成的过程假设如下：

这里和表示由独立的标准正态分布产生的噪声，是一个均值为零，方差大于零且与环境有关的随机变量。上面提到的引用网络的例子正是这个假设场景的具体体现。此外，我们考虑用于预测的图神经网络模型，其中都是需要学习的模型参数。可以看到，理想的最优模型参数是，此时GNN只利用了，即不受环境影响的特征。但是，我们可以证明，当直接使用传统的经验风险损失（Empirical Risk Minimization，即直接优化训练数据的损失）作为训练目标时，模型无法实现分布外泛化（一定会学习到与的关系）。

**命题1.**假设定义在与环境有关的数据上的误差损失为， 则当采用优化目标，模型训练得到的参数为，这里表示在不同环境下的方差。

这一结论表明，当我们直接使用传统的学习目标进行训练时，模型必然会学习到数据中对环境敏感的特征，从而无法实现理想的分布外泛化。与此同时，我们可以得到另一个结论。

命题2. 当采用优化目标时，模型对应的唯一最优解为。

这表明，我们可以同时最小化在不同环境的数据上的平均损失以及损失的方差，这就可以帮助模型学习到与环境无关的从输入特征到输出的关系，实现分布外泛化。

基于以上的探索和洞察，对于训练数据，我们可以考虑一个预测模型，将学习目标定义为在不同环境上对应风险损失的均值和方差：

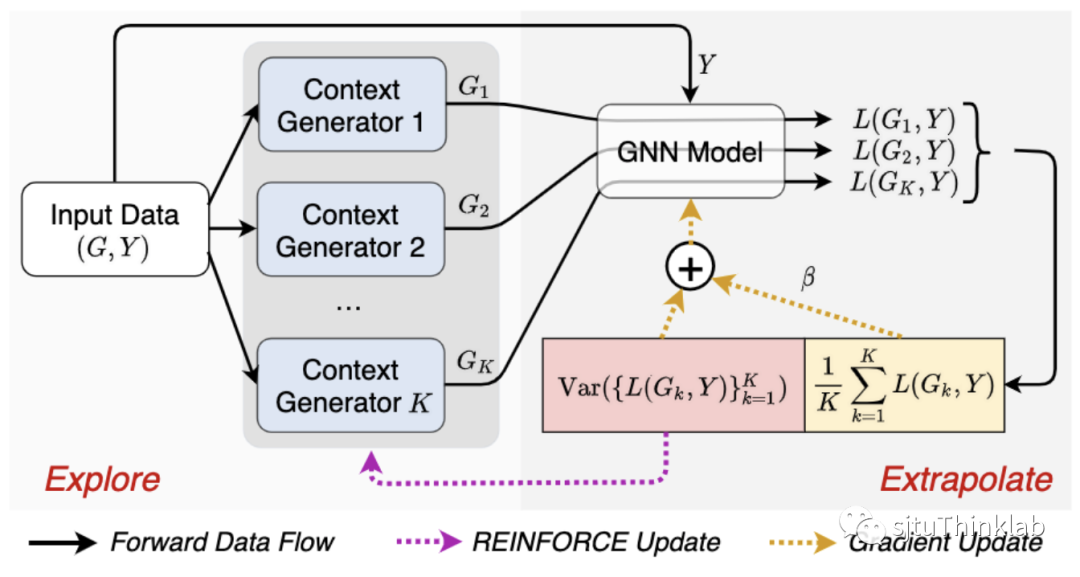
这里定义，是一个权重超参数。然而，上式则要求训练数据中包含来自多个环境的观测数据，并且数据样本与环境的对应关系也是已知的。对于图结构数据，尤其是节点级任务，这两个要求都是不满足的。通常情况下，训练数据只包含了一整张大图，即可以认为数据样本都来自同一环境。为了解决这一困难，我们引入个额外的数据生成器（），基于输入图生成份不同的图数据 来探索环境，模拟来自不同环境的观测数据。基于此，我们考虑如下的双层优化学习目标：

这里我们定义每个图数据所对应的损失函数。针对数据生成器，我们将其参数化为一个图结构学习器（graph editor），即将每一条连边假设为自由参数，对输入图进行局部改变（删除或增加连边）。具体的，我们将每一个改变视为动作（action），最终使用基于策略梯度的REINFORCE算法进行优化，以解决离散动作空间采样不可导的问题。我们将本文提出的方法称为Explore-to-Extrapolation Risk Minimization（EERM），下图给出了训练过程的数据流图。

理论分析

为了证明提出方法的有效性，下面我们进行理论分析，讨论学习目标产生的最优解与分布外泛化目标之间的关系，以及在训练数据上得到的模型在测试集上的泛化误差。为了提升阅读效率，在本节中我们使用概括性的语言取代部分数学符号和公式，具体的内容和证明请参见论文原文。首先，我们引入两个假设条件。

**假设1.**对于输入图数据中的任意子图，存在一个非线性映射由它给出的特征满足1) (不变性条件): ，以及2) (充分性条件): ，其中是一个非线性函数, 是独立的随机噪声。

**假设2.**对于满足假设1的数据，存在一个随机变量使得。我们假设在不同的环境下可以任意变化。 直观上讲，假设1保证了输入数据中存在一部分满足理想条件的预测信息，这部分信息可以充分预测标签而且这一关联对于不同环境是不变的。假设2保证了输入数据中还存在一部分对环境敏感的信息，随着环境的改变，它们与标签的关联性可以任意的变化。

**定理1.**在假设1与假设2的条件下，如果GNN模型产生的分布满足：1）不变性条件，即互信息 ，以及2）充分性条件，即被最大化，则学习目标(2)产生的预测函数对应(1)定义的分布外泛化问题的最优解。 这一结论表明，本文提出的方法可以在理论上保证取得理想的分布外泛化问题的最优解。此外，我们还可以从信息论的视角对测试分布上的泛化误差给出相应的分析。

**定理2.**只要模型输入与输出关于节点表示的条件互信息在训练集和测试集上是相等的，即，则对公式(2) 在训练数据上进行优化时，会降低测试集上预测分布与真实数据分布的距离的上界。 这一结论表明，只要模型给出的节点表示在训练集和测试集上具有相同的表达能力（具体量化为输入与输出包含在表示向量中的信息），本文的优化目标可以降低测试分布上的泛化误差上界。这进一步从理论上验证了提出方法的有效性。

实验结果

为了验证提出的方法，我们需要设计实验，测试模型在不同数据分布上的性能。真实的图数据中可能包含多种不同的分布偏移，这里我们考虑三种情况：人造混淆噪声（Artificial Transformation）、跨图领域迁移（Cross-Domain Transfer）、动态图时序泛化（Temporal Evolution）。下表展示了本文使用的6个数据集以及对应的分布偏移的形式。

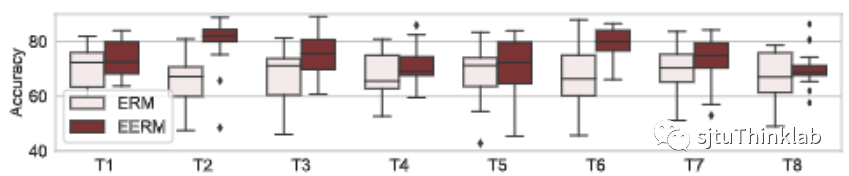
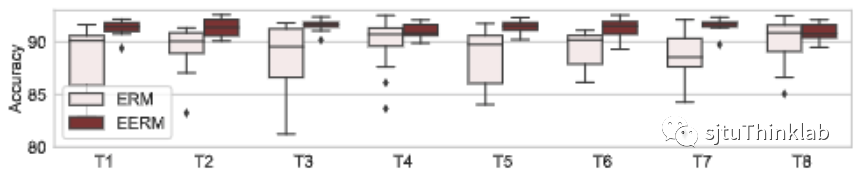
处理人造混淆噪声 我们首先考虑Cora和Amazon-Photo数据集，对其引入噪声，方法如下：采用两个随机初始化的GCN，第一个GCN基于原始节点特征生成节点真实标签，第二个GCN基于节点标签和环境id生成冗余特征，于是节点的特征为原始特征和冗余特征的拼接。对每个数据集，我们将环境id设为1-10，总共生成10张图，第一张用于训练，第二张验证，其余的作为测试。如此下来，训练集与测试集之间就被引入了分布偏移，原始特征与标签的关系是对于环境不变的，而冗余特征与标签的关系则是环境敏感的。我们考虑使用GCN作为预测模型主干，下图分别显示了使用传统方法（Empirical Risk Minimization，ERM，即直接优化训练数据的损失）与本文提出方法（EERM）在Cora和Amazon数据集上8个测试图的准确率（Accuracy）对比。这里，我们重复了20次实验（使用不同网络初始化），展示了准确率的分布情况。可以看到，EERM在绝大多数情况下明显好于ERM。

跨图领域迁移 一种典型的分布外泛化场景是图数据上的领域泛化（Domain Generalization）。这里我们考虑Twitch-Explicit和Facebook-100数据集，它们都是社交网络，分别包含了7张和100张子图。我们使用一部分图作为训练集，另一部分作为测试。由于每一张子图都是来自不同地区的社交网络，而且大小、密度、标签分布都不尽相同，因此训练数据与测试数据就天然存在分布偏移。

对于Twitch数据集，我们使用子图DE作为训练集，ENGB作为验证集，其余作为测试集。由于是二分类问题且类别标签不均衡，所以我们使用ROC-AUC作为评测指标。下图显示了分别使用GCN、GAT、GCNII作为网络主干，ERM与EERM在5个测试图上的性能对比。可以看到，EERM在几乎所有情况下都超越了ERM。

对于Facebook数据集，我们考虑使用多个图进行训练。具体的，我们考虑三种训练子图的组合。下表显示了使用不同训练子图的组合，在三个测试图（Penn，Brown，Texas）上的准确率对比。同样，EERM在绝大部分情况下超越了ERM，取得了最高7.2%的提升。

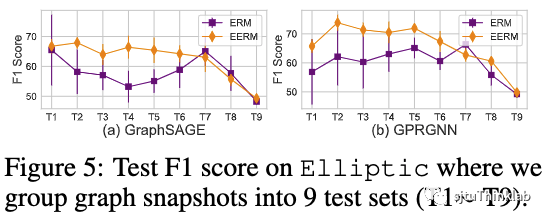
动态图时序外推 另一种典型的分布偏移来源于时序动态图，训练数据往往是历史某个阶段收集的片段，测试数据则来源于未来。随着时间的推移，图数据可能发生变化。这里我们进一步考虑两种不同的情况。第一种情况对应动态的时序snapshot，我们考虑Elliptic数据集，它一共包含49个graph snapshot，每一个记录了在一段时间内的金融交易，任务是识别网络中的非法节点。我们把snapshot按时间顺序排列，使用前5个作为训练，第6-10个作验证，其余的作为测试集（把每相邻的4个合并为一组）。我们使用F1分数作为评测指标，下图显示了使用GraphSAGE和GPRGNN作为主干模型的效果对比。可以看到，EERM显著好于ERM，取得了平均9.6%/10.0%的提升。

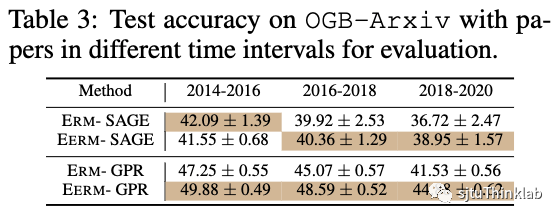
接着我们考虑第二种情况，随着时间的推移，图中的节点和连边会发生变化。这里我们考虑OGBN-Arxiv数据集，其中每个节点是论文。我们按论文的发表时间将节点分为训练集和测试集。为了引入分布偏移，我们扩大训练节点和测试节点的时间间隔：使用2011前发表的论文作为训练集，2011-2014年发表的论文作为验证集，2014年之后的为测试集。下表展示了时间在2014-2016/2016-2018/2018-2020年的测试节点上的测试准确率。可以看到，随着时间的推移（分布偏移进一步扩大），模型的性能都呈现下降趋势，但ERM的下降趋势更为明显。这也说明，EERM能够有效提升模型对分布偏移的鲁棒性。

讨论与总结

近期也有不少工作关注神经网络在图结构数据上的泛化性和鲁棒性，例如针对未知的特征/结构[6]和不同大小的图[7,8]。然而，他们主要专注于整图级别（graph-level）任务，而不能很好的解决节点级（node-level）任务。整图级别任务与节点级任务所关注的重点与技术难点是不同的。对于整图级别任务，每个输入图（如分子图）是一个预测对象，此时可以将输入图视为而图的标签视为。基于此，从同一环境里采样的观测数据可以视为独立同分布的数据样本，此时就可以直接使用一般的针对欧式数据的相关方法来处理分布外泛化的问题。相比之下，对于节点级任务，每个节点是需要预测的对象，他们被一张大图（如社交网络）所连接，节点之间的相互依赖使得样本是非独立同分布产生的，因此不能直接使用现有的方法来解决节点级任务的分布外泛化。本文作为此方向的第一个探索性工作，提出了一个新的视角来分析和解决节点级任务的分布外泛化问题。此外，本文的方法和理论也适用于整图级别的任务，甚至扩展到其他数据（如图像、文本），特别是处理从单一观测环境泛化到未知的测试环境。

除此之外，最近的一些研究工作探索了开放环境下的外推与泛化问题，例如对于输入空间的新特征[9]或未知用户节点[10]。本质上，这些工作同样考虑了分布外泛化问题，只不过这里的分布偏移来自于扩张的输入空间。另外，[9,10]所提出的方法利用了图神经网络作为一种显式的机制，实现利用已有实体的表示向量来推理计算新实体的表示向量。相比之下，本文的方法则对应一种隐式的机制，通过数据生成分布背后的不变性，来引导模型实现泛化与外推。 针对本文有任何疑问，或希望进一步讨论可以发送邮件至echo740@sjtu.edu.cn，或加微信myronwqt228。

参考文献

[1] Mateo Rojas-Carulla, Bernhard Schölkopf, Richard E. Turner, and Jonas Peters. Invariant models for causal transfer learning. Journal of Machine Learning Research, 2018. [2] Martín Arjovsky, Léon Bottou, Ishaan Gulrajani, and David Lopez-Paz. Invariant risk minimization. CoRR, abs/1907.02893, 2019. [3] Peter Bühlmann. Invariance, causality and robustness. CoRR, abs/1812.08233, 2018. [4] Keyulu Xu, Jingling Li, Mozhi Zhang, Simon S. Du, Ken-ichi Kawarabayashi, and Stefanie Jegelka. How neural networks extrapolate: From feedforward to graph neural networks. In ICLR, 2021. [5] Gilad Yehudai, Ethan Fetaya, Eli A. Meirom, Gal Chechik, and Haggai Maron. From local structures to size generalization in graph neural networks. In ICML, 2021. [6] Beatrice Bevilacqua, Yangze Zhou, and Bruno Ribeiro. Size-invariant graph representations for graph classification extrapolations. In ICML, 2021. [7] Qitian Wu, Chenxiao Yang, and Junchi Yan. Towards open-world feature extrapolation: An inductive graph learning approach. In NeurIPS, 2021. [8] Qitian Wu, Hengrui Zhang, Xiaofeng Gao, Junchi Yan, and Hongyuan Zha. Towards open-world recommendation: An inductive model-based collaborative filtering approach. In ICML, 2021.