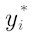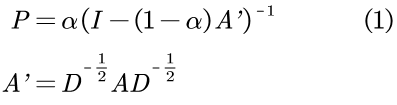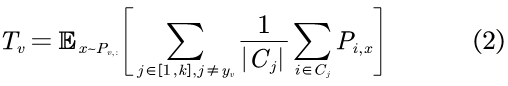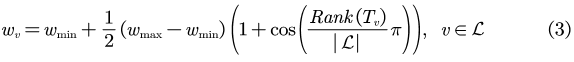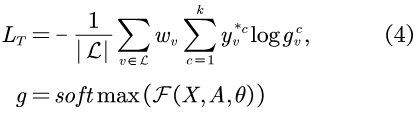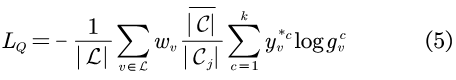NeurIPS 2021：半监督节点分类中的拓扑不平衡学习

Topology-Imbalance Learning for Semi-Supervised Node Classifification

NeurIPS 2021

01

—

研究背景

图作为一种被广泛使用的数据结构，近几年来受到越来越多的关注。与其他数据结构类似，图上节点分类的表征学习面临着节点类别数量不平衡的问题，即不同类别中样本数量可能存在很大的差异，由此可能会引起决策边界由多数类决定的问题。目前已有一些工作在研究数量不平衡的节点表征学习（简称QINL）。

然而，不同于其他数据结构，图结构数据还存在另外一个方面的不平衡问题：由标记节点的拓扑结构不对称、不均匀而导致的不平衡（即节点位置结构上的差异），可称作拓扑不平衡。而目前学术界缺乏对于拓扑不平衡相关问题的研究，本文希望通过研究拓扑不平衡的特点、危害及解决办法来引起学术界的重视。

02

—

拓扑不平衡

本文首次关注到图上拓扑不平衡节点表征学习（简称TINL），其主要关注由图中拓扑不平衡引起的决策边界漂移现象。与现有关注于QINL的工作相比，TINL研究的是由标记节点位置引起的不平衡，并有如下特点：

1.普遍性：由于图上节点的连接十分复杂，不同类别节点的拓扑结构自然是不对称的，从而使得TINL成为了节点表征学习的一个本质特征，也导致构造结构上完全平衡的数据集十分困难。

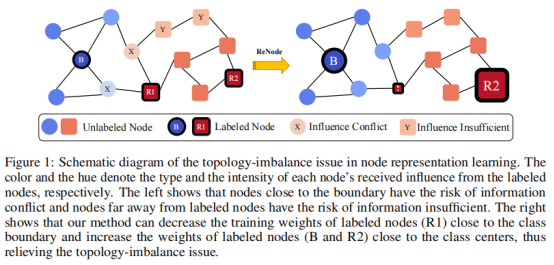
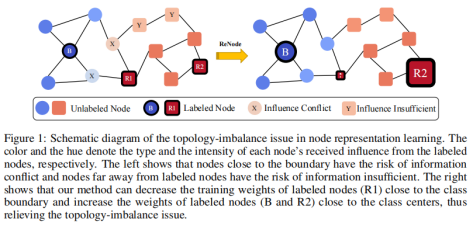
2.危害性：由于标记节点的影响会随着拓扑距离的增大而减小，故标记节点在不同类别中的拓扑结构不对称及在同一类别中的分布不均匀，就会分别导致信息冲突（靠近类边界的节点）以及信息不足（远离信息源的节点）的问题（如图1左侧所示），从而导致决策边界的漂移。

3.正交性：现有的QINL研究通常将同一类的标记节点视为一个整体，并基于每个类别的总数来设计解决方案，而TINL则关注于每个标记节点的位置对决策边界的影响，故现有的QINL方法无法直接直接应用于TINL中。

由于TINL的普遍性及危害性，对其进行研究对于节点表征学习具有重要意义，然而由于其正交性，现有的QINL方法无法应用于TINL问题。为了解决拓扑不平衡问题，从而增加节点分类性能，本文提出了一个训练框架ReNode，基于标记节点的拓扑位置对其进行重加权。本文设计了基于节点影响力冲突检测的拓扑结构相对位置（记作Totoro）度量，利用图中所有标记节点之间的交互来确定其拓扑位置。

基于Totoro，可进一步增加冲突小且可能靠近拓扑结构中心的节点训练权值，反之同理（具体如图1右侧所示）。

03

—

相关工作

3.1 标签传播

通过标签传播，可以更加直观地理解拓扑不平衡的本质。在标签传播（LP）中，标签从标记节点传播并沿边聚合，也可视为标签节点的随机游走过程。LP的预测结果q可以看作是标记节点影响力的分布（即节点主要受哪个类别的信息影响），而LP与GNN之间具有一致性（如图a所示），故节点影响力的边界可以有效反映GNN模型的决策边界。此外，节点影响为TINL和QINL提供了一个联合视图：理想情况下，节点影响的边界应与真实节点类别边界一致，然而标签节点数量不平衡（QINL）以及位置不平衡（TINL）都会导致节点影响的边界与真实边界发生偏移。

3.2 拓扑不平衡与数量不平衡

下图展示了图上两种不同的不平衡问题。其中图b展示了在随机采样情况下，图中同时存在数量不均衡和拓扑不平衡的问题，拥有更多节点的多数类（蓝色）由于数量优势将会获得更强的影响力，少数类（红色）同理则会获得更小的影响力，从而导致模型的决策边界（图中黄线）向少数类偏移。图c则展示了在类别数量均匀的情况下，少数类易于获得更多靠近类别边界的标记节点，从而导致决策边界向多数类移动。由下图可以看出，TINL与QINL共同引起了节点不平衡问题，而单独考虑两者中的一者则会影响对节点不平衡的学习。

04

—

Totoro

尽管节点拓扑结构的不平衡易于理解，然而对其进行量化并测量标记及节点的相对于其类别的拓扑位置则很难实现。由上文已知，拓扑不平衡会导致决策边界的偏移，故本文首先将拓扑不平衡问题抽象为标记节点到类别边界的距离，并设计了上文提到的基于节点影响力冲突检测的Totoro指标。与LP的公式类似，本文提出了一个个性化PageRank矩阵P以表示标记节点的影响力分布，表示为：

Totoro的基本思想在于：如果标注节点v在有着较大影响力的子图上遇到了影响力冲突，则认为v更加靠近类别边界。基于此思想，本文将节点v在全图上进行随机游走时，节点v与其他类别的标记节点之间的影响力冲突，作为衡量节点v拓扑位置的标准（即Totoro值），表示为：

y_v表示节v的ground-truth标签，P_v为节点v的个性化PageRank概率向量。Totoro值越大，则代表v更靠近类别边界，反之亦然。

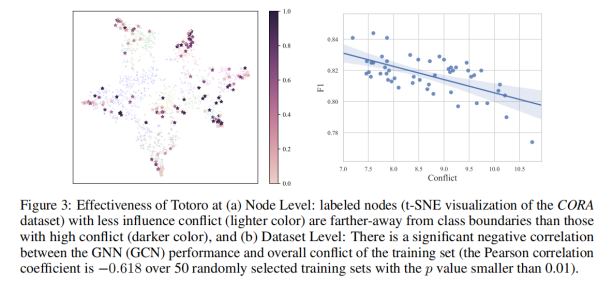
图3左展示了降维的图节点在二维上的分布，不同颜色代表不同类别，颜色越深表示节点更靠近边界。而右图则展示了标签集合整体的拓扑冲突水平和模型表现的关系，可以看出两者存在显著的相关关系，而Totoro可以有效反映图上的拓扑不平衡程度。

04

—

ReNode

考虑到TINL问题的普遍性，以及现有的GNN模型缺乏对其的考虑，故解决方案应兼容众多GNN模型，同时应和现有的QINL方法兼容，从而更加全面的解决图上不均衡问题。基于以上考虑，本文提出了ReNode框架如下图所示。ReNode的基本思想是提高距离拓扑中心较近的标记节点的训练权值，使其发挥更积极的作用，反之同理。

ReNode方法可具体表示为：

其中，w_max与w_min为超参，表示修改权值的上下界，Rank（T_v）表示T_v从小到大的排列顺序。数量平衡而拓扑不平衡情况下的损失L_T表示为：

F可表示任意的GNN编码器，g_i表示节点i在GNN中的输出，表示节点i单热向量中的金标签。

同理，类别数量及拓扑结构均不平衡情况下的损失 L _Q 可表示为：

05

—

实验

本文选用的数据集如下表所示：

并且分别在三个不同的场景中验证了ReNode方法的有效性。

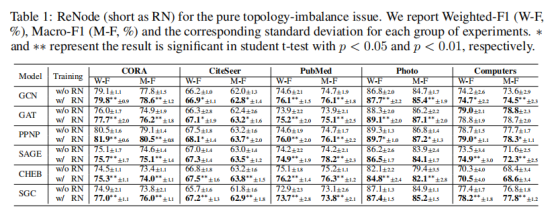
5.1 拓扑不平衡，数量平衡

选用GCN,GAT,PPNP,GRAPHSAGE,SGC,ChebGCN等常用GNN模型作为此部分实验的backbone模型。在cora等数据集上，ReNode方法均取得了较好的性能，说明本文方法能够有效缓解拓扑不均衡问题并提升模型效果。

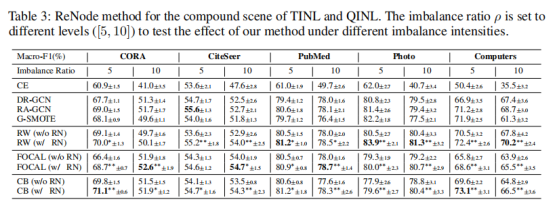
5.2 拓扑不平衡，数量也不平衡

在此项实验中，本文遵循其他QINL工作，将所有少数类定义为具有相同的标签尺寸n _i ，同时多数类有标签尺寸n _a =ρ*n _i ，ρ为不平衡率，区间为[5,10]。同时将最先进的QINL方法作为基线方法，GCN作为backbone模型。实验结果表明本文算法能够很好地与数量不平衡的方法相结合，从而更全面的解决图上不平衡的问题。
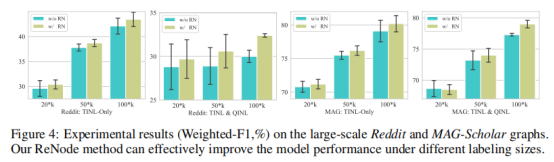
5.3在大规模图中的应用

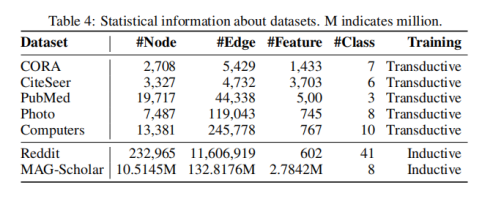
本文同样在社交网络Reddit以及引用网络MAG-Scholar（大规模图，有千万级别的节点），此处同样设置了上述两种情况。实验结果表明ReNode方法同样适用于超大图上的不平衡问题。

 

06

—

总结

本文首次关注到图上的拓扑不平衡节点表征学习（TINL）问题，并讨论了它存在的普遍性以及危害性。本文设计了一种基于冲突检测的度量方法Totoro来确定节点的拓扑位置，同时基于此度量，设计了一种调整节点权值的ReNode方法，大量的实验表明了本文方法的有效性。

点击原文链接可直接访问原论文。