必读的10篇 ICML 2019【图神经网络（GNN）】相关论文和代码

1、MixHop: Higher-Order Graph Convolutional Architectures via Sparsified Neighborhood Mixing（MixHop: 通过稀疏邻域混合实现的高阶图卷积结构）

作者：Sami Abu-El-Haija, Bryan Perozzi, Amol Kapoor, Nazanin Alipourfard, Kristina Lerman, Hrayr Harutyunyan, Greg Ver Steeg, Aram Galstyan

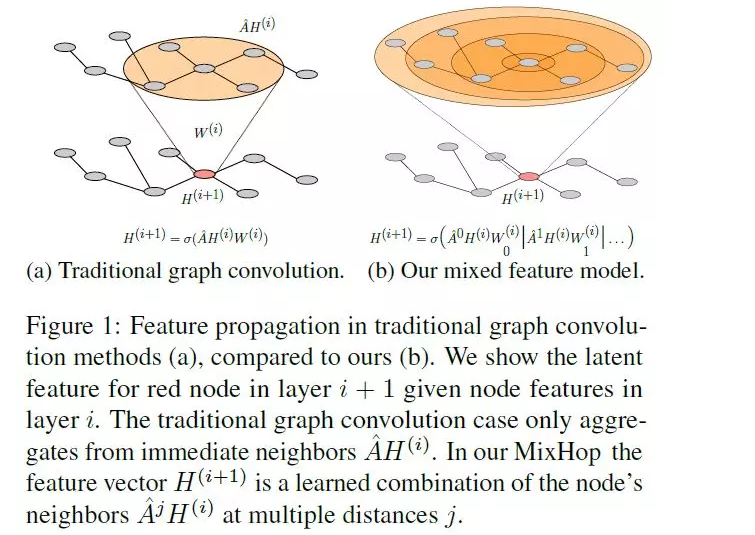
摘要：现有的基于图神经网络的半监督学习方法(如图卷积网络)不能学习一般的邻域混合关系。为了解决这个缺点，我们提出了一个新的模型，MixHop，它可以通过在不同距离重复混合邻居的特征表示来学习这些关系，包括不同的操作符。MixHop不需要额外的内存或计算复杂度，并且在一些具有挑战性的baseline上性能更好。此外，我们建议使用稀疏正则化，使我们能够可视化网络如何跨不同的图数据集对邻居信息进行优先级排序。我们对所学体系结构的分析表明，每个数据集的邻域混合是不同的。

网址：http://proceedings.mlr.press/v97/abu-el-haija19a.html

代码链接： https://github.com/samihaija/mixhop

2、Compositional Fairness Constraints for Graph Embeddings（图嵌入的组合公平性约束）

作者：Avishek Bose, William Hamilton

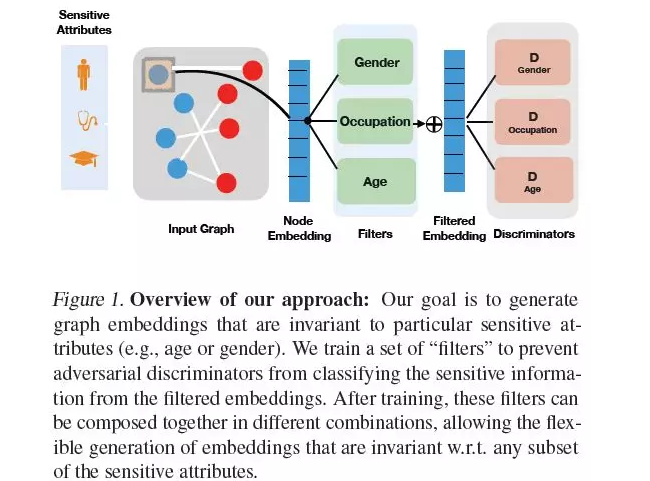
摘要：学习高质量的节点嵌入是基于图数据(如社交网络和推荐系统)的机器学习模型的关键步骤。然而，现有的图嵌入技术无法处理公平约束，例如，确保所学习的表示与某些属性(如年龄或性别)不相关。在这里，我们引入一个对抗框架来对图嵌入实施公平性约束。我们的方法是组合的，这意味着它可以灵活地适应推理过程中公平约束的不同组合。例如，在社会推荐的上下文中，我们的框架允许一个用户要求他们的推荐对他们的年龄和性别都是不变的，同时也允许另一个用户只对他们的年龄要求不变。在标准知识图和推荐系统基准测试上的实验突出了我们提出的框架的实用性。

网址：http://proceedings.mlr.press/v97/bose19a.html

代码链接： https://github.com/joeybose/Flexible-Fairness-Constraints

3、Learning Discrete Structures for Graph Neural Networks（学习图神经网络的离散结构）

作者：Luca Franceschi, Mathias Niepert, Massimiliano Pontil, Xiao He

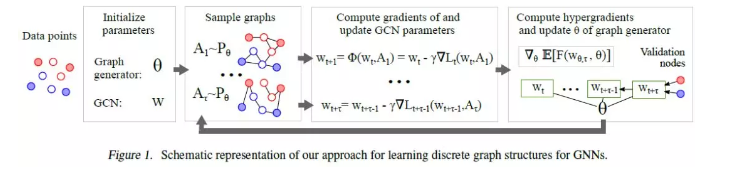
摘要：图神经网络(GNNs)是一种流行的机器学习模型，已成功地应用于一系列问题。它们的主要优势在于能够显式地合并数据点之间的稀疏和离散依赖结构。不幸的是，只有在这种图结构可用时才能使用GNN。然而，在实践中，真实世界中的图常常是嘈杂的、不完整的，或者根本就不可用。在此基础上，我们提出通过近似求解一个学习图边缘离散概率分布的双层程序来共同学习图卷积网络(GCNs)的图结构和参数。这不仅允许在给定图不完整或损坏的场景中应用GCNs，还允许在图不可用的场景中应用GCNs。我们进行了一系列的实验，分析了该方法的行为，并证明了它比相关的方法有显著的优势。

网址：http://proceedings.mlr.press/v97/franceschi19a.html

代码链接： https://github.com/lucfra/LDS

4、Graph U-Nets

作者：Hongyang Gao, Shuiwang Ji

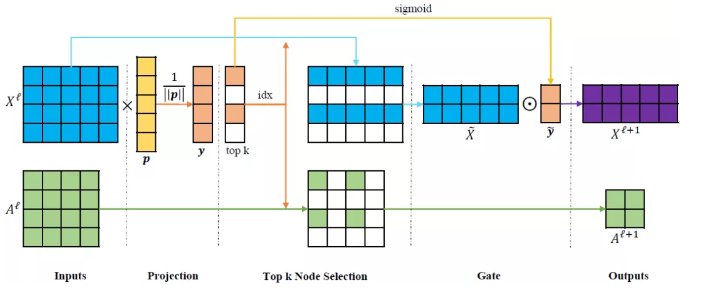
摘要：我们研究了图数据的表示学习问题。卷积神经网络可以很自然地对图像进行操作，但在处理图数据方面存在很大的挑战。由于图像是二维网格上节点图的特殊情况，图的嵌入任务与图像的分割等像素级预测任务具有天然的对应关系。虽然像U-Nets这样的编解码器结构已经成功地应用于许多图像的像素级预测任务，但是类似的方法在图数据上还是很缺乏。这是由于池化操作和上采样操作对图数据不是自然的。为了解决这些挑战，我们提出了新的图池化(gPool)和反池化(gUnpool)操作。gPool层根据节点在可训练投影向量上的标量投影值，自适应地选择节点，形成较小的图。我们进一步提出了gUnpool层作为gPool层的逆操作。gUnpool层使用在相应gPool层中选择的节点位置信息将图恢复到其原始结构。基于我们提出的gPool和gUnpool层，我们开发了一个基于图的编解码器模型，称为Graph U-Nets。我们在节点分类和图分类任务上的实验结果表明，我们的方法比以前的模型具有更好的性能。

网址：http://proceedings.mlr.press/v97/gao19a.html

代码链接： https://github.com/HongyangGao/gunet

5、Graph Neural Network for Music Score Data and Modeling Expressive Piano Performance（图神经网络用于乐谱数据和钢琴演奏表现力的建模）

作者：Dasaem Jeong, Taegyun Kwon, Yoojin Kim, Juhan Nam

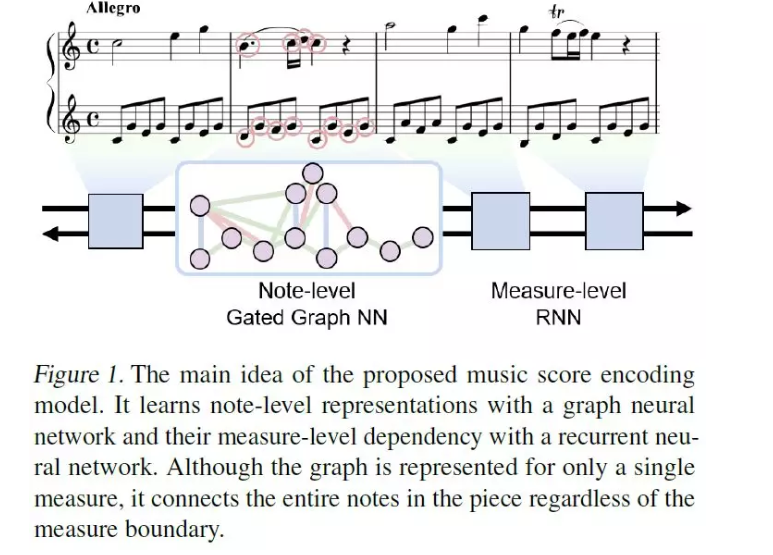
摘要：乐谱通常被处理为一维序列数据。与文本文档中的单词不同，乐谱中的音符可以由复调性质同时演奏，并且每个音符都有自己的持续时间。在本文中，我们使用图神经网络表示乐谱的独特形式，并将其应用于从乐谱中渲染表现力的钢琴演奏。具体地，我们设计了使用note-level门控图神经网络和采用迭代反馈方法的双向LSTM测量级层次注意网络的模型。此外，为了对给定输入分数的不同性能风格建模，我们使用了一个变分自编码器。听力测试结果表明，与baseline模型和层次注意网络模型相比，我们提出的模型生成了更多的类人性能，而层次注意网络模型将音乐得分处理为类词序列。

网址：http://proceedings.mlr.press/v97/jeong19a.html

代码链接： https://github.com/jdasam/virtuosoNet

6、Graph Matching Networks for Learning the Similarity of Graph Structured Objects（用于学习图结构物体相似性的图匹配网络）

作者：Yujia Li, Chenjie Gu, Thomas Dullien, Oriol Vinyals, Pushmeet Kohli

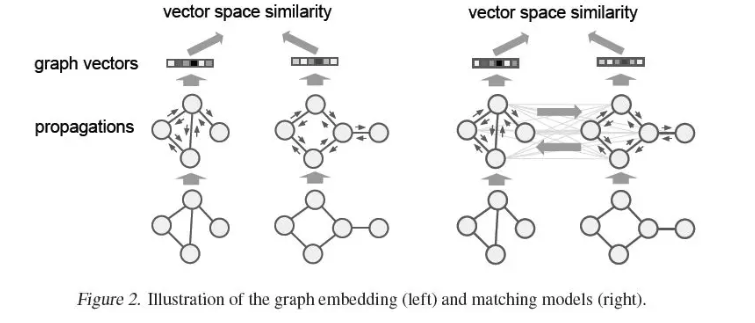
摘要：本文针对图结构物体的检索与匹配这一具有挑战性的问题，做了两个关键的贡献。首先，我们演示了如何训练图神经网络(GNN)在向量空间中嵌入图，从而实现高效的相似性推理。其次，提出了一种新的图匹配网络模型，该模型以一对图作为输入，通过一种新的基于注意力的交叉图匹配机制，对图对进行联合推理，计算出图对之间的相似度评分。我们证明了我们的模型在不同领域的有效性，包括具有挑战性的基于控制流图的功能相似性搜索问题，该问题在软件系统漏洞检测中发挥着重要作用。实验分析表明，我们的模型不仅能够在相似性学习的背景下利用结构，而且它们还比那些为这些问题精心手工设计的领域特定baseline系统表现得更好。

网址：http://proceedings.mlr.press/v97/li19d.html

7、Disentangled Graph Convolutional Networks（Disentangled图卷积网络）

作者：Jianxin Ma, Peng Cui, Kun Kuang, Xin Wang, Wenwu Zhu

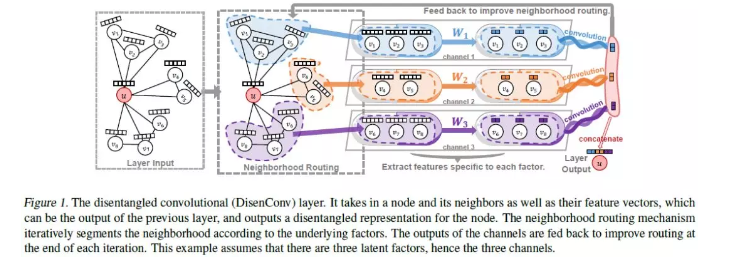
摘要：真实世界图形的形成通常来自于许多潜在因素之间高度复杂的交互作用。现有的基于图结构数据的深度学习方法忽略了潜在因素的纠缠，使得学习表示不鲁棒，难以解释。然而，在图神经网络的研究中，如何将潜在因素分解出来的学习表示方法面临着巨大的挑战，并且在很大程度上还没有得到探索。本文引入解纠缠（Disentangled）图卷积网络(DisenGCN)来学习disentangled节点表示。特别地，我们提出了一种新的邻域路由机制，它能够动态地识别可能导致节点与其相邻节点之间产生边的潜在因素，并相应地将相邻节点分配到一个提取和卷积特定于该因素的特性的信道。从理论上证明了该路由机制的收敛性。实验结果表明，我们提出的模型可以获得显著的性能提升，特别是当数据表明存在许多纠缠因素时。

网址：http://proceedings.mlr.press/v97/ma19a.html

8、GMNN: Graph Markov Neural Networks（GMNN: 图马尔可夫神经网络）

作者：Meng Qu, Yoshua Bengio, Jian Tang

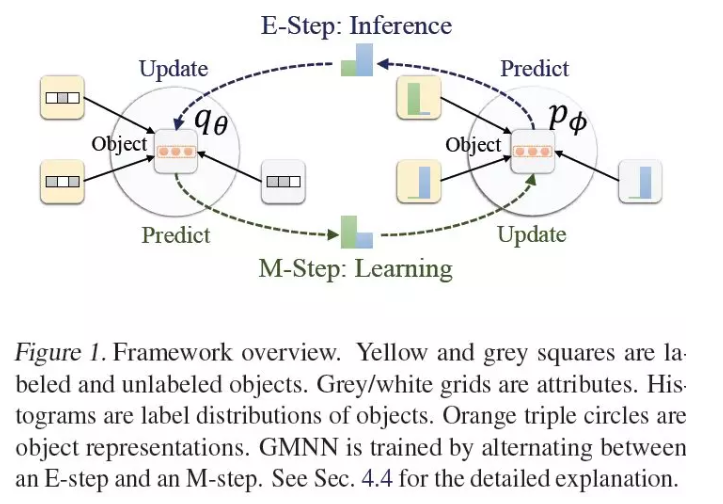
摘要：本文研究关系数据中的半监督对象分类问题，这是关系数据建模中的一个基本问题。在统计关系学习(如关系马尔可夫网络)和图神经网络(如图卷积网络)的文献中，这一问题得到了广泛的研究。统计关系学习方法可以通过条件随机场对对象标签的依赖关系进行有效的建模，用于集体分类，而图神经网络则通过端到端训练学习有效的对象表示来分类。在本文中，我们提出了一种集两种方法优点于一体的Graph Markov Neural Networks (GMNN)。GMNN利用条件随机场对目标标签的联合分布进行建模，利用变分EM算法对其进行有效训练。在E-step中，一个图神经网络学习有效的对象表示，逼近对象标签的后验分布。在M-step中，利用另一个图神经网络对局部标签依赖关系进行建模。在对象分类、链路分类和无监督节点表示学习等方面的实验表明，GMNN取得了较好的效果。

网址：http://proceedings.mlr.press/v97/qu19a.html

代码链接： https://github.com/DeepGraphLearning/GMNN

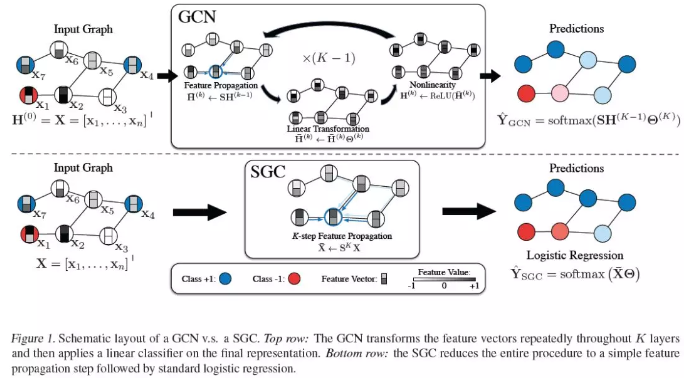
9、Simplifying Graph Convolutional Networks（简化图卷积网络）

作者：Felix Wu, Amauri Souza, Tianyi Zhang, Christopher Fifty, Tao Yu, Kilian Weinberger

摘要：图卷积网络(GCNs)及其变体得到了广泛的关注，已成为学习图表示的实际方法。GCNs的灵感主要来自最近的深度学习方法，因此可能会继承不必要的复杂性和冗余计算。在本文中，我们通过连续消除非线性和折叠连续层之间的权重矩阵来减少这种额外的复杂性。我们从理论上分析了得到的线性模型，结果表明它对应于一个固定的低通滤波器，然后是一个线性分类器。值得注意的是，我们的实验评估表明，这些简化不会对许多下游应用程序的准确性产生负面影响。此外，生成的模型可以扩展到更大的数据集，这是自然可解释的，并且比FastGCN的速度提高了两个数量级。

网址：http://proceedings.mlr.press/v97/wu19e.html

代码链接： https://github.com/Tiiiger/SGC

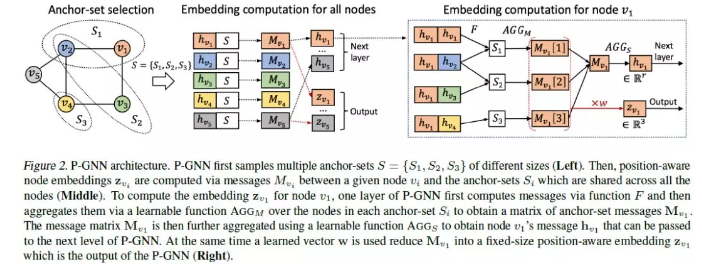
10、Position-aware Graph Neural Networks（位置感知图神经网络）

作者：Jiaxuan You, Rex Ying, Jure Leskovec

摘要：学习节点嵌入，捕捉节点在更广泛的图结构中的位置，对于图上的许多预测任务是至关重要的。然而，现有的图神经网络(GNN)结构在获取给定节点相对于图中所有其他节点的position/location方面的能力有限。本文提出了一种计算位置感知节点嵌入的新型神经网络—Position-aware Graph Neural Networks (P-GNNs)。P-GNN首先对锚节点集进行采样，计算给定目标节点到每个锚集的距离，然后学习锚集上的非线性距离加权聚集方案。通过这种方式，P-GNNs可以捕获节点相对于锚节点的位置。P-GNN有几个优点: 它们具有归纳性，可扩展性，并且可以包含节点特征信息。我们将P-GNNs应用于多个预测任务，包括链路预测和社区检测。我们显示，P-GNNs始终优于最先进的GNNs, 在ROC AUC分数方面提高了66％。

网址：http://proceedings.mlr.press/v97/you19b.html

代码链接： https://github.com/JiaxuanYou/P-GNN

论文下载

百度云链接：https://pan.baidu.com/s/1hOSkrDD2VWRJCTj9_uGrjw

提取码：vcc3