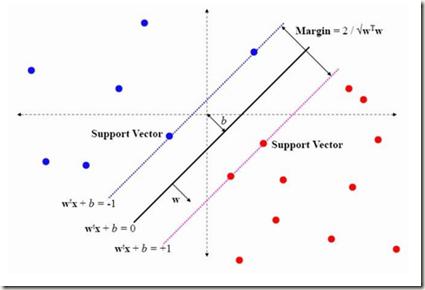
In this paper we consider the numerical solution to the soft-margin support vector machine optimization problem. This problem is typically solved using the SMO algorithm, given the high computational complexity of traditional optimization algorithms when dealing with large-scale kernel matrices. In this work, we propose employing an NFFT-accelerated matrix-vector product using an ANOVA decomposition for the feature space that is used within an interior point method for the overall optimization problem. As this method requires the solution of a linear system of saddle point form we suggest a preconditioning approach that is based on low-rank approximations of the kernel matrix together with a Krylov subspace solver. We compare the accuracy of the ANOVA-based kernel with the default LIBSVM implementation. We investigate the performance of the different preconditioners as well as the accuracy of the ANOVA kernel on several large-scale datasets.
翻译:暂无翻译