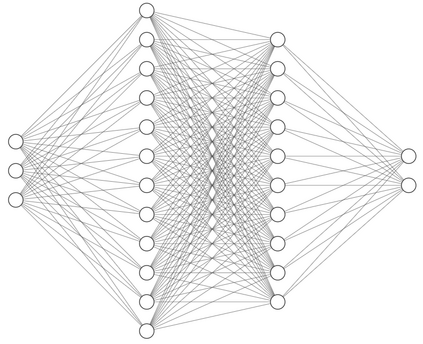
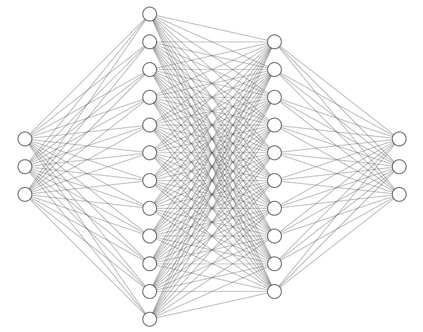
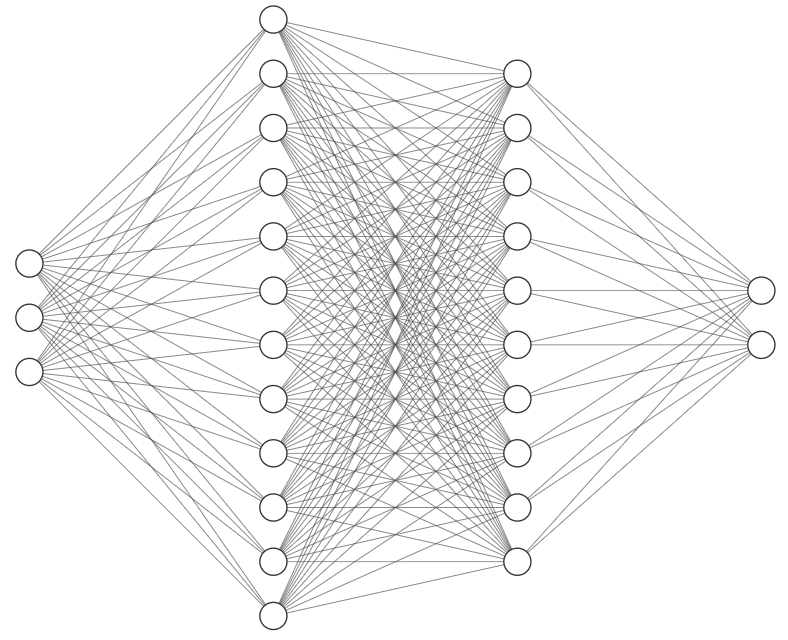
Fluid mechanics is a fundamental field in engineering and science. Solving the Navier-Stokes equation (NSE) is critical for understanding the behavior of fluids. However, the NSE is a complex partial differential equation that is difficult to solve, and classical numerical methods can be computationally expensive. In this paper, we present an innovative approach for solving the NSE using Physics Informed Neural Networks (PINN) and several novel techniques that improve their performance. The first model is based on an assumption that involves approximating the velocity component by employing the derivative of a stream function. This assumption serves to simplify the system and guarantees that the velocity adheres to the divergence-free equation. We also developed a second more flexible model that approximates the solution without any assumptions. The proposed models can effectively solve two-dimensional NSE. Moreover, we successfully applied the second model to solve the three-dimensional NSE. The results show that the models can efficiently and accurately solve the NSE in three dimensions. These approaches offer several advantages, including high trainability, flexibility, and efficiency.
翻译:----
EPINN-NSE: 用于求解 Navier-Stokes 方程的物理启发神经网络的增强版
流体力学是工程和科学中的基础领域。求解 Navier-Stokes 方程 (NSE) 对于理解流体行为是至关重要的。然而,NSE 是一个难以求解的复杂偏微分方程,传统的数值方法可能会有计算成本方面的问题。在本文中,我们提出了一种创新的方法,利用物理启发的神经网络 (PINN) 和若干改进性技术来解决 NSE。第一种模型基于近似假设,通过采用流函数的导数来近似速度分量。这种假设可用于简化系统,并确保速度符合无散条件。我们还开发了第二种更灵活的模型,可以在不做任何假设的情况下近似解。所提出模型可有效解决二维 NSE。此外,我们成功地将第二种模型应用于求解三维 NSE。结果表明,这些模型可以高效准确地解决三维 NSE。这些方法具有高可训练性、灵活性和效率等多个优点。